DE is a tangent to the circumcircle of ΔABC at the vertex A such that DE∣∣BC. If AB=17cm, then the length of AC is equal to
16.0cm
16.8cm
17.3cm
17cm
The correct Answer is:D
To solve the problem, we need to use the properties of parallel lines and angles in triangles. Here’s a step-by-step solution:
Step 1: Understand the configuration
We have a triangle ABC with a circumcircle. DE is a tangent to the circumcircle at point A, and DE is parallel to BC. We know that AB = 17 cm.
Step 2: Use the properties of parallel lines
Since DE is parallel to BC, we can use the Alternate Segment Theorem. This theorem states that the angle formed between a tangent and a chord through the point of contact is equal to the angle in the alternate segment.
Step 3: Set up the angles
Let’s denote:
- Angle DAB (the angle between the tangent DE and line AB) as θ.
- Angle ACB (the angle opposite to side AB in triangle ABC) as θ as well, since they are equal due to the Alternate Segment Theorem.
Step 4: Apply the property of triangles
From the properties of triangles, we know that if two angles are equal, the sides opposite to those angles are also equal. Therefore, we can conclude that:
- If angle DAB = angle ACB, then AB = AC.
Step 5: Substitute the known value
Since we know that AB = 17 cm, we can now state that:
- AC = AB = 17 cm.
Conclusion
Thus, the length of AC is equal to 17 cm.
Final Answer
AC = 17 cm.
---
We have a triangle ABC with a circumcircle. DE is a tangent to the circumcircle at point A, and DE is parallel to BC. We know that AB = 17 cm.
Since DE is parallel to BC, we can use the Alternate Segment Theorem. This theorem states that the angle formed between a tangent and a chord through the point of contact is equal to the angle in the alternate segment.
Let’s denote:
- Angle DAB (the angle between the tangent DE and line AB) as θ.
- Angle ACB (the angle opposite to side AB in triangle ABC) as θ as well, since they are equal due to the Alternate Segment Theorem.
From the properties of triangles, we know that if two angles are equal, the sides opposite to those angles are also equal. Therefore, we can conclude that:
- If angle DAB = angle ACB, then AB = AC.
Since we know that AB = 17 cm, we can now state that:
- AC = AB = 17 cm.
Thus, the length of AC is equal to 17 cm.
AC = 17 cm.
Topper's Solved these Questions
- GEOMETRYBOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XIV)
90 Videos
- GEOMETRYBOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - TRY YOURSELF
25 Videos
- GEOMETRYBOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XII)
90 Videos
- DISCOUNTBOOK - KIRAN PUBLICATIONCHAPTER - DISCOUNTEXERCISE - Test Yourself
10 Videos
- LCM AND HCF BOOK - KIRAN PUBLICATIONCHAPTER - LCM AND HCF EXERCISE - Test Yourself
18 Videos
Similar Questions
Knowledge Check
In a triangle ABC, angle bisector of ∠BAC cut the side BC at D and meet the circumcircle of ΔABC at E. If AC = 4 cm, AD = 5 cm, DE = 3 cm. Find the length of AB.
A10 cmB9.6 cmC12 cmD9 cmIn ΔABC,DE∣∣BCsuch that ADBD=35. If AC=5.6cm, then AE is equal to
A4.2 cm.B3.1 cm.C2.8 cm.D2.1 cm.The points D and E are taken on the sides ABandACof ΔABCsuch that AD=13AB,AE=13AC. If the length of BC is 15 cm, then the length of DE is :
A10 cmB8 cmC6 cmD5 cm
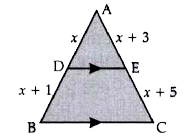
In ΔABC, DE || BC then the value of x is
View SolutionIn ΔABC, D and E are points on sides AB and AC respectively such that DE∣∣BC. If AE=1.8cm, BD= 7.2cm and CE= 5.4cm, then the length of AD is
View SolutionIn a triangle ABC, angle bisector of ∠BAC cut the side BC at D and meet the circumcircle of ΔABC at E. If AC = 4 cm, AD = 5 cm, DE = 3 cm. Find the length of AB.
View SolutionIn ΔABC,D and E are points on the sides AB and AC respectively ,such that DE||BC. If AD=2.5cm,BD=3cm and AE =3.75 cm , then the value of AC.
View SolutionIf in ΔABC,DE∣∣BC,AB=7.5cm,BD=6cm and DE=2cm, then the length of BC in cm is :
View Solution
