In the string mass system shown in the figure, the string is compressed by x0=mg2k from its natural length and block is relased from rest. Find the speed o the block when it passes through P (mg/4k distance from mean position)
_S01_030_Q01.png)
ω=√3km
x=Asin(ωt+ϕ)
v=Aωcos(ωt+ϕ)
at t=0,x=0
⇒ϕ=0
v=Aωcosωt
A=mg/2k
x=Asinωt
mg4k=mg2ksinωt
sinωt=12⇒ωt=π6⇒t=π6ω=T12
v=Aωcosωt
v=mg2k√3kmcos[√3km(2π√m3k/12)}=g√9m16k
Similar Questions
Find the maximum tension in the spring if initially spring at its natural length when block is released from rest.

View SolutionA block of mass m is attached to two unstretched springs of spring constants k1andk2 as shown in figure. The block is displaced towards right through a distance x and is released. Find the speed of the block as it passes through the mean position shown.

View SolutionA block of mass m is attached to two unstretched springs of springs constant k1 and k2 as shown in figure. The block is displaced towards right through a distance x and is released. Find the speed of the block as it passes through the mean position shown.

View SolutionA block of mass m is pushed against a spring of spring constant k fixed at the end to a wall. The block can side on a frictionless table as shown in figure. The natural length of the spring is L0 and it is compressed ti half its natural length when the block is relesed. Find teh velocity of the block aa s function of its distance x from the wall .

View Solution
A block of mass m is pushed against a spring of spring constant k fixed at one end to a wall.The block can slide on a frictionless table as shown in the figure. The natural length of the spring is L0 and it is compressed to one fourth of natural length and the block is released.Find its velocity as a function of its distance (x) from the wall and maximum velocity of the block. The block is not attached to the spring.
View SolutionA wheel of moment of inertia I and radius r is free to rotate about its centre as shown in figure. A string is wrapped over its rim and a block of mass m is attached to the free end of the string. The system is released from rest. Find the speed of the block as it descends through a height h.

View SolutionA block of mass m is hung vertically from an elastic thread of force constant mg/a. Initially the thread was at its natural length and the block is allowed to fall freely. Kinetic energy of the block when it passes through the equilibrium position will be
View SolutionA disc of mass m and radius r is free to rotate about its centre as shown in the figure. A string is wrapped over its rim and a block of mass m is attached to the free end of the string. The system is released from rest. The speed of the block as it descends through a height h, is :-

View SolutionFor the system shown in fig., initially the spring is compressed by a distance 'a' from its natural length and when released, it moves to a distance 'b' from its equillibrium position, the decrease in amplitude for half cycle (-a to +b) is :

View SolutionA spring mass systeam is shown in figure, spring is initially unstretched. A man starts pulling the block with constant force F. Find
(a) The amplitude and the time period of motion of the block
(b) The K.E. of the block at mean position
(c) The energy stored in the spring when the block passes through the mean position
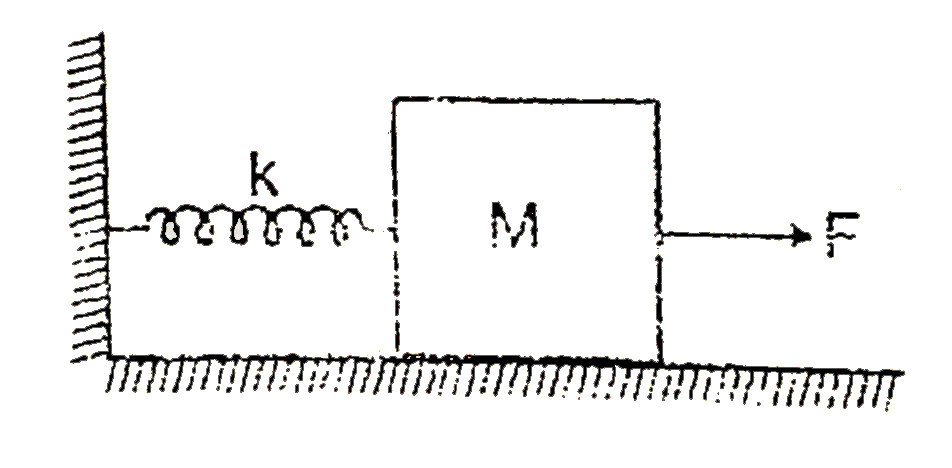
View Solution
