A block of mass m is hung vertically from an elastic thread of force constant mg/a. Initially the thread was at its natural length and the block is allowed to fall freely. Kinetic energy of the block when it passes through the equilibrium position will be
mga
mga2
zero
2mga
The correct Answer is:B
To solve the problem step by step, we will analyze the situation involving a block of mass m hung from an elastic thread with a force constant k=mga. We need to find the kinetic energy of the block when it passes through the equilibrium position after being released from rest.
1. Identify the Forces at Equilibrium:
At the equilibrium position, the forces acting on the block are:
- The weight of the block acting downwards: Fgravity=mg
- The restoring force of the elastic thread acting upwards: Fspring=kx
At equilibrium, these forces balance each other:
mg=kx
2. Substitute the Value of k:
Given that k=mga, we can substitute this into the equilibrium equation:
mg=(mga)x
3. Solve for x:
Rearranging the equation to solve for x:
x=a
This means the block stretches the elastic thread by a distance a when it reaches the equilibrium position.
4. Determine the Maximum Displacement (Amplitude):
Since the block is released from the natural length of the thread, the maximum displacement (amplitude) A from the natural length to the equilibrium position is:
A=a
5. Calculate the Angular Frequency ω:
The angular frequency ω for a mass-spring system is given by:
ω=√km
Substituting k=mga:
ω=√mgam=√ga
6. Find the Maximum Velocity Vmax:
The maximum velocity Vmax at the equilibrium position is given by:
Vmax=A⋅ω=a⋅√ga=√ag
7. Calculate the Kinetic Energy at Equilibrium Position:
The kinetic energy KE of the block when it passes through the equilibrium position is given by:
KE=12mV2max
Substituting Vmax=√ag:
KE=12m(√ag)2=12m(ag)=mga2
Final Answer:
The kinetic energy of the block when it passes through the equilibrium position is:
KE=mga2
At the equilibrium position, the forces acting on the block are:
- The weight of the block acting downwards: Fgravity=mg
- The restoring force of the elastic thread acting upwards: Fspring=kx
At equilibrium, these forces balance each other:
mg=kx
Given that k=mga, we can substitute this into the equilibrium equation:
mg=(mga)x
Rearranging the equation to solve for x:
x=a
This means the block stretches the elastic thread by a distance a when it reaches the equilibrium position.
Since the block is released from the natural length of the thread, the maximum displacement (amplitude) A from the natural length to the equilibrium position is:
A=a
The angular frequency ω for a mass-spring system is given by:
ω=√km
Substituting k=mga:
ω=√mgam=√ga
The maximum velocity Vmax at the equilibrium position is given by:
Vmax=A⋅ω=a⋅√ga=√ag
The kinetic energy KE of the block when it passes through the equilibrium position is given by:
KE=12mV2max
Substituting Vmax=√ag:
KE=12m(√ag)2=12m(ag)=mga2
The kinetic energy of the block when it passes through the equilibrium position is:
KE=mga2
Topper's Solved these Questions
- WORK, POWER AND ENERGYBOOK - DC PANDEYCHAPTER - WORK, POWER AND ENERGYEXERCISE - A Only One Option is Correct
42 Videos
- WORK, POWER AND ENERGYBOOK - DC PANDEYCHAPTER - WORK, POWER AND ENERGYEXERCISE - B More than One Option is Correct
26 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEYCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY
33 Videos
Similar Questions
A block of mass 'm' is attached to the light spring of force constant K and released when it is in its natural length. Find amplitude of subsequent oscillations.
View SolutionA block of mass m=2kg is connected to a a spring of force constant k=50N/m. Initially the block is at rest and tlhe spring has natural length. A constant force F=60N is applied horizontally towards, the maximum speed of the block (in m/s) will be (negelect friction).

View Solution
Knowledge Check
A block of mass m is attached to a spring of force constant k whose other end is fixed to a horizontal surface. Initially the spring is in its natural length and the block is released from rest. The average force acting on the surface by the spring till the instant when the block has zero acceleration for the first time is
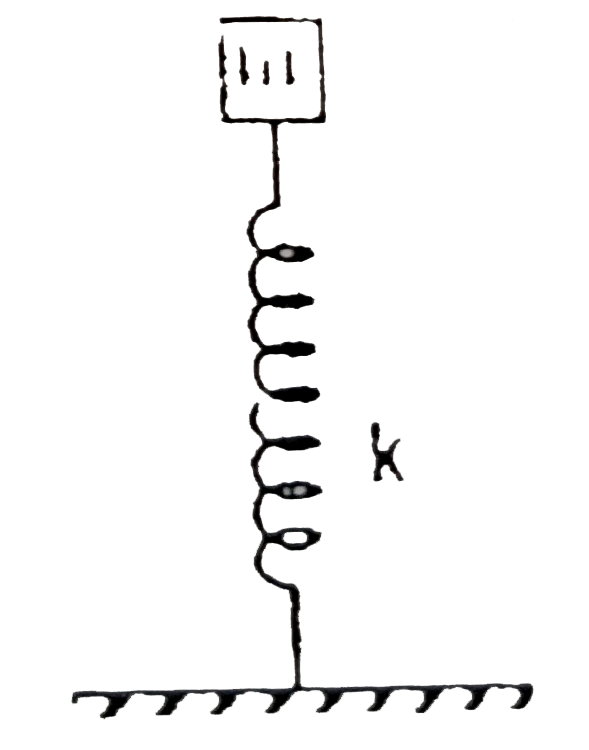 AmgπB2mgπC3mgπD4mgπ
AmgπB2mgπC3mgπD4mgπFind the maximum tension in the spring if initially spring at its natural length when block is released from rest.
 AmgBmg/2C3mg/2D2 mg
AmgBmg/2C3mg/2D2 mgA block of mass 5kg is initially at rest on a rough horizontal surface. A force of 45N acts over a distance of 2m. The force of friction acting on the block is 25N. The final kinetic energy of the block is
A40 JB90 JC50 JD140 J
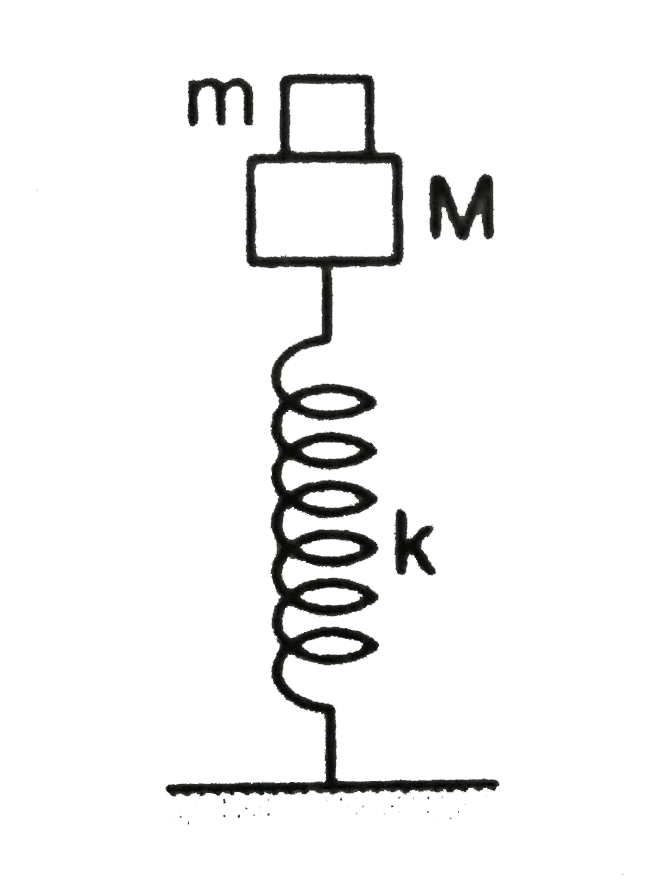
A small block of mass m is kept on a bigger block of mass M which is attached to a vertical spring of spring constant k as shown in the figure. The system oscilates verticaly. a.Find the resultant force on the smaller block when it is displaced through a distance x above its equilibrium position. b. find the normal force on the smaller blok at this position. When is this force smallest smaller block at this position. When is this force smallest in magnitude? c. What can be the maximum amplitude with which the two blocks may oscillate together?
View SolutionIn the string mass system shown in the figure, the string is compressed by x0=mg2k from its natural length and block is relased from rest. Find the speed o the block when it passes through P (mg/4k distance from mean position)
_S01_030_Q01.png)
View SolutionA block of mass m=2kg is connected to a spring of force constant k=50n/m. Initially the block is at rest and the spring has natural length . A constant force f=60N, is applied horizontally towards right, the maximum speed of the block (in m/s will be (neglect frication).

View SolutionA block of mass m = 2 kg is attached to two unstretched spring of force constant k1=100N/m and k2=125N/m
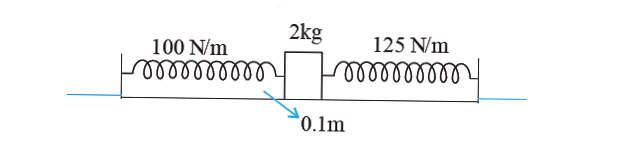
The block is displaced towards left through a distance of 10 cm and released. Find the speed of the block as it passes through the mean position.
View Solution
A block of mass m is attached to two unstretched springs of spring constant k, each as shown. The block is displaced towards right through a distance x and is released The speed of the block as it passes through the mean position will be
View Solution