
A block of mass m is pushed against a spring of spring constant k fixed at one end to a wall.The block can slide on a frictionless table as shown in the figure. The natural length of the spring is L0 and it is compressed to one fourth of natural length and the block is released.Find its velocity as a function of its distance (x) from the wall and maximum velocity of the block. The block is not attached to the spring.
12k(3L04)2=12mv2+12k(L0−x)2
when x<L0
⇒v=
⎷km[(3L04)2−(L0−x)2])<br>whenxgeL_0<br>velocityismaxiμmwhenx=L_0and<br>v_(max)==(3L_0)/(4)sqrt((k)/(m))
Topper's Solved these Questions
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - Single Correct Answer type
491 Videos
- CAPACITOR AND CAPACITANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Integer
5 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Single Answer Correct Type
22 Videos
Similar Questions
A block of mass m is pushed against a spring of spring constant k fixed at the end to a wall. The block can side on a frictionless table as shown in figure. The natural length of the spring is L0 and it is compressed ti half its natural length when the block is relesed. Find teh velocity of the block aa s function of its distance x from the wall .

View SolutionFind the maximum tension in the spring if initially spring at its natural length when block is released from rest.

View SolutionA block of mass m is connected to another .block of mass M by a massless spring of spring constant k. A constant force f starts action as shown in figure, then:

View SolutionA block of mass m is attached with a spring in vertical plane as shown in the figure. If initially spring is in its natural length and the block is released from rest, then maximum extension in the spring will be
View SolutionA block of mass 2kg is attached with a spring of spring constant 4000Nm−1 and the system is kept on smooth horizontal table. The other end of the spring is attached with a wall. Initially spring is stretched by 5cm from its natural position and the block is at rest. Now suddenly an impulse of 4kg−ms−1 is given to the block towards the wall.
Find the velocity of the block when spring acquires its natural length
View SolutionTwo springs, each of spring constant k, are attached to a block of mass m as shown in the figure. The block can slide smoothly alongs a horizontal platform clamped to the oppsite walls of the trolley of mass M. If the block is displaced by xcm and released, the period of oscillaion is :

View SolutionA block of mass m, attacted to a string of spring constant k, oscillates on a smooth horizontal table. The other end of the spring is fixed to a wall. The block has a speed v when the spring is at its natural length. Before coming to an instantaneous rest. If the block moves a distance x from the mean position, then
View SolutionThe block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

View SolutionA block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is μ then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
View SolutionA block of mass m compresses a spring iof stifffness k through a distacne l/2 as shown in the figure .If the block is not fixed to the spring the period of motion of the block is
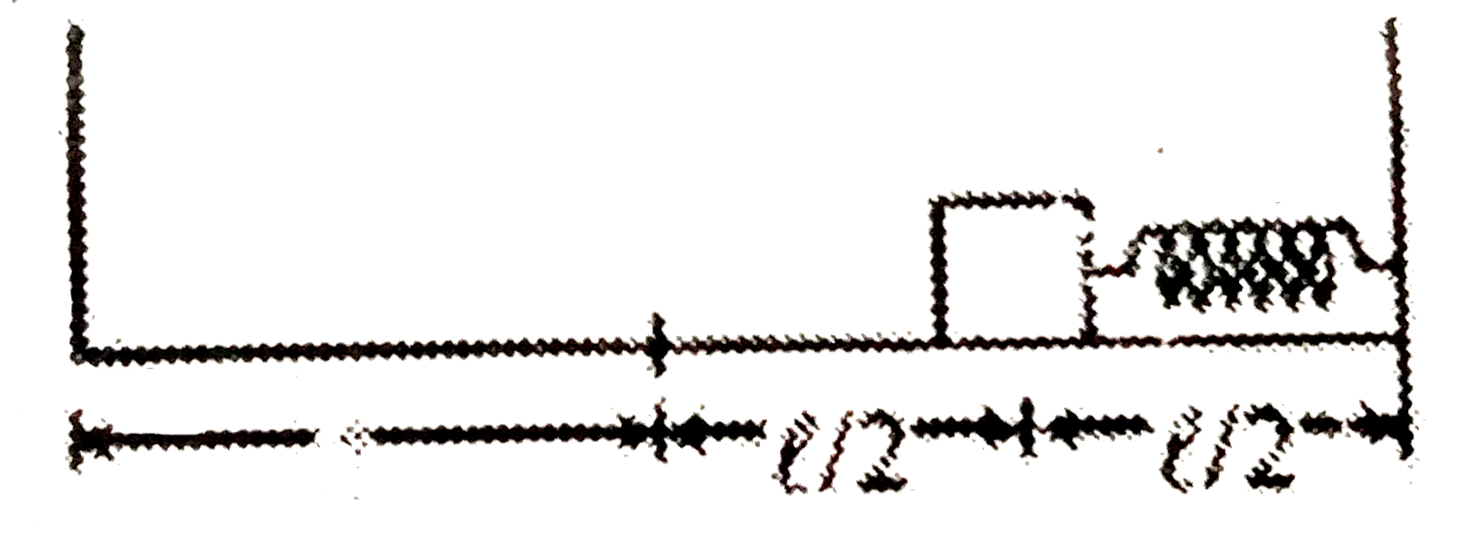
View Solution
