
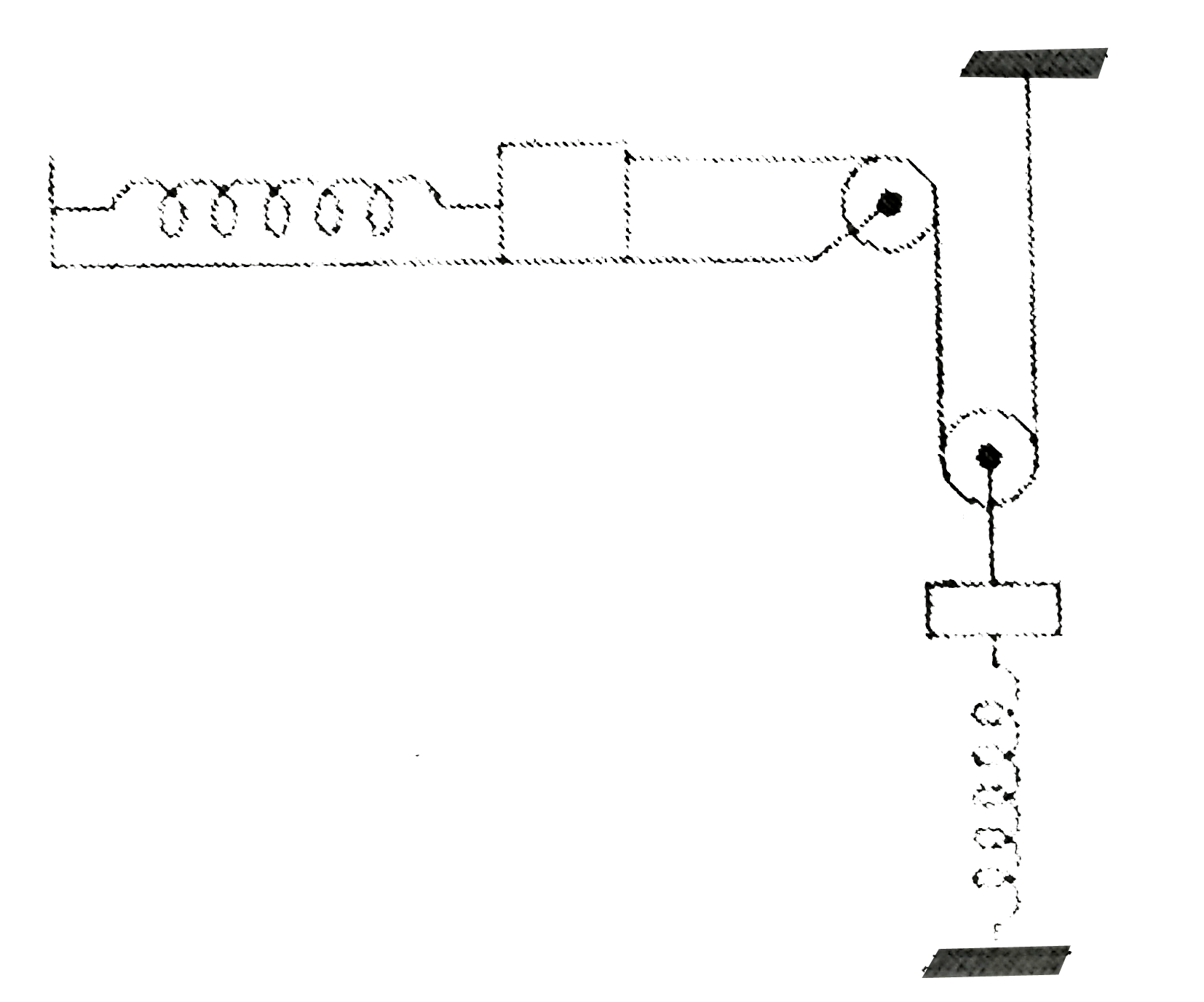
In an elevator a system is arranged as shown in figure. Initially elevator is at rest and the system is in equilibrium with middle spring unstretched. When the elevator accelerated upwards, it was found that for the new equilibrium position (with respect to lift), the further extension i the top spring is 1.5 times that of the further compression in the bottom spring, irrespective of the value of acceleration
(a) Find the value of in terms of spring constants for this happen.
(b) if and kg and acceleration of the elevator is , find the tension in the middle spring in the final equilibrium with respect to lift.




Let the initial extension in top string be and the compression in the botton string be respectively.
For equilibrium of
..(1)
m_2k_3x_3=m_2g=1.5yand compression in the middle spring IN the frame of lift
(a)
..(3)
..(4)
(m_1)/(m_2)=(3k_1+k_2)/(2k_3-k_2)k_1=k_2=k_3=500(N)/(m)m_1=2kga=2.5(m)/(s)y=(2xx2.5)/(2xx500)=(1)/(200)m=0.5cm=k(0.5y)=500xx(1)/(2)xx(1)/(2)xx10^-2T=1.25N
Topper's Solved these Questions
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - Single Correct Answer type
491 Videos
- CAPACITOR AND CAPACITANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Integer
5 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Single Answer Correct Type
22 Videos
Similar Questions
All surfaces shown in figure are smooth system is released with the spring unstretched In equilibrium, compression in the spring will be

View SolutionAll surfaces shown in figure are smooth system is released with the spring unstretched In equilibrium, compression in the spring will be

View SolutionConsider the situation shown in figure. Initially the spring is unstretched when the system is released from rest. Assuming no friction in the puley, find the maximum eleongation of the spring.
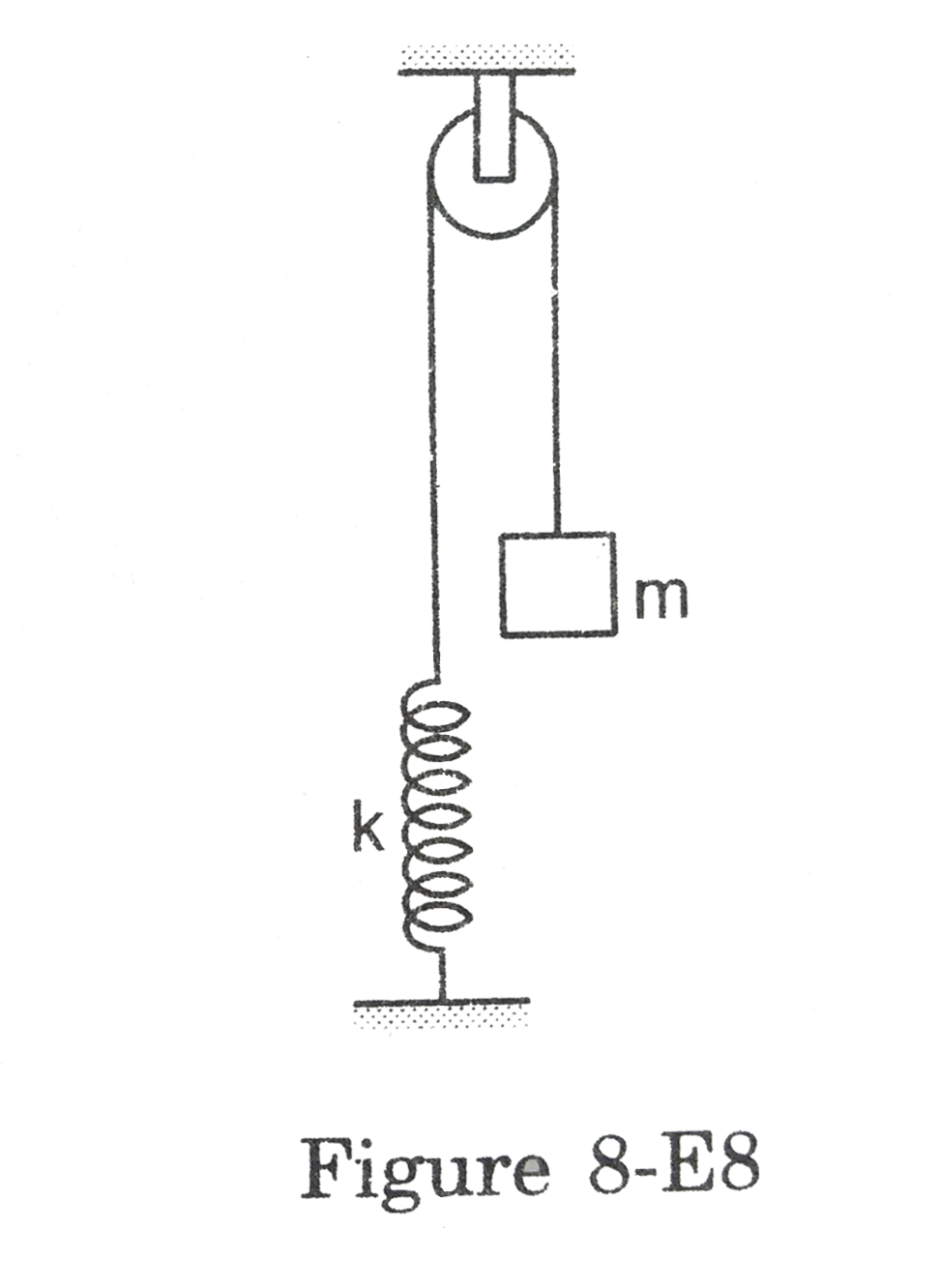
View SolutionA barometer kept in an elevator accelerating upward reads 76 cm. The air pressure in the elevator is
View SolutionBlocks A and B shown in the figure are having equal masses m. The system is released from rest with the spring unstretched. The string between A and ground is cut, when there is maximum extension in the spring. The acceleration of centre of mass of the two blocks at this instant is
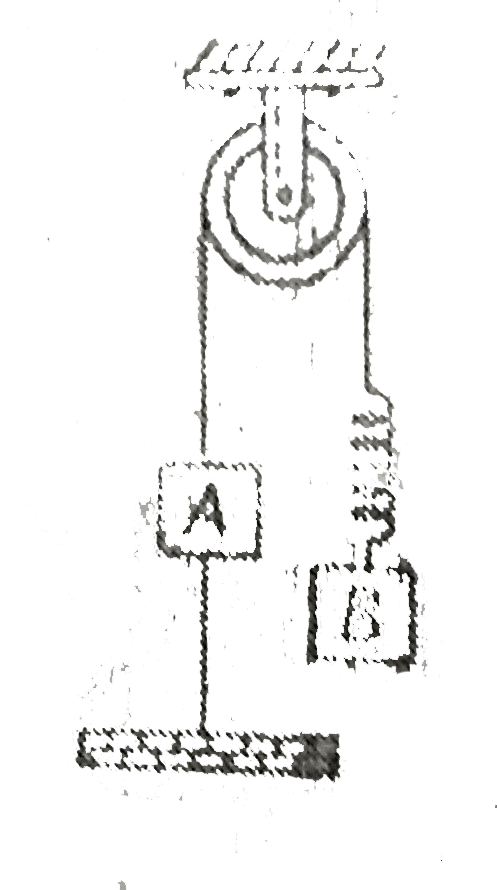
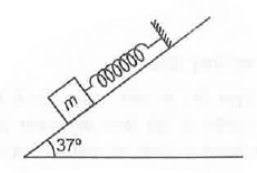
View SolutionIf extension in the spring at equilibrium position is 6 cm then acceleration of block if it is released by further stretching 4 cm.
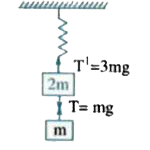
View SolutionThe system shown in the figure is in equilibrium at rest. The spring and string are massless Now the string is cut. Find the acceleration of the blocks just after the string is cut.
View SolutionThe system is released from rest with both the springs in unstretched positions. Mass of each block is 1 kg and force constant of each spring is 10N/m.
In the equilibrium position, speed of the block placed horizontally is
View SolutionTwo springs are in a series combination and are attached to a block of mass 'm' which is in equilibrium. The spring constants and extension in the springs are as shown in the figure. Then the force exerted by the spring on the block is :
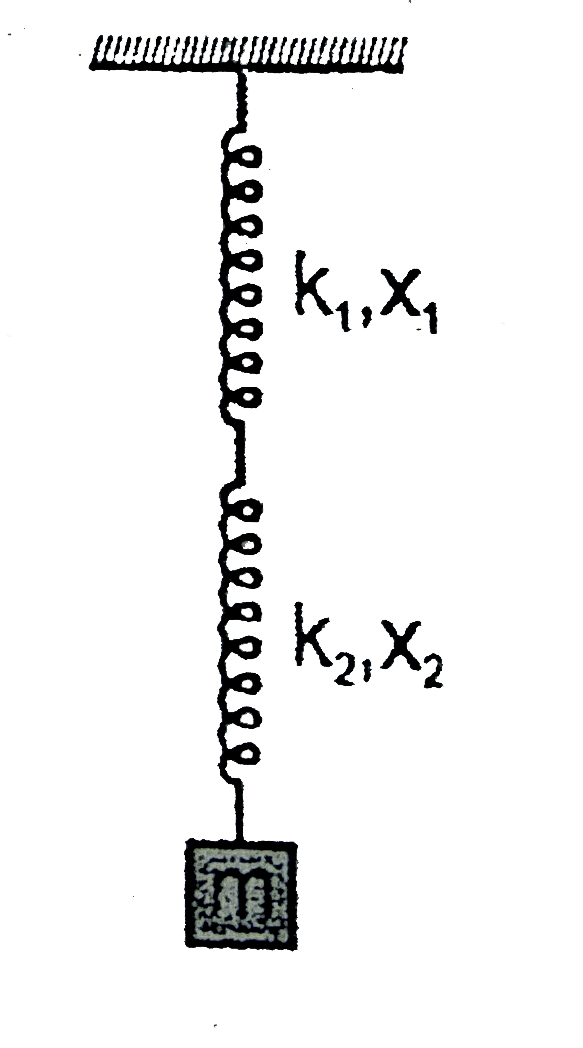
View SolutionA spring mass system oscillates with a frequency v. If it is taken in an elavator slowly accelerating upward, the frequency will
View Solution
