Two bodies A and B of masses m and 2m respectively are placed on a smooth floor. They are connected by a light spring of stiffness k.
A third body C of mass m moves with velocity v0 along the line joining A and B and collides elastically with A. If lo be the natural length of the spring then find the minimum separation between the blocks.

Initially there will be collision between C and A which is elastic, therefore by using conservation of momentum we obtain,
mv0=mvA+mvc, v0=vA+vC
Since e=1,v0=vA−vC
Solving the above two equations, vA=v0 and vc=0.
Now A will move and compress the spring which in turn accelerate B and retard A and finally. both A and B will move with same velocity v.
(a) Since net external force is zero, therefore momentum of the system (A and B) is conserved.
⇒v=v0/3
(b) If x0 is the maximum compression, then using energy conservation
12mv20=12(m+2m)v2+12kx20
⇒12mv20=12(3m)v209+12kx20
⇒x0=v0√2m3k
Hence minimum distance D=l0=x0==l0−v0√2m3k
Similar Questions
Two blocks A and B of masses in and 2m respectively placed on a smooth floor are connected by a spring. A third body C of mass m moves with velocity v0 along the line joining A and B and collides elastically with A. At a certain instant of time after collision it is found that the instantaneous velocities of A and B are same then:

View SolutionTwo blocks A and B of masses m and 2m respectively are placed on a smooth floor. They are connected by a spring. A third block C of mass m moves with a velocity v0 along the line joing A and B and collides elastically with A, as shown in figure. At a certain instant of time t0 after collision, it is found that the instantaneous velocities of A and B are the same. Further, at this instant the compression of the spring is found to be x0. Determine (i) the common velocity of A and B at time t0, and (ii) the spring constant.
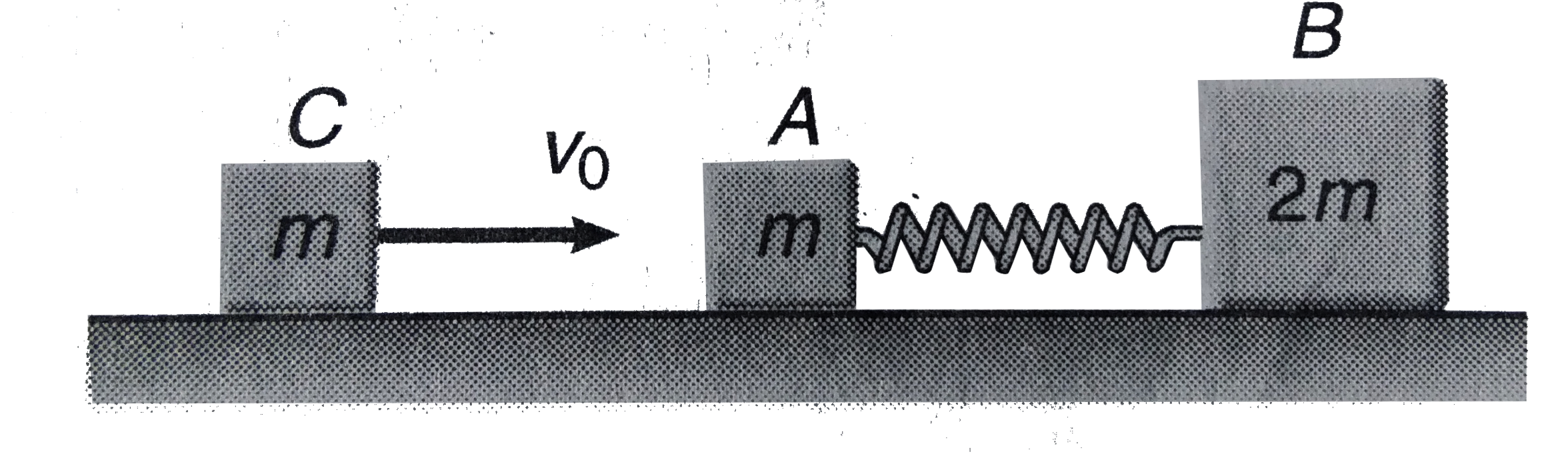
View SolutionTwo blocks A and B. each of mass m, are connected by a massless spring of natural length I. and spring constant K. The blocks are initially resting in a smooth horizontal floor with the spring at its natural length, as shown in Fig. A third identical block C, also of mass m, moves on the floor with a speed v along the line joining A and B. and collides elastically with A. Then

View SolutionTwo blocks A and B of mass m and 2m respectively are connected by a light spring of force constant k. They are placed on a smooth horizontal surface. Spring is stretched by a length x and then released. Find the relative velocity of the blocks when the spring comes to its natural length

View SolutionTwo blocks A and B of mass 2m and m respectively are connected to a massless spring of force constant K as shown in figure A and B are moving on the horizontal frcitionless surface with velocity v to right with underformed spring. If B collides with C elastically, then maximum compression of the spring will be
View SolutionA body of mass m2 moving with velocity v0 collides elastically with another mass of m3 . Find % change in KE of first body
View Solution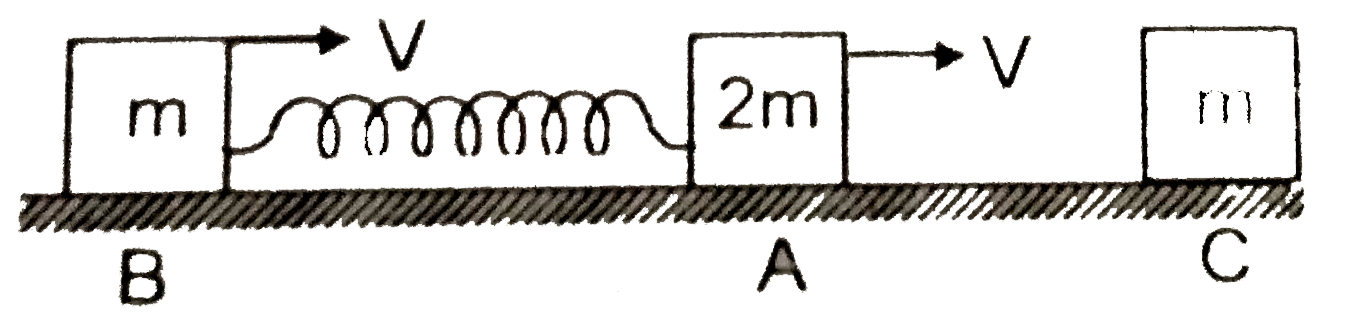
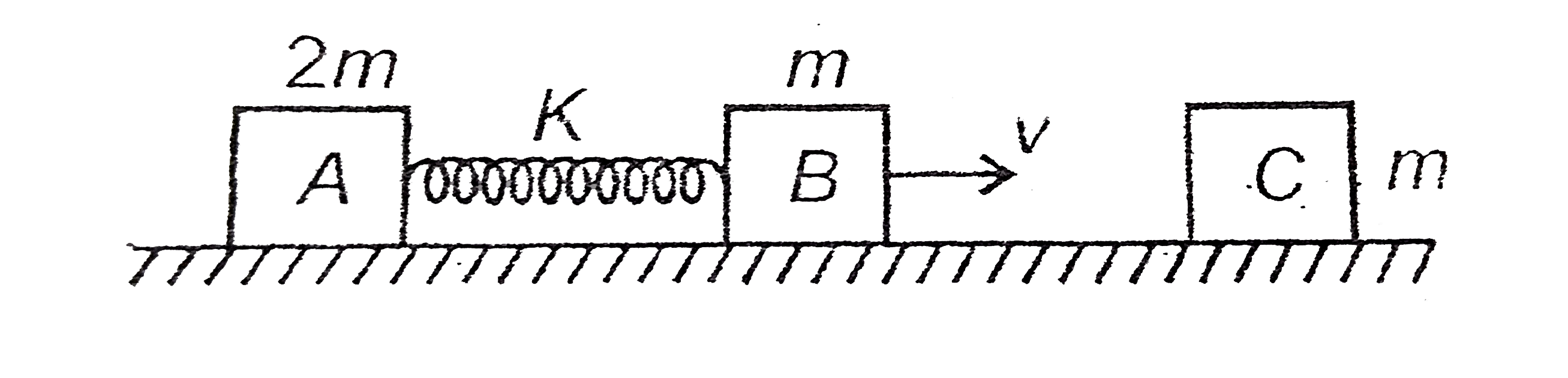
Two blocks A and B of mass 2 m and m respectively are connected to a massless spring of spring constant K. if A and B moving on the horizontal frictionless surface with velocity v to right. If A collides with C of mass m elastically and head on, then the maximum compressions of the spring will be
View SolutionA body of mass m moving with velocity uˆi collides elastically with a body at rest of mass 3m and then the final velocity of body mass m is v ˆj. Find the relation between v and u
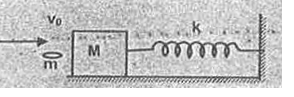
View SolutionA bullet of mass m strikes a block of mass M connected to a light spring of stiffness k, with a speed v0 and gets into it. Find the loss of K.E. of the bullet.
View SolutionTwo blocks A and B of masses in and 2m, respectively, are connected with the help of a spring having spring constant, k as shown in Fig. Initially, both the blocks arc moving with same velocity v on a smooth horizontal plane with the spring in its natural length. During their course of motion, block B makes an inelastic collision with block C of mass m which is initially at rest. The coefficient of restitution for the collision is 1/2. The maximum compression in the spring is
View Solution
