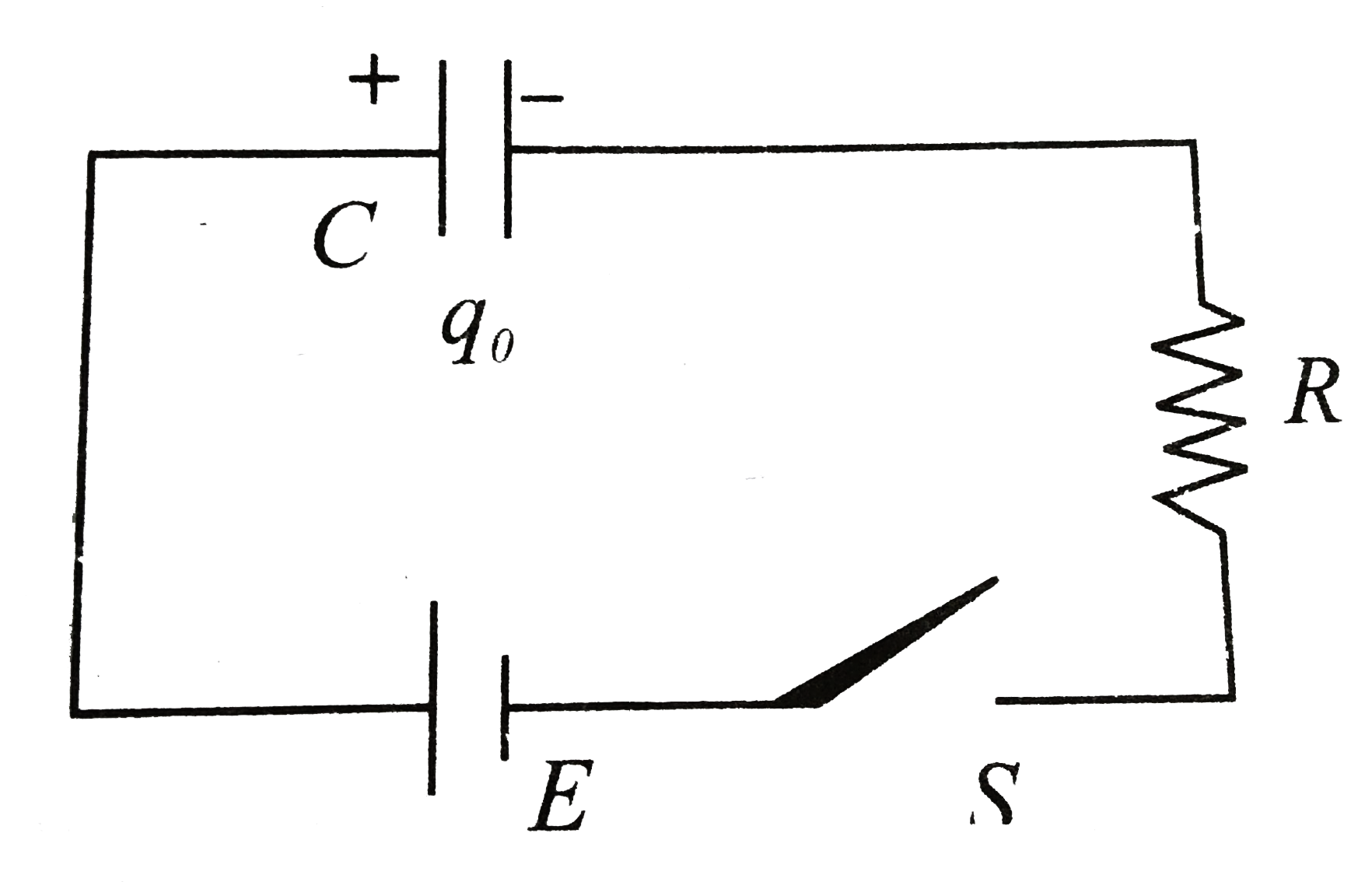
A capacitor C(=100μF) is charged with a total charge of 1.2×10−3C and connected in a circuit as shown. Find the current in the circuit after the key k is closed ( t= 0) as a function of time (t). Notice that the positively charged plate of the capacitor is connected to the negative terminal of the cell

Let the current in the circuit be i(t), and the charge on the capacitor be q(t). Note that the initial polarity of charge q0 on the capacitor is opposite to the final steady state charge. Applying Kirchoff.s laws
qC+R(dqdt)=E,
E=12V,R=10×103ΩC=100×10−6F
or,(dqdt)+qRC=ER
Solving this, q=C1C1e−t/RC+CE where is an arbitrary constant We determine C, from the initial condition, where q0=1.2×10−3C
q=−q0att=0,−q0=C1+CE
Thus, q(t)=−(CE+qo)e−1/RC+CE
The currenti=dqdt=(CE+q0RC)e−1/RC
Substituting, the values, i=(2.4mA)e−t/(sec)
Similar Questions
A capacitor having initial charge q0=CE/2 is connected to a cell of emf E through a resistor R as shown. Find the total heat generated in the circuit after the switch S is closed.
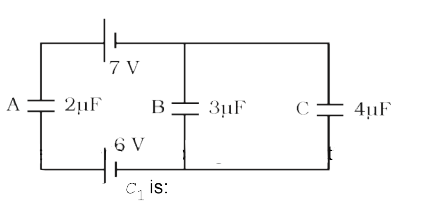
View SolutionThree capacitor A,B, and C, are connected in a circuit as shown in. What is the charge in μC on the capacitor B?
 .
.
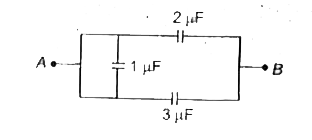
View SolutionIn the given circuit the charge on the plates of 1 μF capacitor, when 100 V battery is connected to the terminals A and B will be
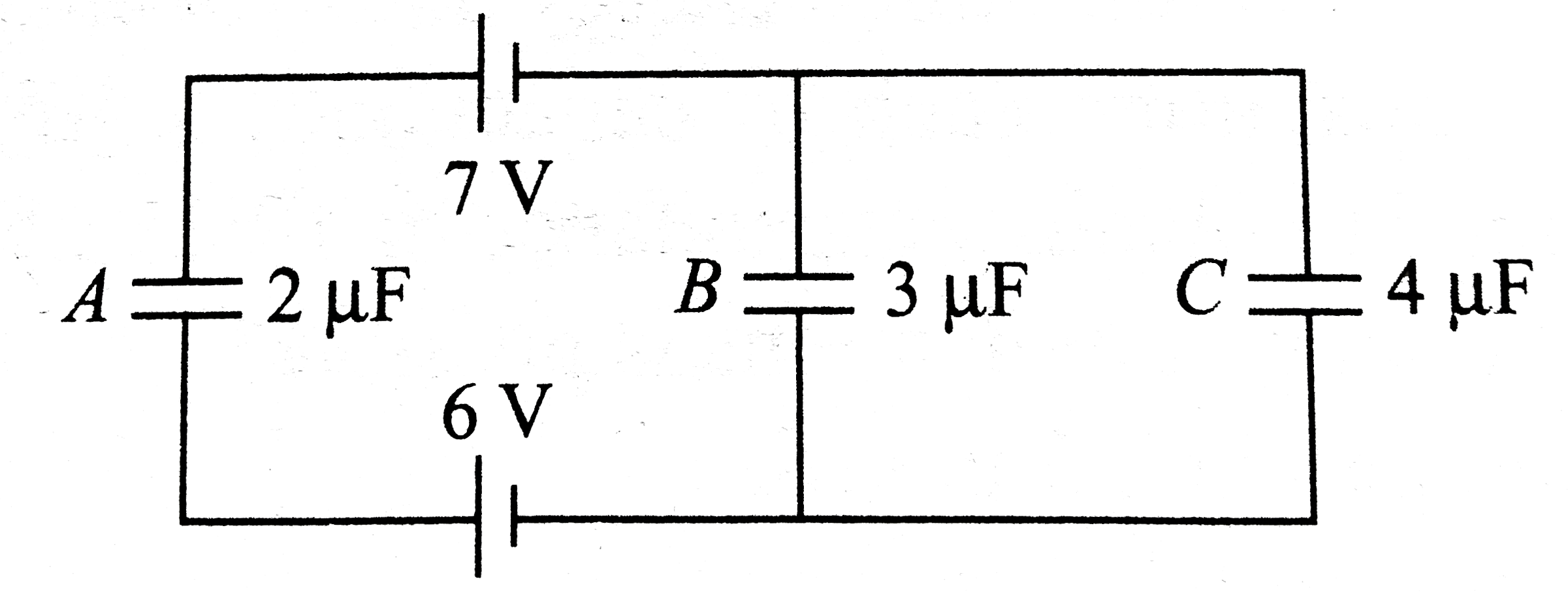
View SolutionThree capacitors A,B and C are connected in a circuit as shown in figure. What is the charge in μC on the capacitor B?
View SolutionIn the circuit shown the key (K) is closed at t=0, the current through the key at the instant t=10−3ln,2 is

View SolutionA capacitor of capacitance C is charged to a potential difference V0 and then connected with a resistance and a battery of EMF 3V0 such that the positively charged plate of the capacitor is connected to the positive terminal of the battery. The total heat generated in the resistance until the current in the circuit becomes zero is n(CV20). the value of n is ________.
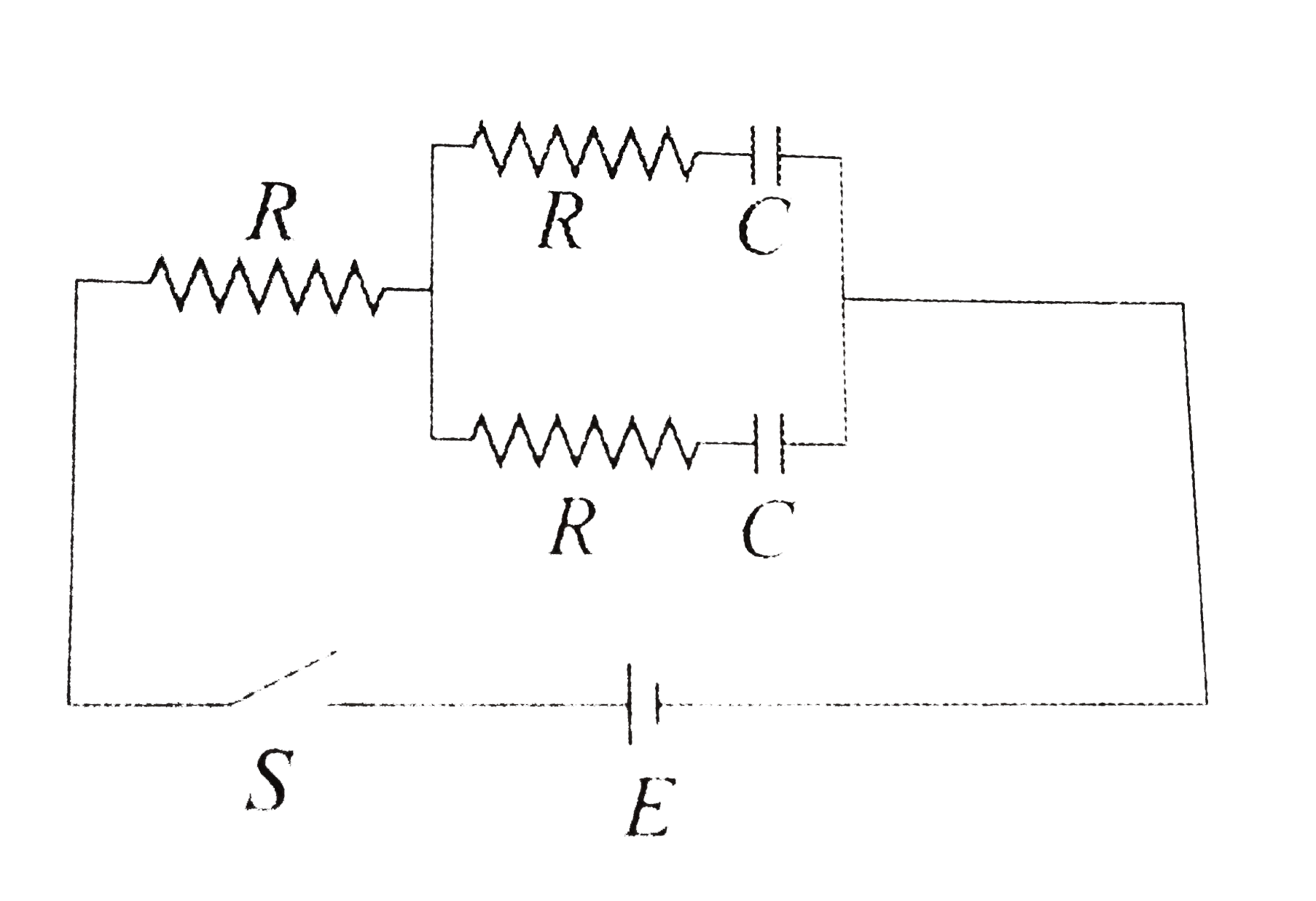
View SolutionThe switch S in the circuit diagram is closed at t = 0. The charge on capacitors at any time is
View SolutionA capacitor is connected to a variable source of potential. Current flowing in the circuit and potential across the plates of capacitor at time t are shown in figure.

Capacity of the capacitor is
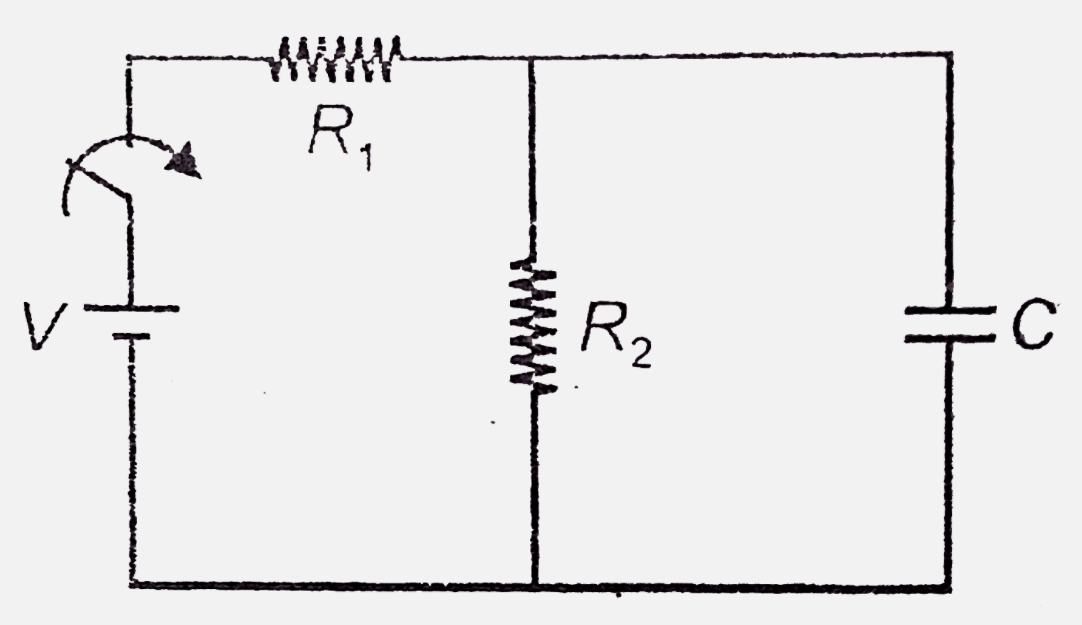
View SolutionConsider the circuit shown. Switch is closed at t=0. Find the current through the battery as a function of time. Initially capacitor was uncharged.
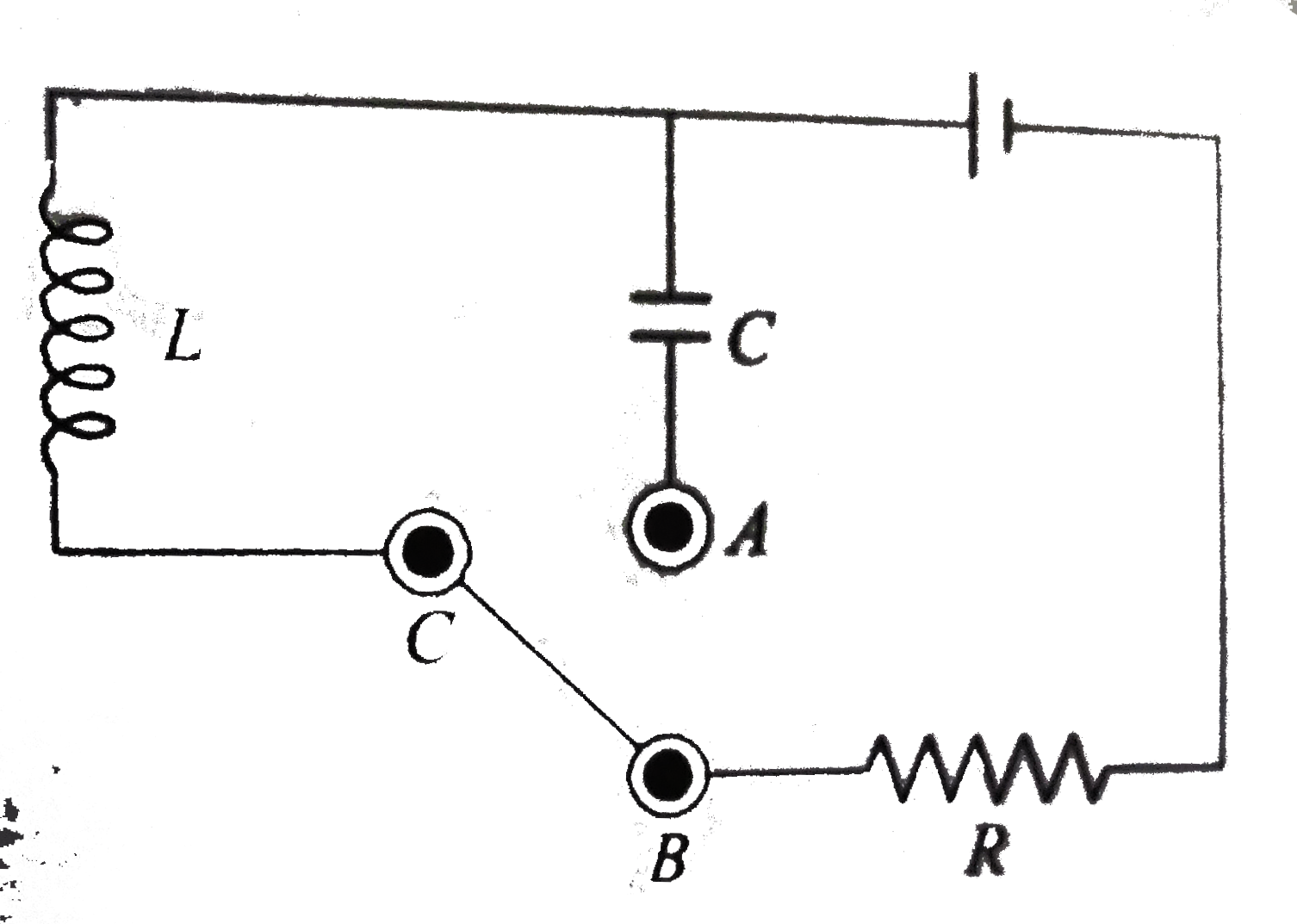
View SolutionIn the circuit shows in Fig the capacitor is initially uncharged and the two - way switch is connected in the position BC. Find the current through the resistence R as a function of time t. After time t=4 ms, the switch is connected in the position AC. Find the frequency of oscillation of the capacitor of the circuit in the position, and the maximum charge on the capacitor C. At what time will the energy stored in the capacitor be one-half of the total energy stored in the circuit? It is given L=2×10−4H,C=5mF,R=In210Ω and emf of the battery =1V.
View Solution
