A capacitor of capacity 1μF is connected in a closed series circuit with a resistance or 107 ohms, an open key and a cell of 2 V with negligible internal resistance :
(i) When the key is switched on at time t=0, find,
(a) The time constant for the circuit.
(b) The charge on the capacitor at steady state.
(c) Time taken to deposit charge equal to half of charge that will deposit at steady state.
(ii) If after completely charging the capacitor, the cell is shorted by zero resistance at time t=0, find the charge on the capacitor at t=50 s. (Given : e−5=6.73×10−3,ln2=0.693)
The correct Answer is:(i)(a)10s(b)2μC (c)10In2=6.93sec.
(ii)q=(2e−5)μC=1.348×10−8C
Step by step video, text & image solution for A capacitor of capacity 1muF is connected in a closed series circuit with a resistance or 10^(7) ohms, an open key and a cell of 2 V with negligible internal resistance : (i) When the key is switched on at time t=0, find, (a) The time constant for the circuit. (b) The charge on the capacitor at steady state. (c) Time taken to deposit charge equal to half of charge that will deposit at steady state. (ii) If after completely charging the capacitor, the cell is shorted by zero resistance at time t=0, find the charge on the capacitor at t=50 s. (Given : e^(-5)=6.73xx10^(-3), ln^(2)=0.693) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CAPACITANCEBOOK - RESONANCECHAPTER - CAPACITANCEEXERCISE - Exercise - 2
74 Videos
- CAPACITANCEBOOK - RESONANCECHAPTER - CAPACITANCEEXERCISE - Exercise - 3
26 Videos
- CAPACITANCEBOOK - RESONANCECHAPTER - CAPACITANCEEXERCISE - Miscellaneous Solved Example
3 Videos
- ATOMIC PHYSICSBOOK - RESONANCECHAPTER - ATOMIC PHYSICSEXERCISE - Advanved level problems
17 Videos
- COMMUNICATION SYSTEMSBOOK - RESONANCECHAPTER - COMMUNICATION SYSTEMSEXERCISE - Exercise 3
13 Videos
Similar Questions
A coil of inductance 2H and resistance 10Ω are in a series circuit with an open key and a cell of constant 100V with negligible resistance. At time i=0, the key is closed. Find
(a) the time constant of the circuit.
(b) the maximum steady current in the circuit.
(c) the current in the circuit at f=1s.
View SolutionIn the circuit shown all the resistors are of same resistance R=11Ω and C=2μF. They are connected through a battery of 10 V. When the cell is switched on, find
(a) maximum current in the circuit, and
(b) energy stored in the capacitor after time t
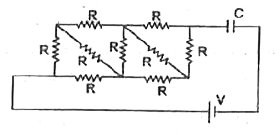
View Solution
Knowledge Check
In given circuit, switch S is closed at t=0 . The charge on the capacitor ar steady state will be
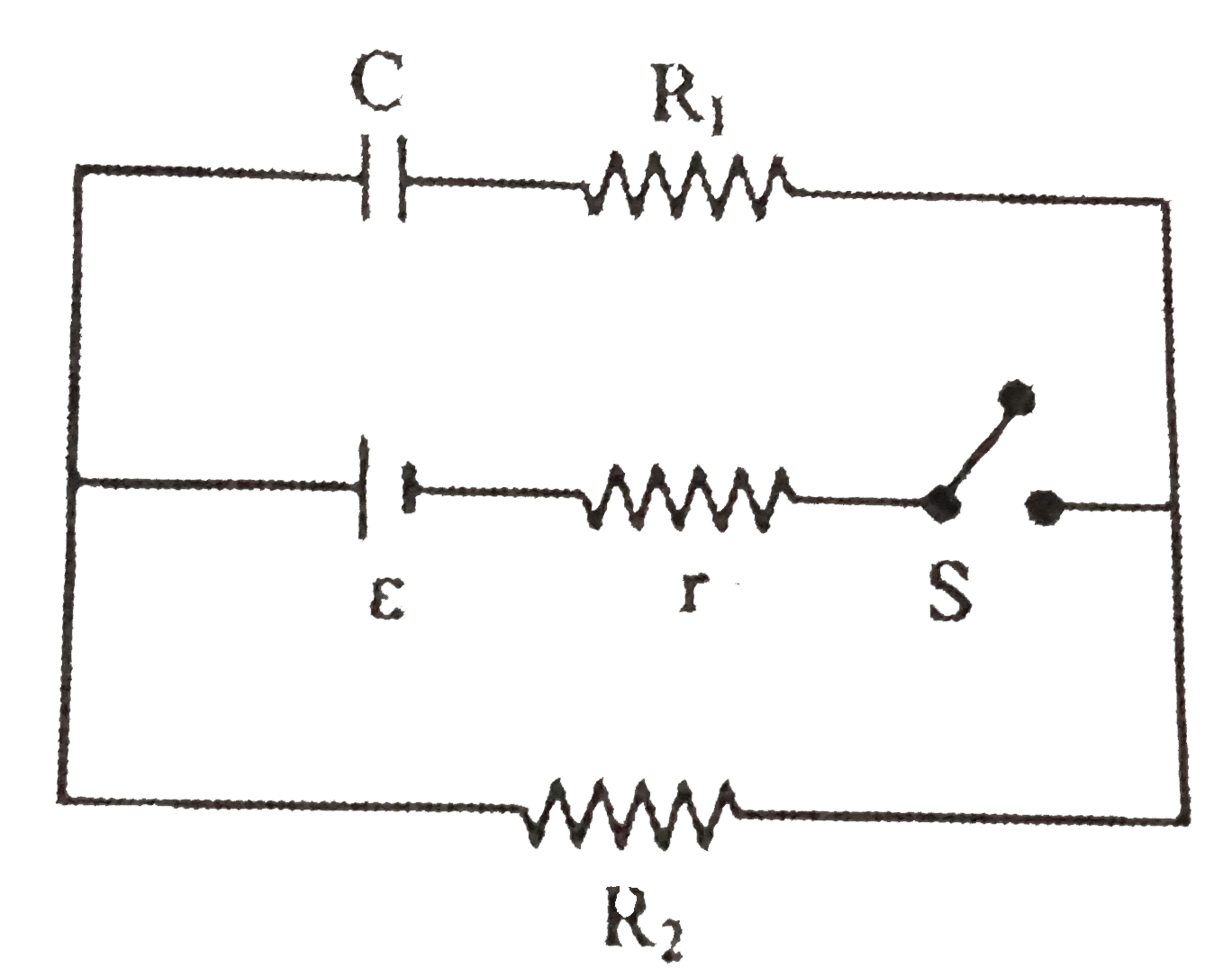ACεR1r+R1BCεR2r+R2CCεR2r+R1DCεR1r+R2The switch S in the circuit diagram is closed at t = 0. The charge on capacitors at any time is
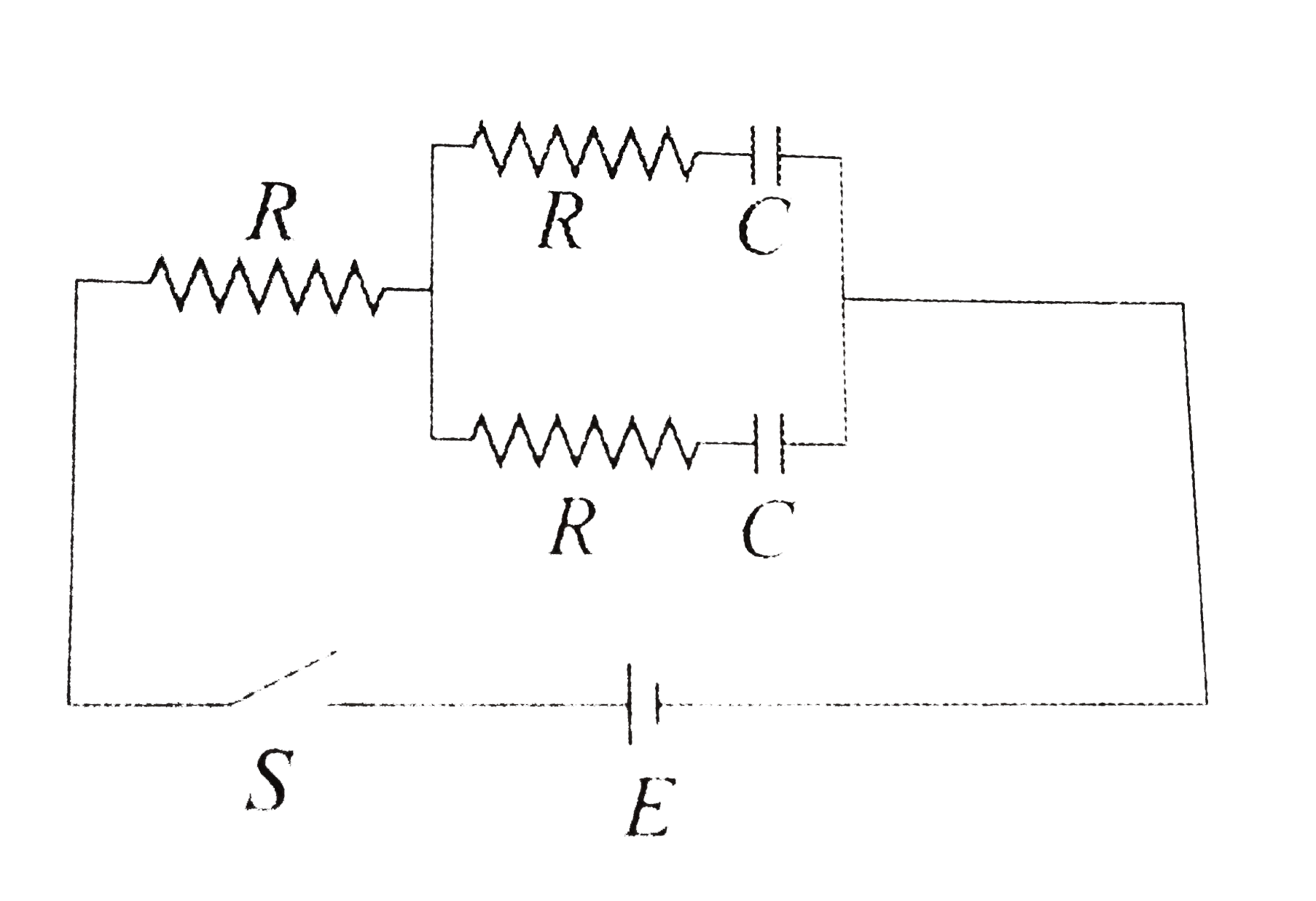Aqt=EC(1−e−2t/3RC)Bqt=EC(1−e−t/2RC)Cqt=EC(1−e−t/3RC)Dqt=EC(1−e−3t/2RC)The charge on a capacitor decrease η time in time t, when it discharging through a circuit with a time constantτ
At=ητBt=τ1nηCt=τ(1nη−1)Dt=τ1n(1−1η)
A capacitor of capacitance 100(μ)F is charged by connecting it to a battery of emf 12 V and internal resistance 2(Ω). (a) Find the time constant of the circuit. (b) Find the time taken before 99% of maximum charge is stored on the capacitor.
View SolutionThe circuit is in a steady state.
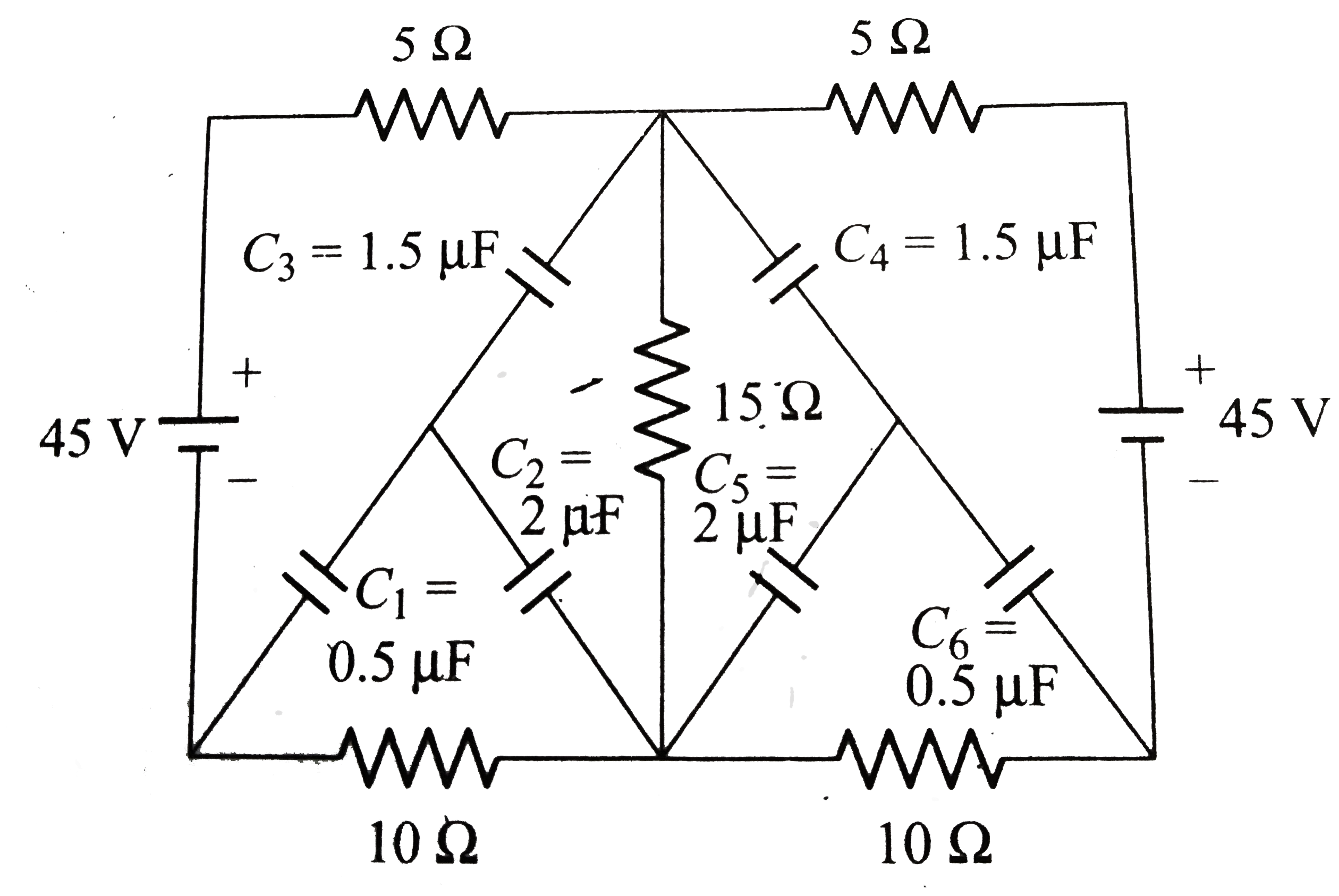
The charge in capacitor C1 is
View SolutionThe circuit is in a steady state.
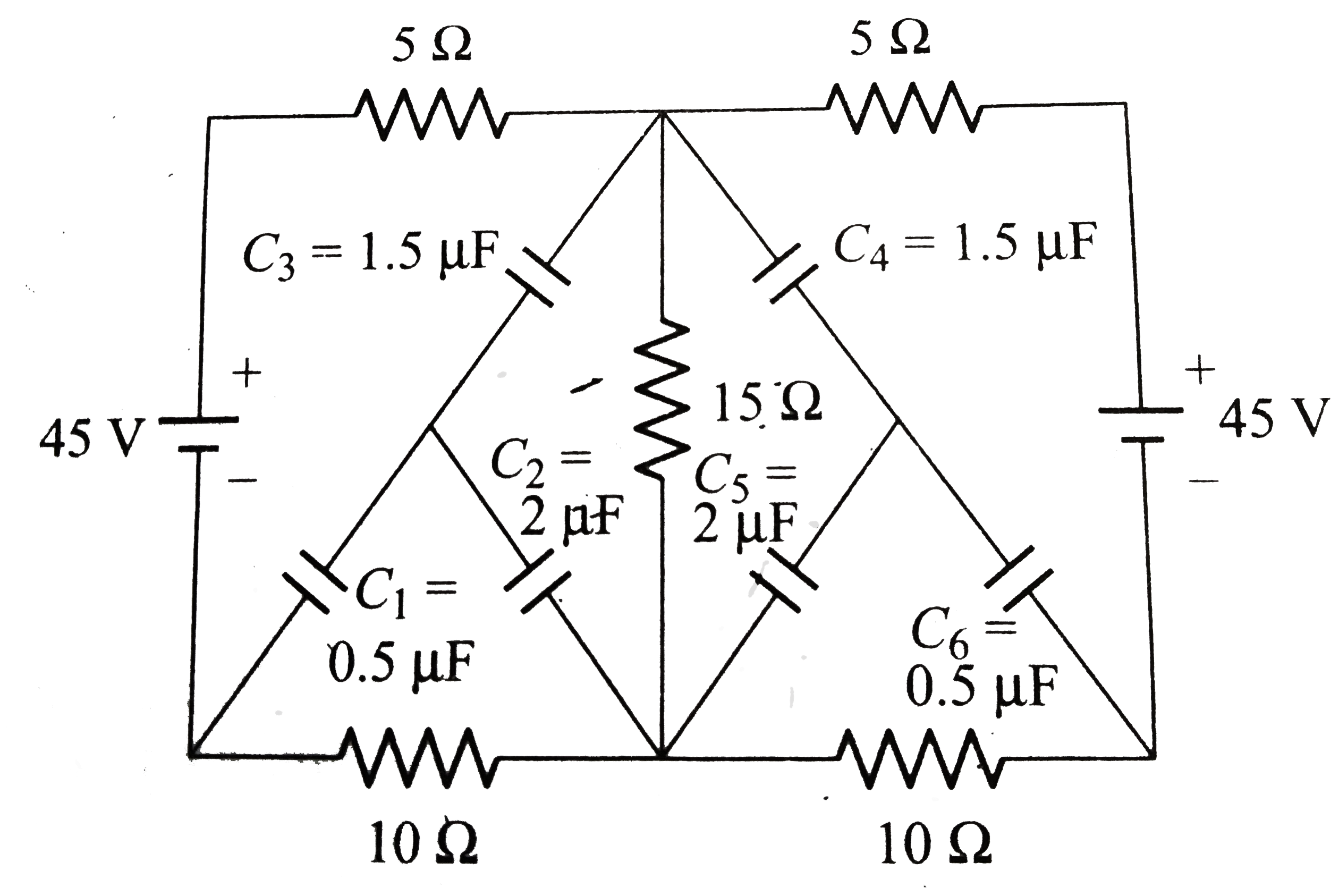
The charge in capacitor C2 is
View SolutionA capacitor with capacitance C is charged to Q0 and then connected in the circuit shown. When key is closed, what is charge on this capacitor in steady state?
View SolutionA capacitor of capacitance C is connected in series with a resistance R and a DC source of emf E through a key. The capacitor starts charging when the key is closed. By the time the capacitor has been fully charged, what amount of energy is dissipated in the resistance R?
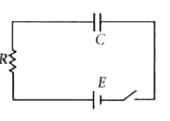
View Solution