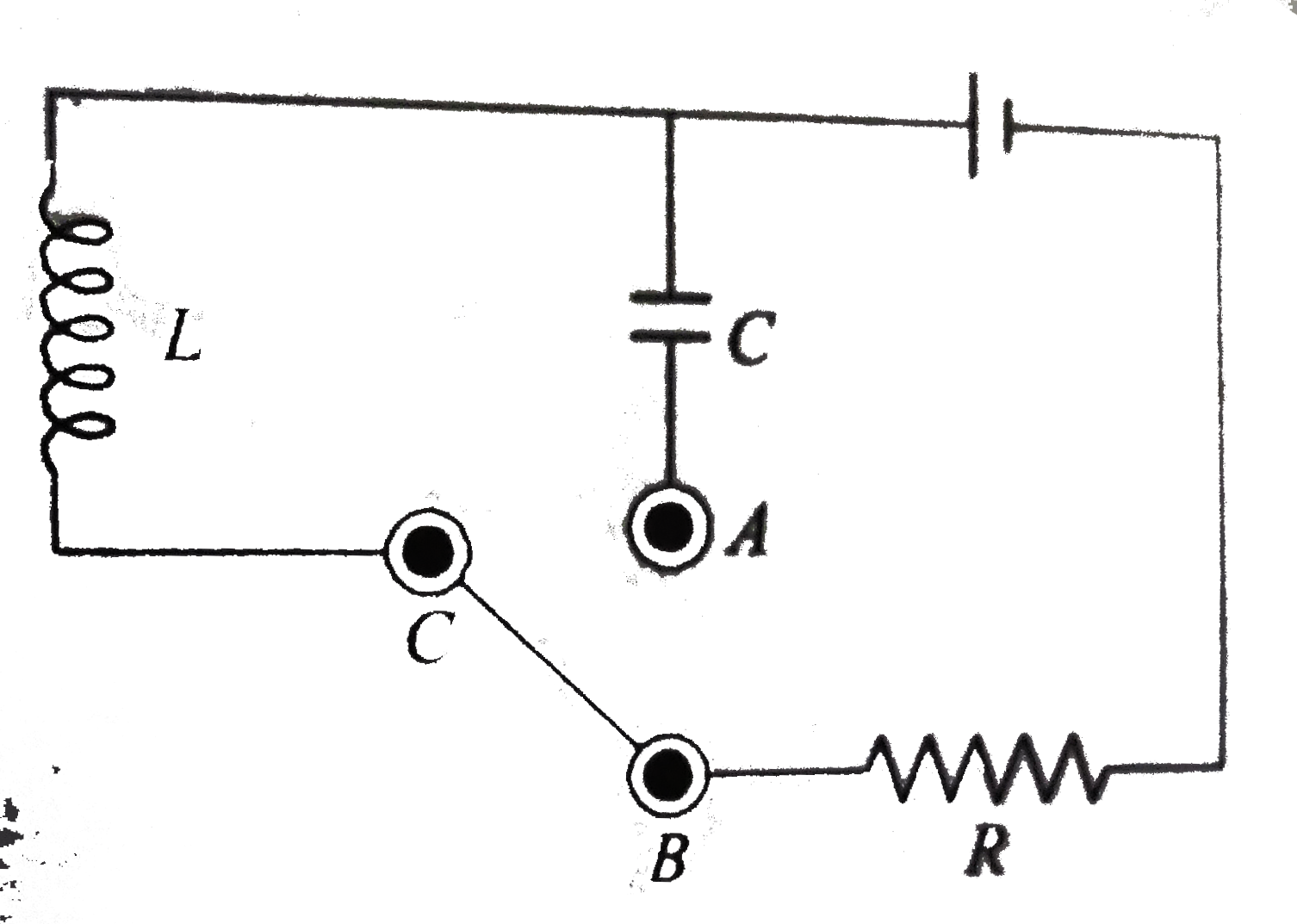
In the circuit shows in Fig the capacitor is initially uncharged and the two - way switch is connected in the position BC. Find the current through the resistence R as a function of time t. After time t=4 ms, the switch is connected in the position AC. Find the frequency of oscillation of the capacitor of the circuit in the position, and the maximum charge on the capacitor C. At what time will the energy stored in the capacitor be one-half of the total energy stored in the circuit? It is given L=2×10−4H,C=5mF,R=In210Ω and emf of the battery =1V.
The correct Answer is:10In2⎛⎝1−(12)t2×10−3⎞⎠;103rads−1;7.5×10−3In2C;
4ms+nπ+(−1)nπ/4ω
Current in R or L at any time is given by:
I=ɛR(1−e−Rt/L)⇒I=1(In2)/10[1−e−tIn210×2×10−4]
⇒I=10In2⎡⎣1−eIn2−(t2×10−3)⎤⎦⇒I=10In2⎡⎣1−(12)t2×10−3⎤⎦
Now at t=4ms
I=10In2⎡⎢⎣1−(12)4×10−32×10−3⎤⎥⎦=10In2[1−14]=152In2A
Now the switch is shifted between A and C. Just after shifting the switch, current in inductor will be as calculated above. It can't change at once. Now due to this current, the capacitor will start charging. Frequency of oscillation is given by :
ω=1√LC=1√2×10−4×5×10−3=103rad/s
To find maximum charge : Q22C=12LI2
⇒Q=(√LC)I=10−3×152In2⇒Q=7.5×10−3In2C
Energy in the capacitor is half of total energy when charge on
capacitor is q=Q√2
Charge on capacitor at any time
q=Qsinωt[∵att=0,q=0]
⇒Q√2=Qsinωt⇒ωt=nπ+(−1)nπ4
(1) ⇒t=nπ+(−1)nπ/4ω
Total time, T=4ms+nπ+(−1)nπ/4ω
Related Playlists
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Exercises (single Correct )65videos
INDUCTANCE
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Exercises (multiple Correct )7videos
INDUCTANCE
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Exercise 4.124videos
INDUCTANCE
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit27videos
HEATING EFFECT OF CURRENT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type2videos
MAGNETIC FIELD AND MAGNETIC FORCES
Similar Questions
In the circuit shown, switch S is closed at time t=0. Find the current through the inductor as a function of time t.
 View Solution
View SolutionIn the circuit shown in figure, the capacitors are initially uncharged. The current through resistor PQ just after closing the switch is
 View Solution
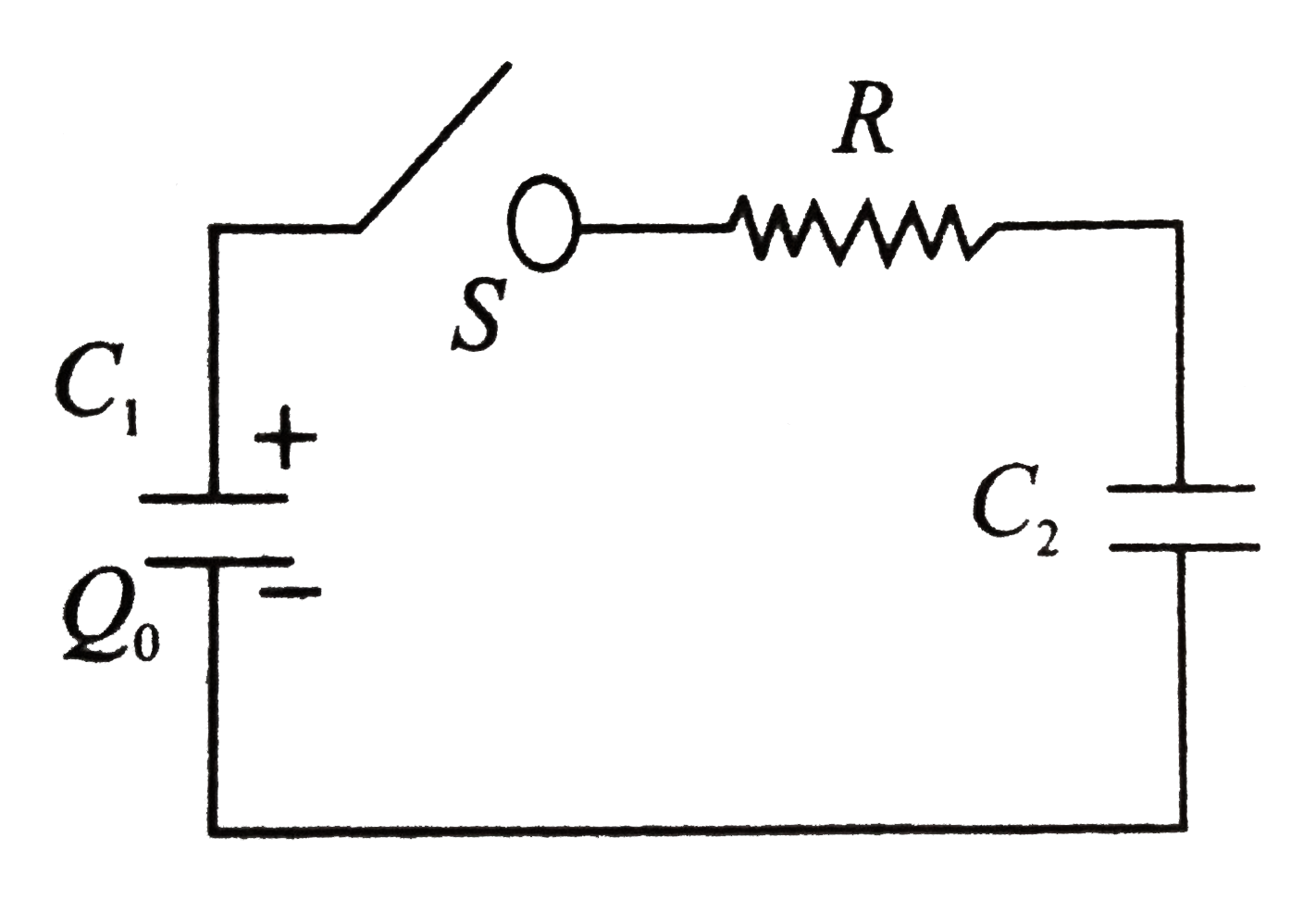
View SolutionIn the circuit shown, the capacitor C1 is initially charged with charge q0. The switch S is closed at time t = 0 . The charge on C2 after time t is
 View Solution
View SolutionIn the circuit in Fig. switch S1 was closed for a long time . At time t=0 the switch is opened.
Find the angular frequency of oscillation of the charge on the capacitor.View Solution
In the circuit shown, all the capacitors are initially uncharged. The current through the battery just after closing the switch 'S' isView SolutionConsider the circuit shown. Switch is closed at t=0. Find the current through the battery as a function of time. Initially capacitor was uncharged.
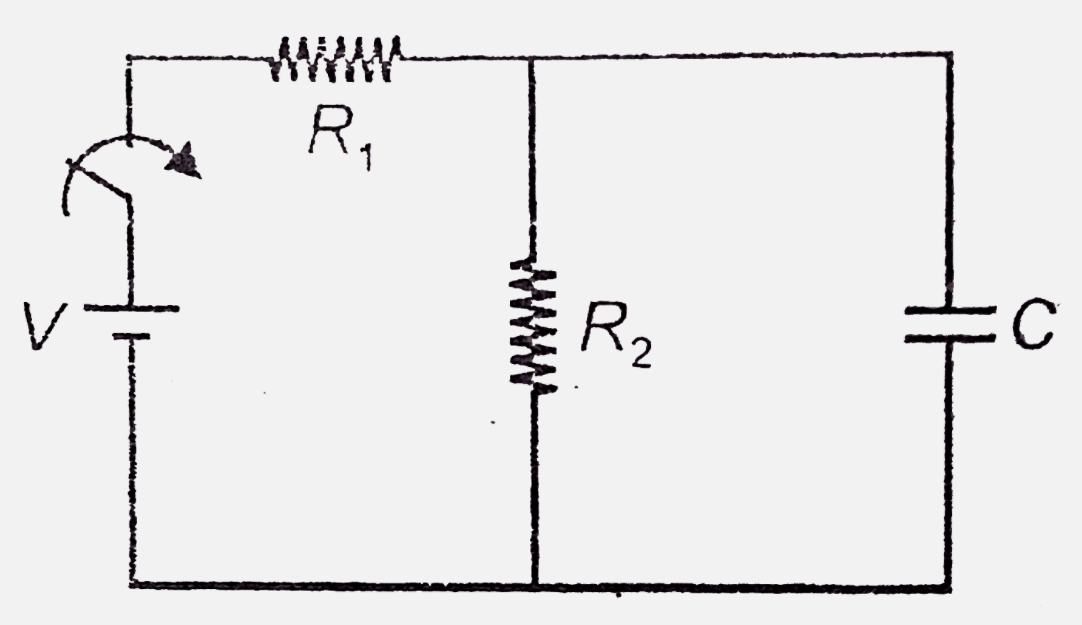 View Solution
View SolutionSwitch S is cloesd in the circuit at time t=0. Find the current through the capacitor and the inductor at any time t
 View Solution
View SolutionIn the circuit shown in fig. when the switch is closed, the capacitor charges with a time constant
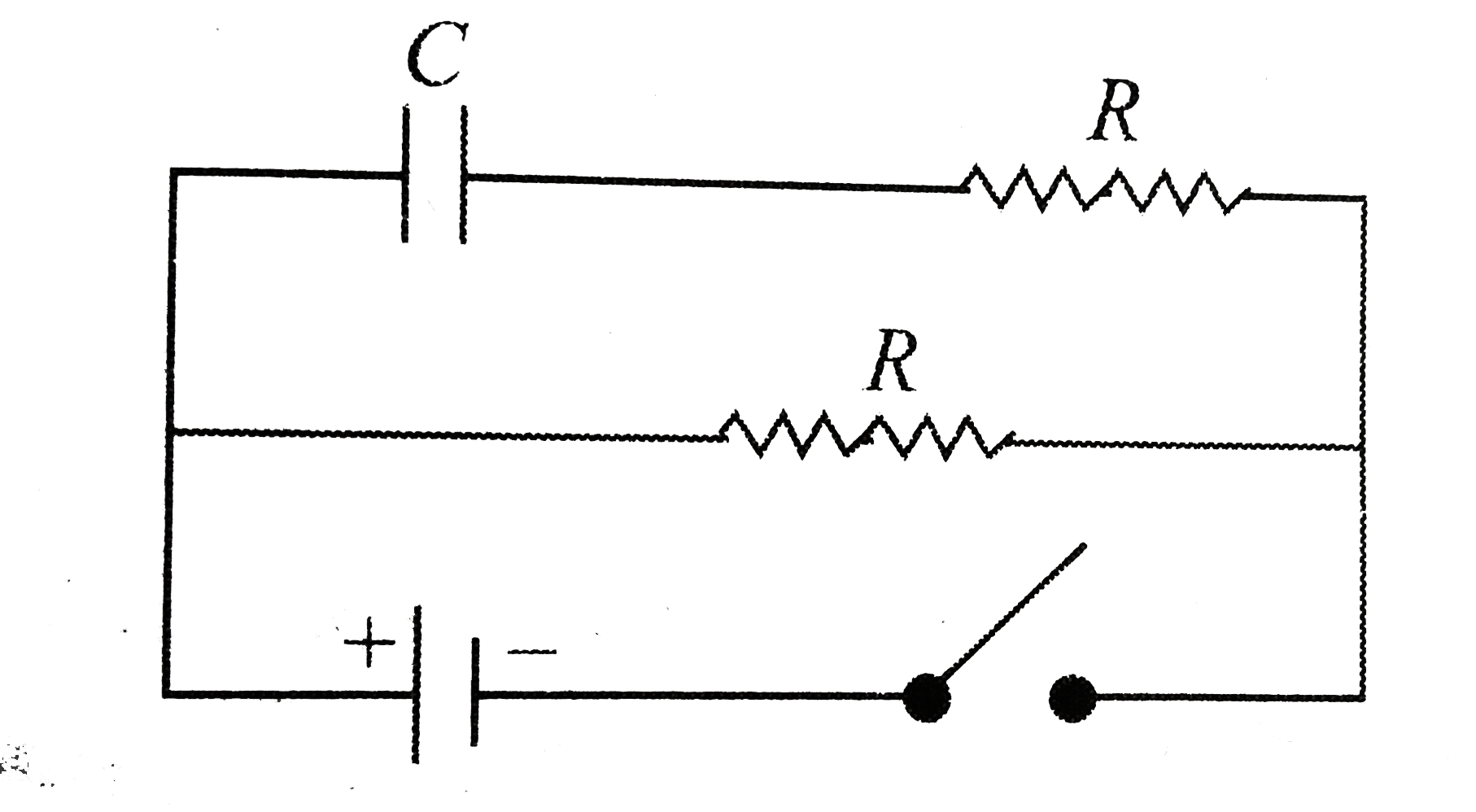 View Solution
View SolutionThe switch in figure is closed at time t=0. Find the current in the inductor and the current through the switch as functions of time thereafter.
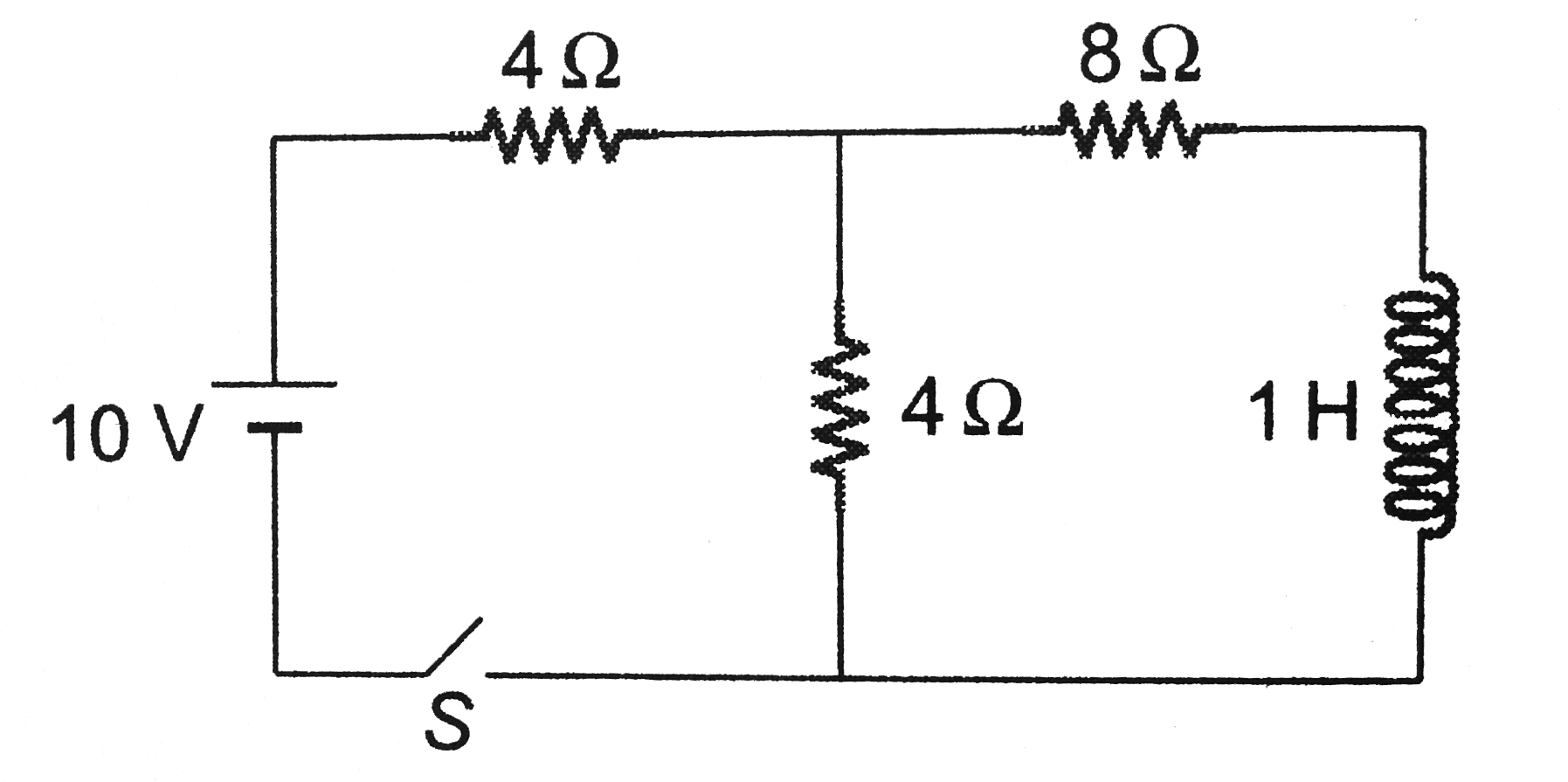 View Solution
View SolutionPassage-III
In the circuit shown, the battery is ideal with emf V. The capacitor is initially uncharged. The switch is closed at time t = 0
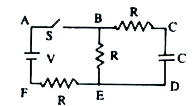
The current in branch containing capacitors at any time t isView Solution


