Two capacitors of capacitances 2C and C are connected in series with an inductor of inductance L. Initially, capacitors have charge such that VB−VA=4V0 and VC−VD=V0. Initial current in the circuit is zero. Find
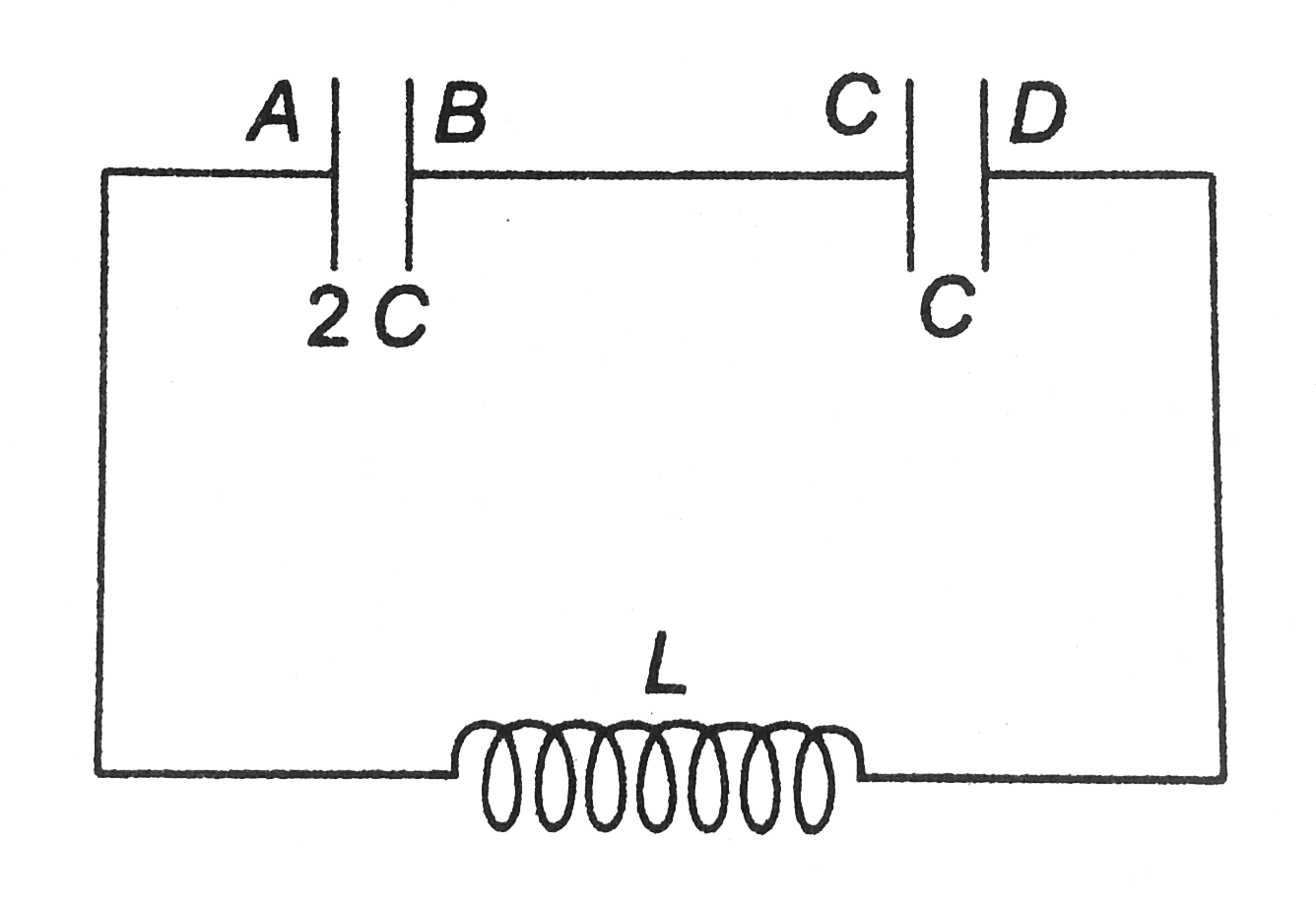
(a) maximum current that will flow in the circuit,
(b) potential difference across each capacitor at that instant,
(c) equation of current flowing towards left in the inductor.
The correct Answer is:I0=V0√6CL; b. V1=3V0,V2=3V0; c. V0√6CLsin√32CLt
a. Applying loop equation in Fig (b)
q'12C−q'2C−LdIdt=0
or LdIdt=(q1−2q22C)−3q2C (i)


Differeentiating (i), we get
Ld2Idt2=−32CI (ii)
Solution of (ii) is I=I0sin(ωt+ϕ)
where ω2=32CL⇒ω=√32CL
but initial current is zero, i.e., at t=0,i=0, putting this above we get I=I0sinωt (iii)
⇒dIdt=I0ωcosωt
putting dI/dt in Eq.(i), LI0ωcosωt=(q1−2q22C)−3q2C (iv)
At t=0,q=0, putting this in the above equation, we get
LI0ω=(q1−2q22C)⇒LI0√32CL=(8CV0−2CV02C)
⇒I0=V0√6CL→ the maximum value of current
b. From (iii) maximum current occurs at ωt=π/2,3π/2, ...etc,
and at these instants from (i) we get q=(q1−2q23)
Potential difference across each capacitor at this instant,
V1=q'12C=12C[q1−(q1−2q23)]
V1=(q1+q2)3C=3V0
V2=q'2C=1C[q2−(q1−2q23)]
V2=(q1+q2)3C=3V0
c. Equation of current:
I=I0sinωt=V0√6CLsin√32CLt
Topper's Solved these Questions
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Exercises (single Correct )
65 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Exercises (multiple Correct )
7 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Exercise 4.1
24 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
27 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type
2 Videos
Similar Questions
Two capacitors of capacitance C and 3C are charged to potential difference V0 and 2V0, respectively, and connected to an inductor of inductance L as shows in Fig. Initially, the current in the inductor is zero. Now, switch S is closed.
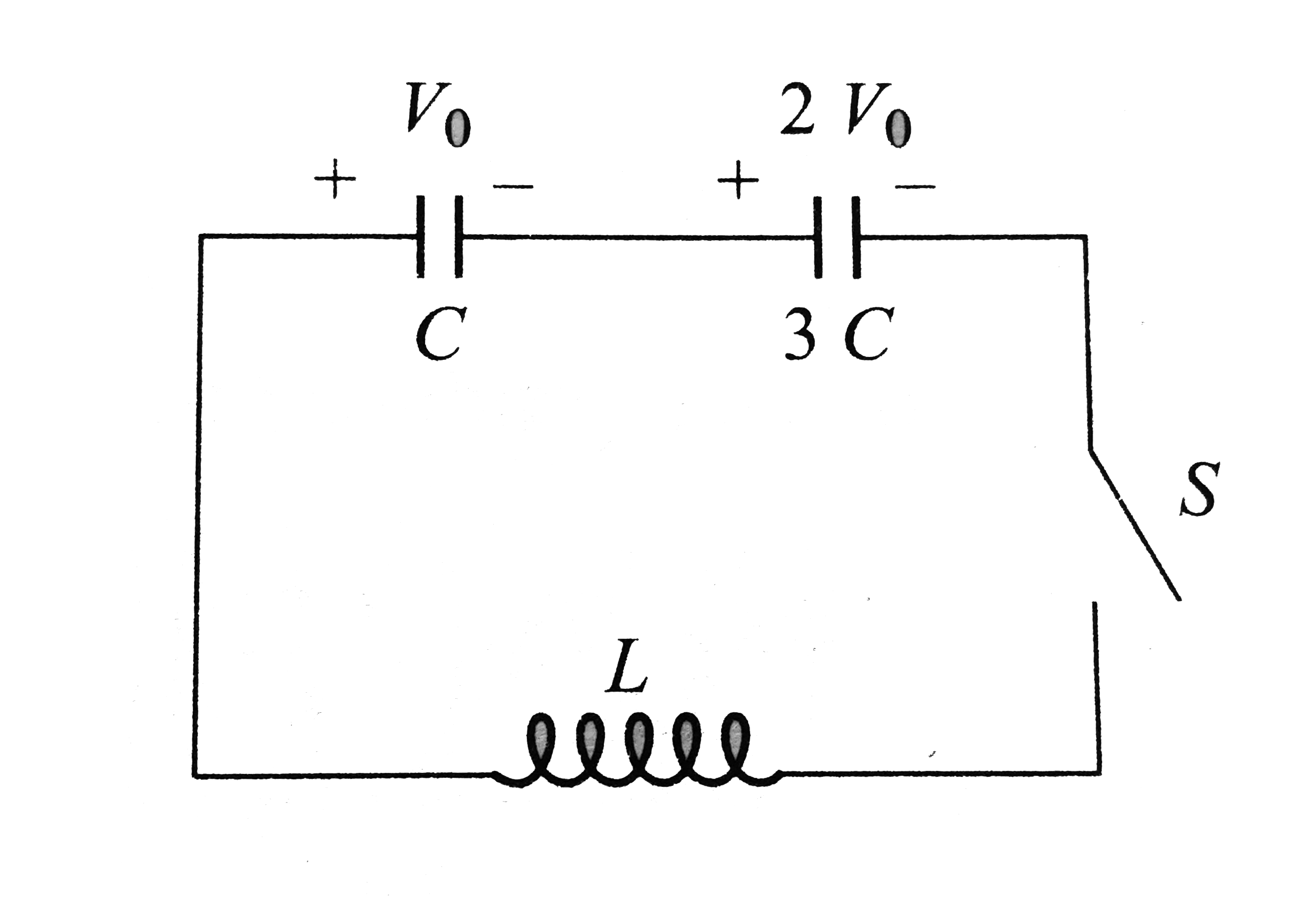
The maximum current in the inductor is
View SolutionTwo capacitors of capacitances 20.0pF and 50.0pF are connected in series with a 6.00V bettery . Find (a )the potential difference across each capacitor and (b) the energy stored in each capacitor .
View SolutionTwo capacitors of capacitance C and 3C are charged to potential difference V0 and 2V0, respectively, and connected to an inductor of inductance L as shows in Fig. Initially, the current in the inductor is zero. Now, switch S is closed.
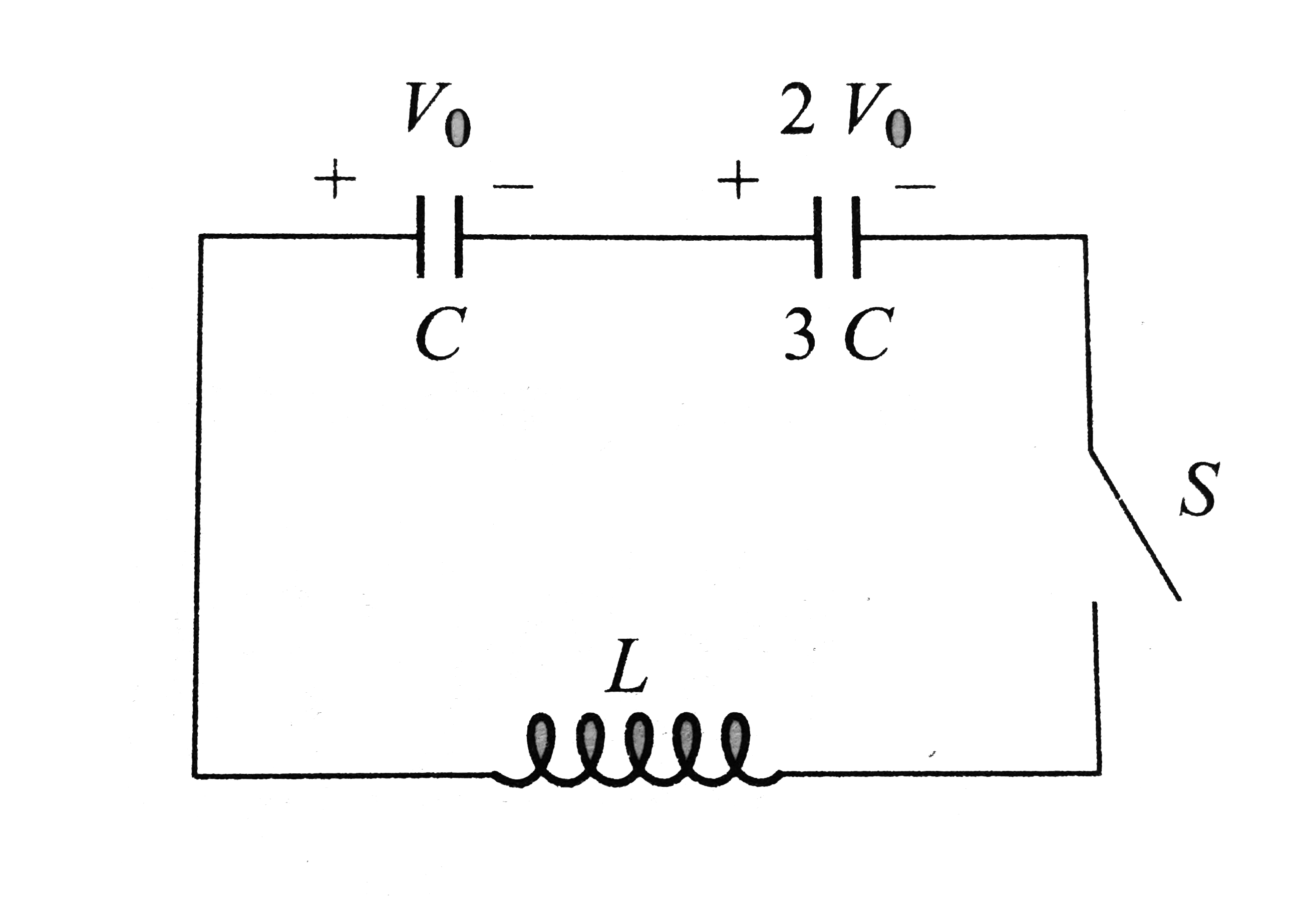
Potential difference across capacitor of capacitance 3C when the current in the circuit is maximum is
View SolutionTwo capacitors of capacitance C and 3C are charged to potential difference V0 and 2V0, respectively, and connected to an inductor of inductance L as shows in Fig. Initially, the current in the inductor is zero. Now, switch S is closed.
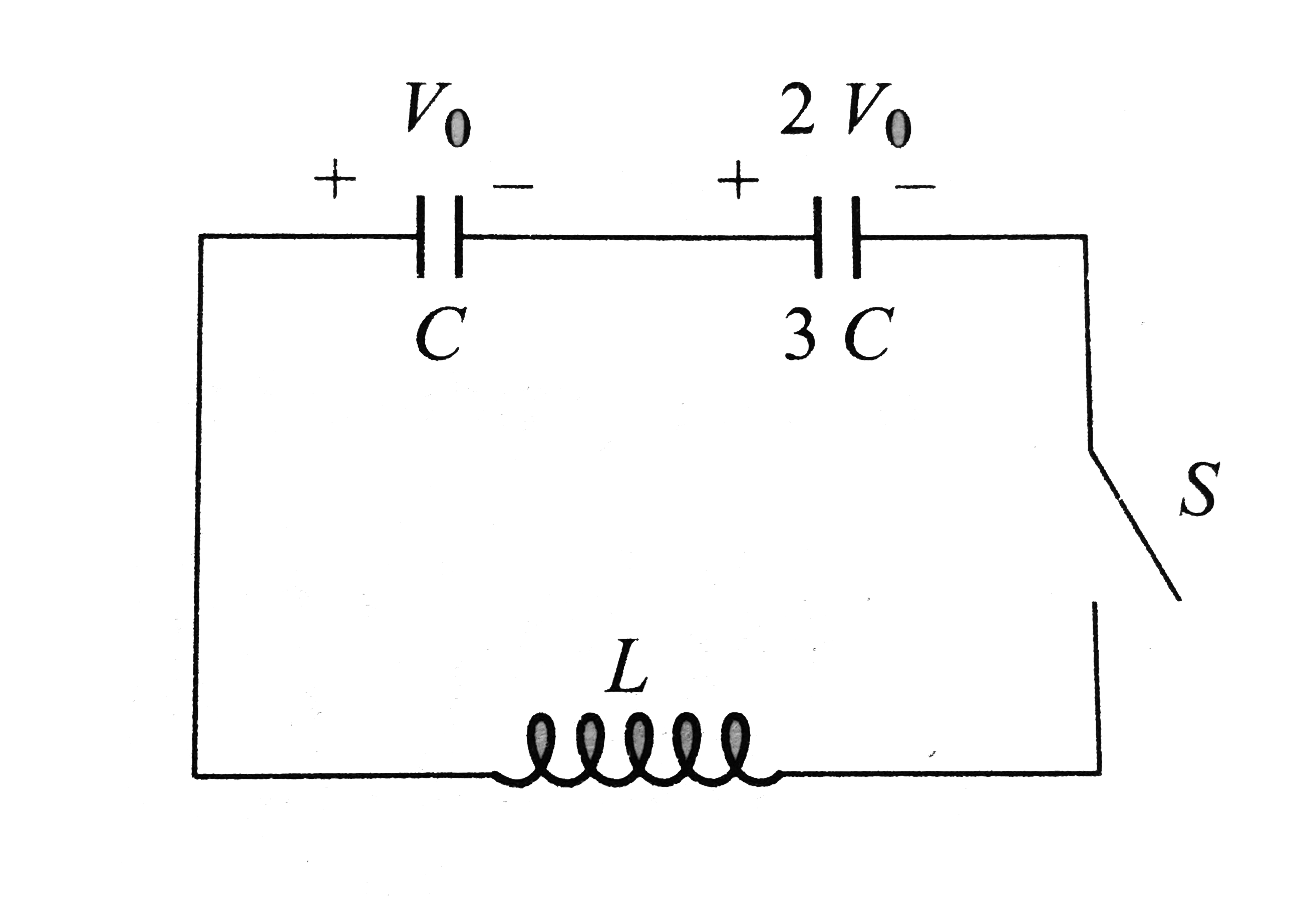
Potential difference across capacitor of capacitance C when the current in the circuit is maximum is
View SolutionTwo capacitors of capacitances C1=2μF and C2=8μF are connected in series and the resulting combination is connected across a 300V battery. Calculate the charge, potential difference and energy stored in the capacitor separately.
View SolutionAn inductor of inductance 20 mH is connected across a charged capacitor of capacitance 5 μF & resulting L-C circuit is set oscillating at its natural frequency . The maximum charge q is 200 μ C on the capacitor . Find the potential difference across the inductor when the charge is 100 μC .
View SolutionA capacitor of capacity 2μF is changed to a potential different of 12V . It is then connected across an inductor of inductance 0.6mH What is the current in the circuit at a time when the potential difference across the capacitor is 6.0V ?
View SolutionA capacitor of capacity 2μF is changed to a potential different of 12V . It is then connected across an inductor of inductance 0.6mH What is the current in the circuit at a time when the potential difference across the capacitor is 6.0V ?
View SolutionTwo capacitor of capacitance 2μFand3μF respectively are charged to potential difference 20 V each. Now the capacitors are connected such that the positively chargd plate of one capacitory is connected to the negatively charged plate of the other. after the current in the circuit has become negligible, the potential difference across the 2μF capacitor is ____V.
View SolutionA capacitor of capacitance 1μF is charged to a potential of 1V, it is connected in parallel to an inductor of inductance 10−3H. The maximum current that will flow in the circuit has the value
View Solution
