Two capacitors of capacitance C and 3C are charged to potential difference V0 and 2V0, respectively, and connected to an inductor of inductance L as shows in Fig. Initially, the current in the inductor is zero. Now, switch S is closed.

Potential difference across capacitor of capacitance C when the current in the circuit is maximum is
V04
3V04
5V04
None of these
The correct Answer is:C
When current is maximum didt=0
∴ e.m.f. across L=0, so potential difference across the capacitor will be same.
From the law of conservation of charge on plates 2 and 3,
3CV+CV=6CV0−CV0
⇒V=5V04
Loss in energy of capacitor = energy stored in inductor
⇒12CV20+123C(2V0)2−12×4CV2=12LI2
⇒I=32V0√3CL


Topper's Solved these Questions
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Exercises (integer)
8 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Archives (fills In The Blanks)
3 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Exercises (assertion-reasoning)
2 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
27 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type
2 Videos
Similar Questions
Two capacitors of capacitance C and 3C are charged to potential difference V0 and 2V0, respectively, and connected to an inductor of inductance L as shows in Fig. Initially, the current in the inductor is zero. Now, switch S is closed.
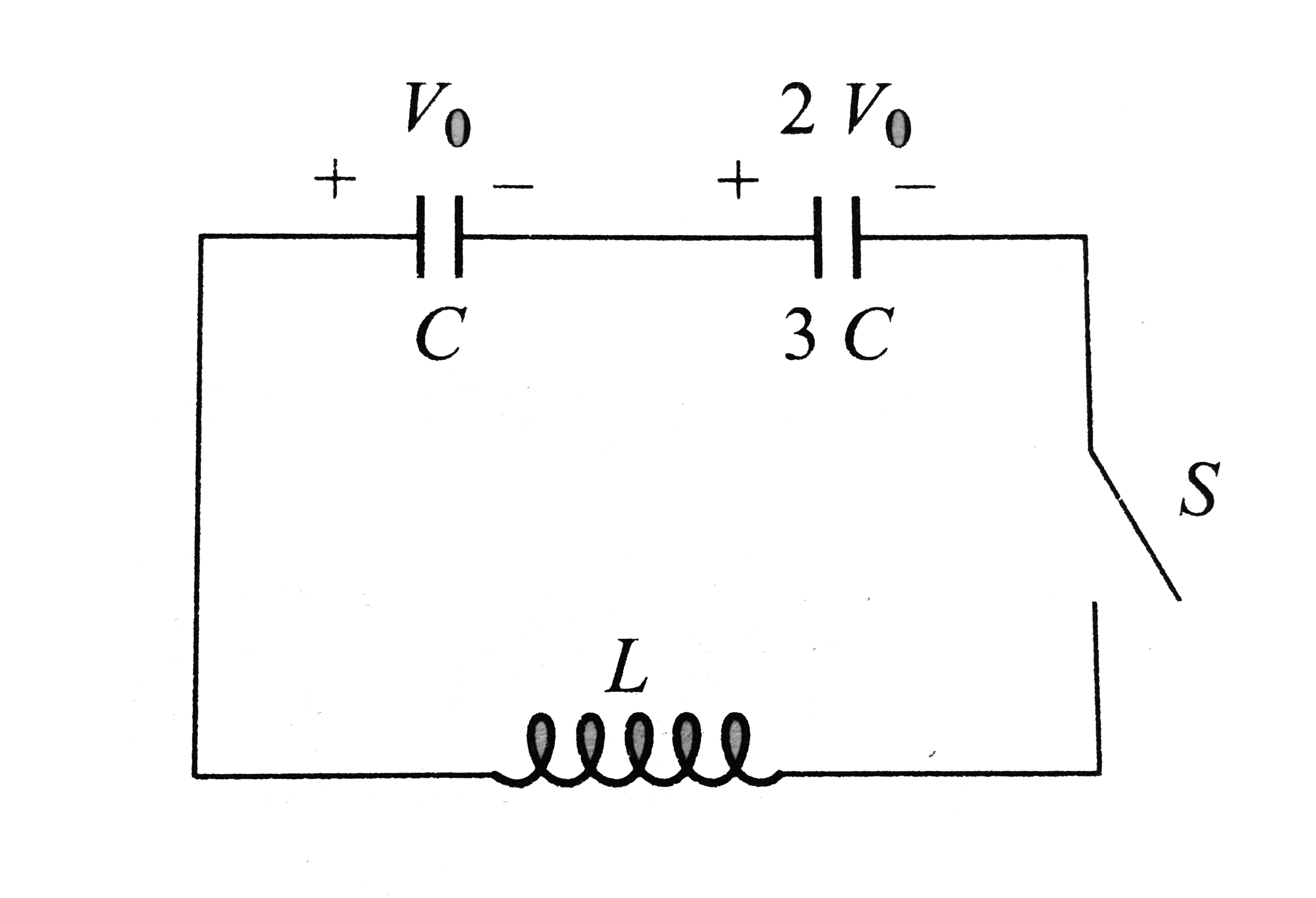
The maximum current in the inductor is
View SolutionTwo capacitors 2C and 4C initially charged to potential difference of V0and3V0 with the potential as show are connected to an inductor of inductance L. Initial curren tin the inductor is zer. Now the swtich 'S' is closed. The maxmimum current in the circuit is
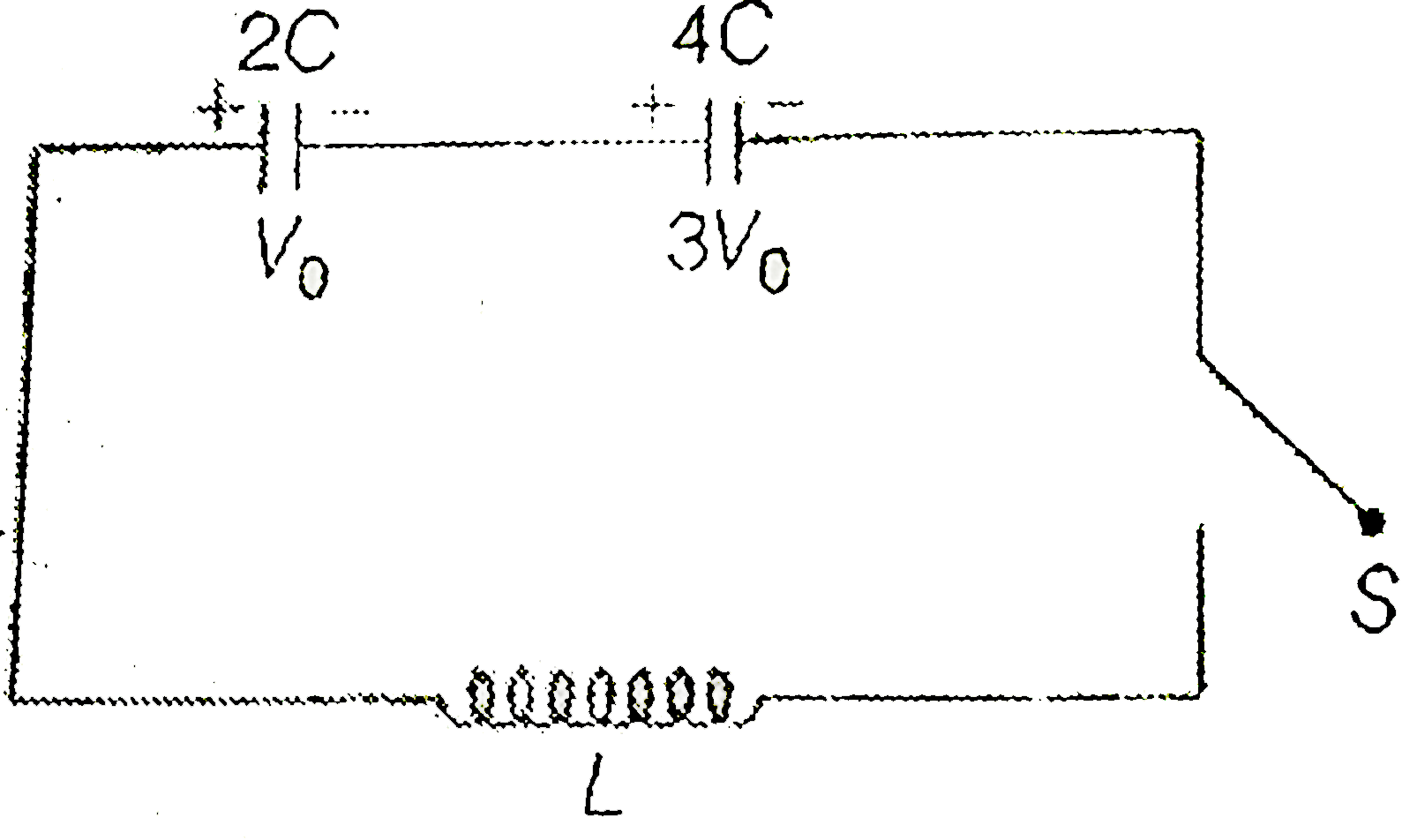
View Solution
Knowledge Check
A condenser of capacity C is charged to a potential difference of V1. The plates of the condenser are then connected to an ideal inductor of inductance L. The current through the inductor when the potential difference across the condenser reduces to V2 is
A(C(V1−V2)2L)12BC(V21−V22)LCC(V21+V22)LD(C(V21−V22)L)12
A capacitor of capacitnace C is charged to a potential difference V and then disconnected from the battery. Now it is connected to an inductor of inductance L at t=0. Then

View SolutionTwo capacitors with capacities C1 and C2 ,are charged to potentials V1 and V2 respectively.When they are connected in parallel,the ratio of their respective charges is ....?
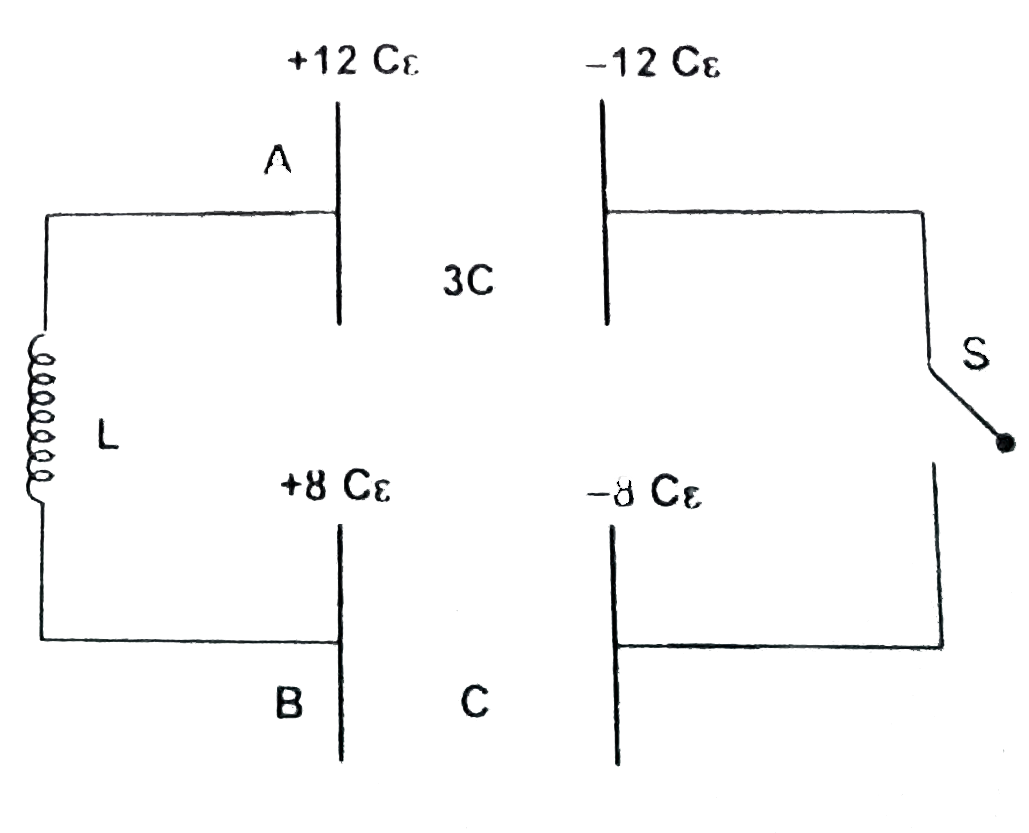
View SolutionIn the adjacent circuit, the capacitor 'A' of capacitance '3C' and the capacitor 'B' of capacitance 'C' are initially charged by potential drops 4ɛ and 8ɛ respectively and connected through and inductor of inductance 'L' with zero initial current as shown. The switch 'S' is closed at t=0. then the maximum current through the inductor is
View SolutionA condenser of capacity C is charged to a potential difference of V1. The plates of the condenser are then connected to an ideal inductor of inductance L. The current through the inductor wehnn the potential difference across the condenser reduces to V2 is
View SolutionA capacitor of capacitance C1 is charged to a potential difference V and then connected with an uncharged capacitor of capacitance C2 a resistance R. The switch is closed at t = 0. Choose the correct option(s):
View SolutionAn ideal capacitor of capacitance 0.2μF is charged to a potential difference of 10V. The charging battery is than disconnected. The capacitor is then connected to an ideal inductor of self inductance 0.5mH. The current at a time when the potential difference across the capacitor is 5V is :
View SolutionA capacitor of capacity 2μF is charged to a potential difference of 12V. It is then connected across an inductor of inductance 6μH. At an instant when potential difference across the capacitor is 6V, what is the current(in A)?
View Solution
