In the given at t=0, switch S is closed.
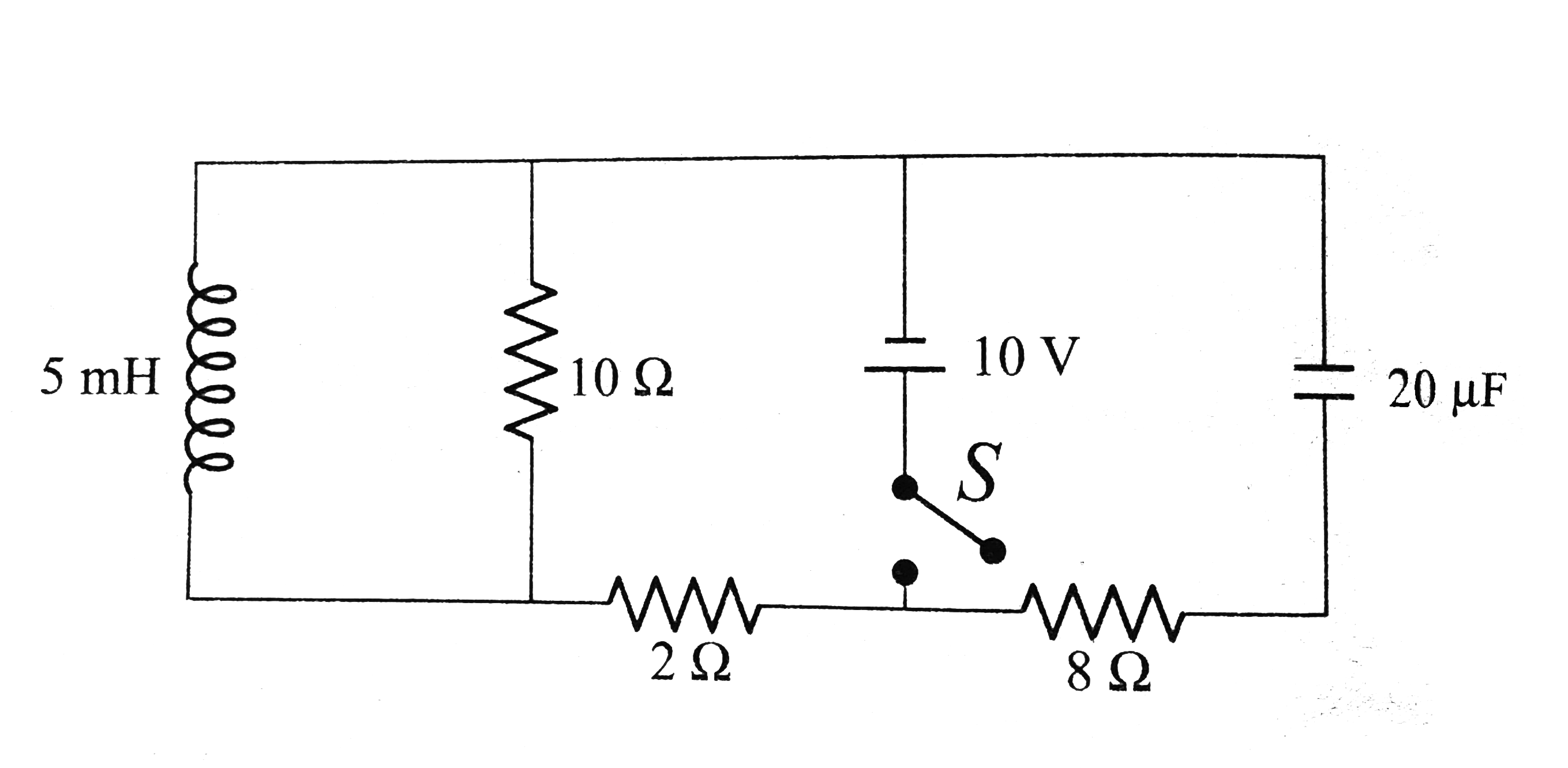
The energy stored in the capacitor and inductor, respectively, at t→∞ will be
1mJ and 62.5mJ
62.5mJ and 1mJ
2mJ and 62.5mJ
1mJ and 60mJ
The correct Answer is:A
From loop, applying kirchhoff's law,
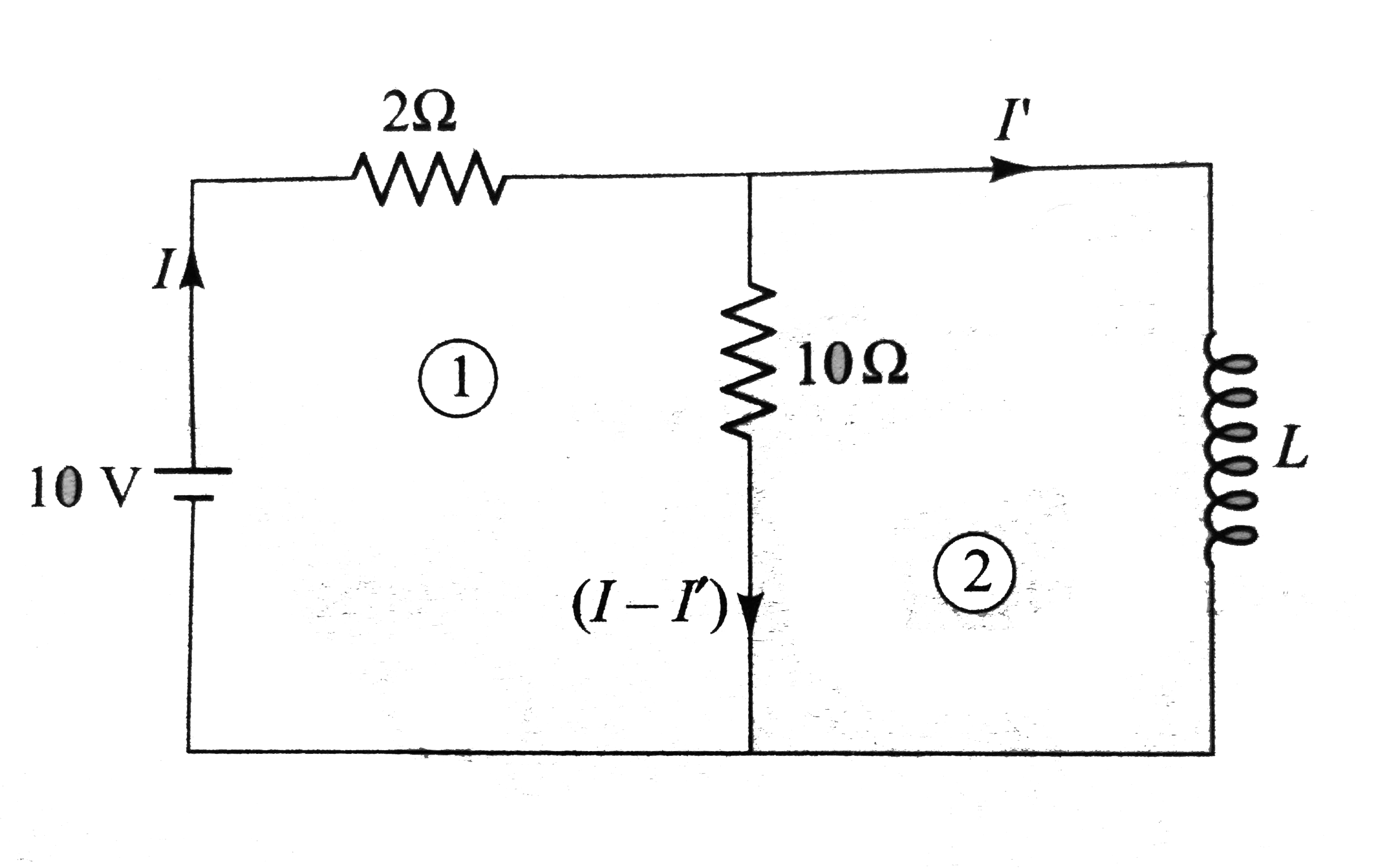
12I−10I'=10
From loop (ii) (i)
−LdI'dt+10I−10I'=0
I−I'=L10dI'dt (ii)
Solving simultaneously (i) and (ii), we have
I'=5−5e−5t3L (iii)
and I=5−256e−5t3L (iv)
I−I'=56e−1000t3
EL=12L(I')2,EL=1252(1−e−1000tL)2mJ
Current in the inductor at t=∞,I'=5A
EL(t→∞)=12×5×10−3(5)2
EL=62.5mJ
EC(t→∞)=12CV2=12×20×10−6×100=1mJ
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Exercises (integer)8videos
INDUCTANCE
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Archives (fills In The Blanks)3videos
INDUCTANCE
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Exercises (assertion-reasoning)2videos
INDUCTANCE
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit27videos
HEATING EFFECT OF CURRENT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type2videos
MAGNETIC FIELD AND MAGNETIC FORCES
Similar Questions
In the given at t=0, switch S is closed.
The energy stored in the inductor at any instant t(0<t∞) will beView Solution
In given LR circuit the switch S is closed at time t=0 thenView SolutionIn the given at t=0, switch S is closed.
The current through the 10Ω resistor at any instant t(0<t<∞) will beView SolutionIn the circuit shown if Fig. the switch S is closed at time t = 0. The current through the capacitor and inductor will be equal at time t equal (given R=√L/C
 View Solution
View SolutionIn the given circuit Fig the switch is closed at t=0. Choose the correct answers.
 View Solution
View SolutionSwitch is closed at t=0 then the current in the circuit at t=L2R is
_PHY_E06_157_Q01.png) View Solution
View SolutionIn given circuit when switch S has been closed, then charge on capacitor A and B respectively
 View Solution
View SolutionIn the given circuit, the switch S is closed at time t = 0 . The charge Q on the capacitor at any instant t is given by Q(t)=Q(1−e−αt). Find the value of Q0 and α in terms of given parameters as shown in the circuit.
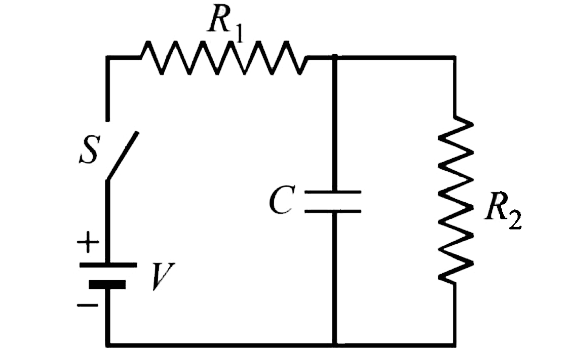 . View Solution
. View SolutionA capacitor of capacitance Chas initial charge Q0 and connected to an inductor L as shown. Att=0 switch S is closed. The current through the inductor when energy in the capacitor is three times the energy of inductor is
 View Solution
View SolutionA charge Q is given to the plates of an isolated capacitor of capacitance C. Now, the terminals of this capacitor are connected to the terminals of an inductor L at t = 0. After how much time will the energy stored in the capacitor and the Inductor become equal?
View Solution
