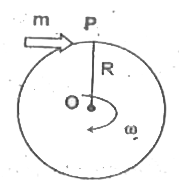
A bullet of mass m collides inelastically at the periphery of a disc of mass M and radius R, with a speed v as shown. The disc rotates about a fixed horizontal axis. Find the angular velocity of the disc bullet system just after the impact.

In this impact, the torque caused by the impulsive forces acting about the centr O is zero as for the system of bullet and disc impact force is internal force.
That is why we can conserve the angular momentum of the system about the axis passing through O just before and after the impact. The angular momentum of the system about O, is
where = M.I. of the system about
Using (A1) & (2) we obtain
Similar Questions
A point mass m collides with a disc of mass m and radius R resting on a rough horizontal surface as shown . Its collision is perfectly elastic. Find angular velocity of the disc after pure rolling starts

View SolutionA disc of mass M and Radius R is rolling with an angular speed ω on the horizontal plane. The magnitude of angular momentum of the disc about origin is:
View SolutionA disc of mass m and radius R moves in the x−y plane as shown in Fig. The angular momentum of the disc about the origin O at the instant shown is

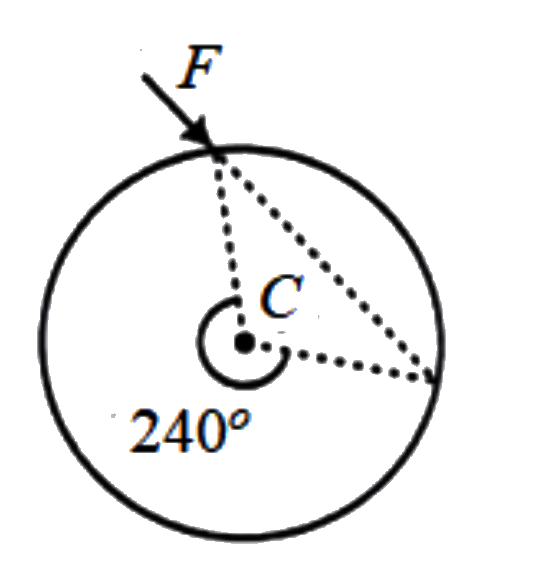
View SolutionA uniform disc of mass M and radius R is hinged at its centre C . A force F is applied on the disc as shown . At this instant , angular acceleration of the disc is
View SolutionA disc of mass m has a charge Q distributed on its surface. It is rotating about an XX' with a angular velocity ω. The force acting on the disc is
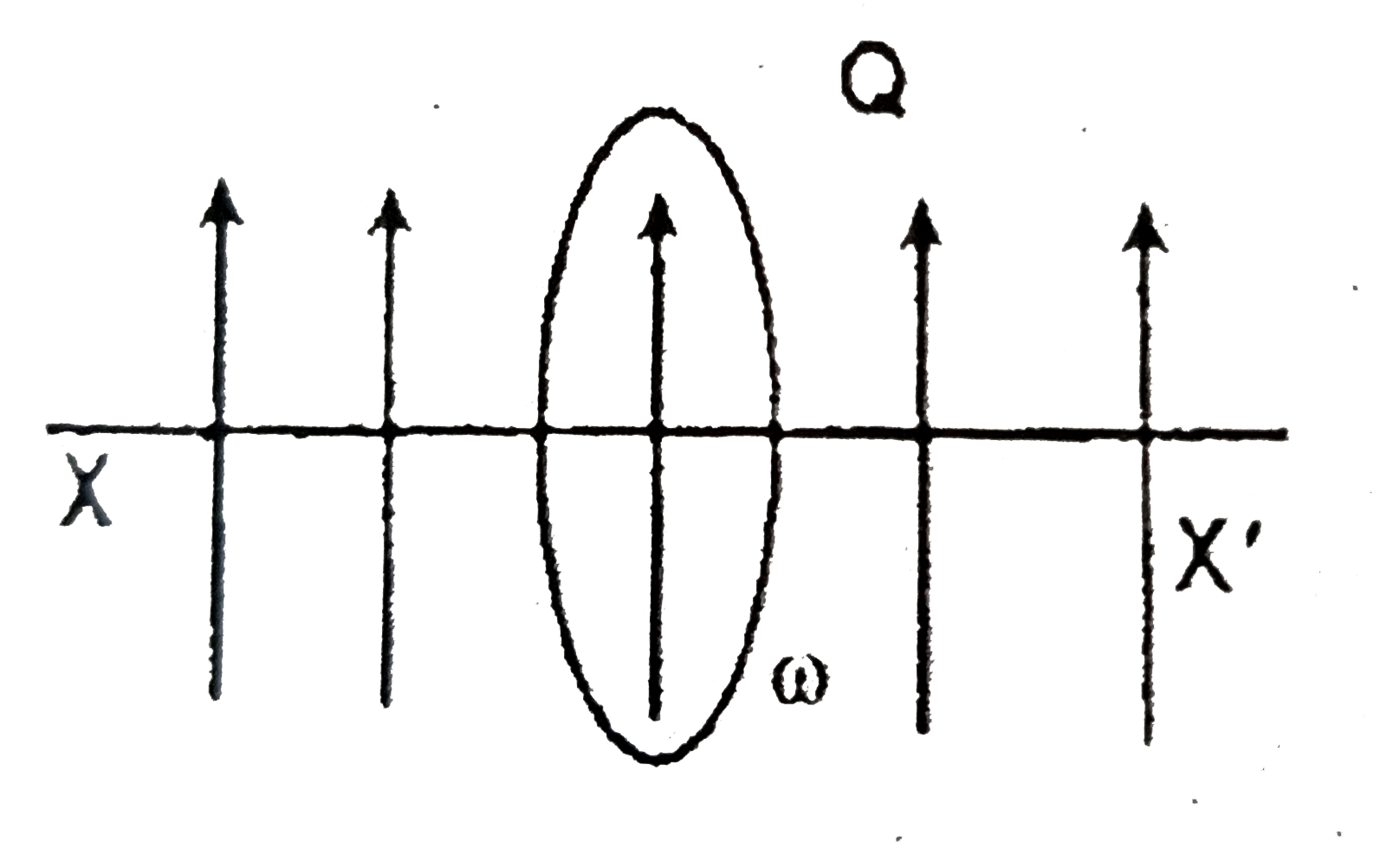
View SolutionA small hole is made in a disc of mass M and radius R at a distance R/4 from centre. The disc is supported on a horizontal peg through this hole. The moment of inertia of the disc about horizontal peg is
View SolutionThree forces of magnitude F, F and √2F are acting on the periphery of a disc of mass m and radius R as shown in the figure. The net torque about the centre of the disc is
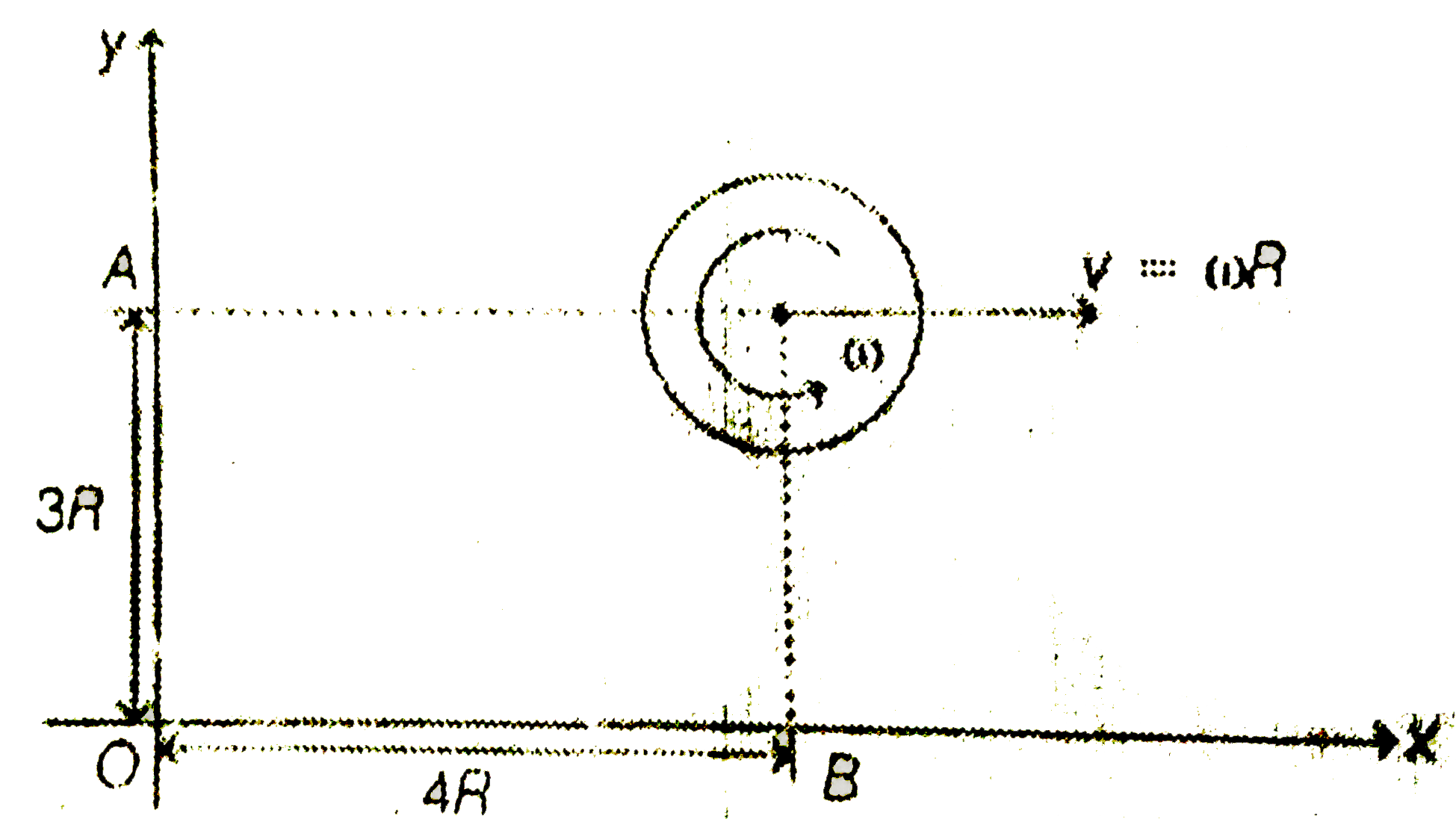
View SolutionA disc of mass M and radius R moves in the x-y plane as shown in the figure. The angular momentum of the disc at tihe instant shows is
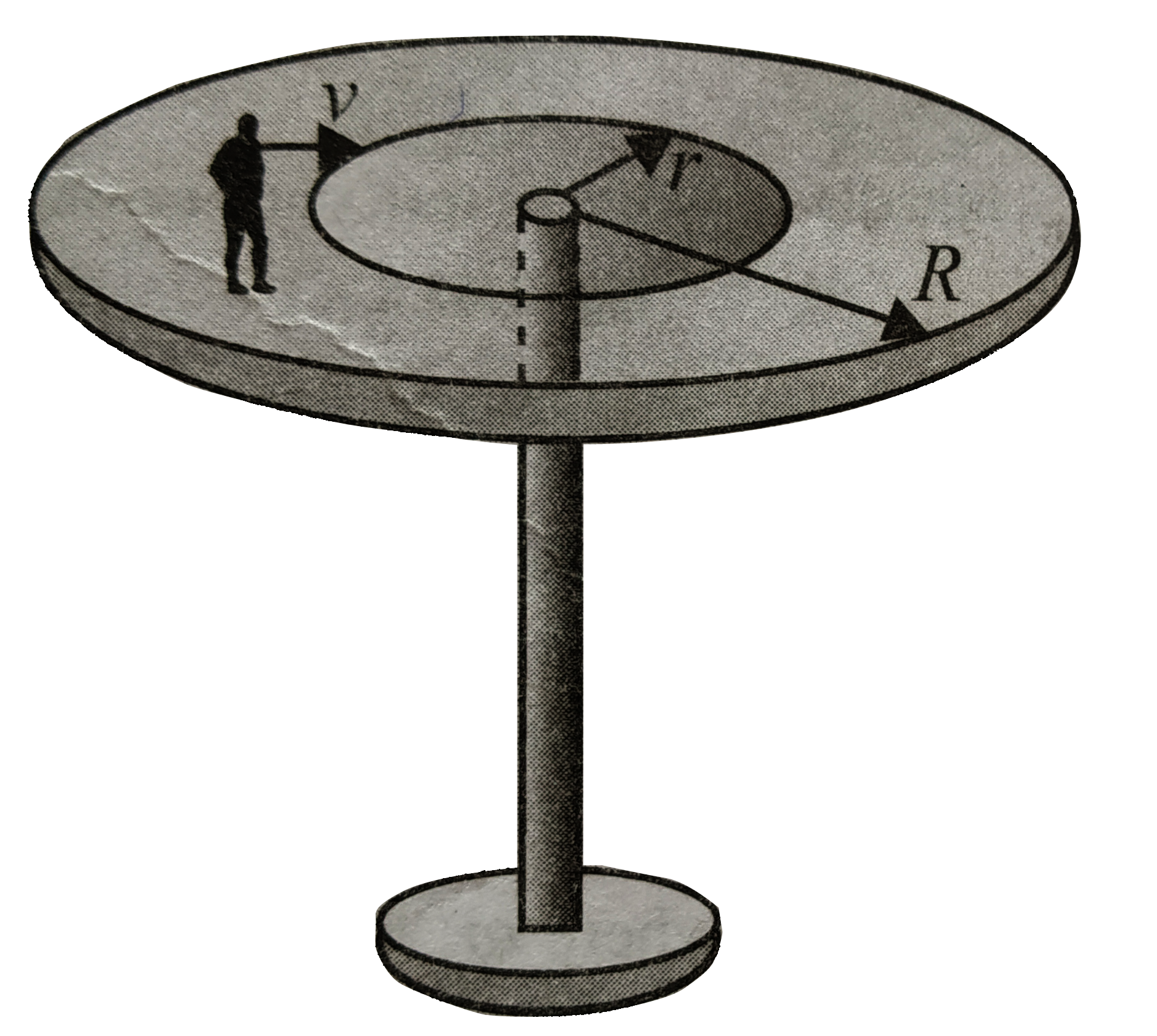
View SolutionA man of mass m stands on a horizontal platform in the shape of a disc of mass m and radius R, pivoted on a vertical axis thorugh its centre about which it can freely rotate. The man starts to move aroung the centre of the disc in a circle of radius r with a velocity v relative to the disc. Calculate the angular velocity of the disc.
View SolutionA particle of mass 'm' is attached to the rim of a uniform disc of mass 'm' and radius R. The disc is rolling wihtout slipping on a stationery horizontal surface as shown in the figure. At a particular instant, the particle is at the topmost position and centre of the disc has speed v0 amd its angular speed is ω. Choose the correct option (s).
View Solution

