A man of mass m stands on a horizontal platform in the shape of a disc of mass m and radius R, pivoted on a vertical axis thorugh its centre about which it can freely rotate. The man starts to move aroung the centre of the disc in a circle of radius r with a velocity v relative to the disc. Calculate the angular velocity of the disc.

Since there is no torque acting about the axis of rotation of the disc, so the angular momentum of the system (disc+man) remains constant. Initially it is zero. Suppose ω is the angular velocity of the disc (take positive in the sense of motion of the man). The velocity of the man with respect to the ground observer will be:
→vman, disc=→vman−→v(disc)
⇒→vman=→v(man,disc)−→vdisc
or →vman=v−ωr
Thus, angular momentum of the man =m(v−ωr)r
And angular momentum of the disc is
Idiscω=MR22ω
By conservation of angular momentum, we have
m(v−ωr)=MR22ω
After solving, we get ω=mvr(mvr2+MR22)
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICS ENGLISHChapter:RIGID BODY DYNAMICS 2Exercise:Solved Examples
Explore 12 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICS ENGLISHChapter:RIGID BODY DYNAMICS 2Exercise:Exercise 3.1
Explore 11 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICS ENGLISHChapter:RIGID BODY DYNAMICS 1Exercise:Integer
Explore 11 Videos
- SOUND WAVES AND DOPPLER EFFECTBook:CENGAGE PHYSICS ENGLISHChapter:SOUND WAVES AND DOPPLER EFFECTExercise:Integer
Explore 16 Videos
Similar Questions
A disc of radius r is removed from the centre of a disc of mass M and radius R. The M.I. About the axis through the centre and normal to the plane will be:
View Solution
A uniform disc of mass M and radius R is pivoted about the horizontal axis through its centre C A point mass m is glued to the disc at its rim, as shown in figure. If the system is released from rest, find the angular velocity of the disc when m reaches the bottom point B.
View SolutionThe moment of inertia of a disc of mass M and radius R about an axis. Which is tangential to sircumference of disc and parallel to its diameter is.
View SolutionA uniform disc of mass m and radius R rotates about a fixed vertical axis passing through its centre with angular velocity ω. A particle of same mass m and having velocity of 2ωR towards centre of the disc collides with the disc moving horizontally and sticks to its rim. Then
View SolutionA thin uniform circular disc of mass M and radius R is rotating in a horizontal plane about an axis passing through its centre and perpendicular to its plane with an angular velocity ω . Another disc of same dimensions but of mass 14 M is placed gently on the first disc co-axially. The angular velocity of the system is
View SolutionA bullet of mass m collides inelastically at the periphery of a disc of mass M and radius R, with a speed v as shown. The disc rotates about a fixed horizontal axis. Find the angular velocity of the disc bullet system just after the impact.

View SolutionA uniform disc of radius R rolls perfectly over two horizontal plank A and B moving with velocities v and 2v, spectively. Find the
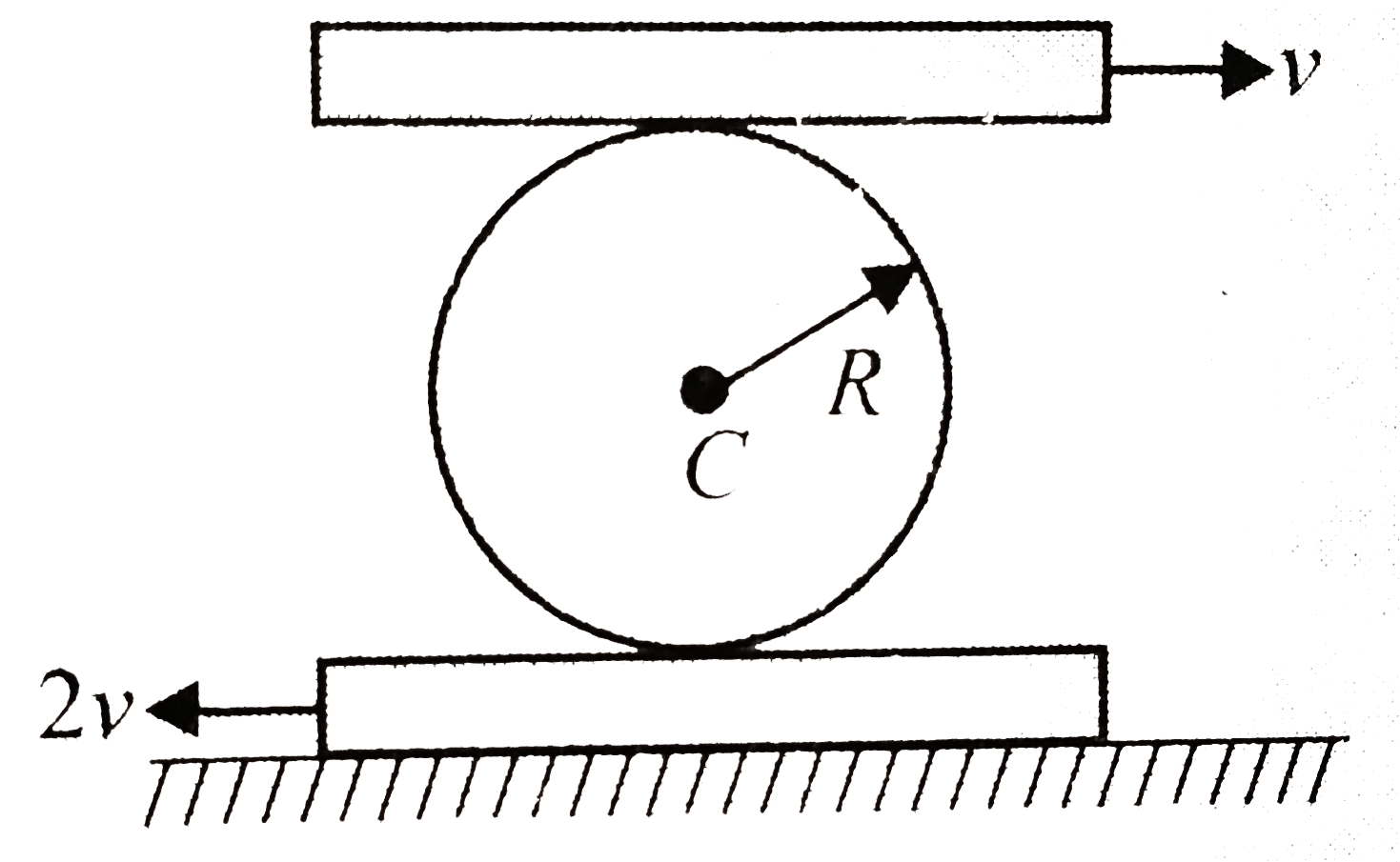
a. velocity of CM of the disc.
b. angular velocity of the disc.
View SolutionA thin uniform circular disc of mass M and radius R is rotating in a horizontal plane about an axis passing through its centre and perpendicular to its plane with an angular velocity ω. another disc of the same dimensions but of mass M/4 is placed gently on the first disc coaxially. The angular velocity of the system now is 2ω/√5.
View SolutionA horizontal disc is rotating about a vertical axis passing through its centre. If an insect moves from centre to rim then the angular momentum of the system
View SolutionA uniform circular disc of mass M and radius R is pivoted at distance x above the centre of mass of the disc, such that the time period of the disc in the vertical plane is infinite. What is the distance between the pivoted point and centre of mass of the disc ?
View Solution