A uniform rod of length L pivoted at the bottom of a pond of depth L/2 stays in stable equilibrium as shown in the figure.

Find the angle θ if the density of the material of the rod is half of the density of water.
(a) Weight of the rod W = LAρ g
(A = area of cross section, ρ = density of material)
Submerged length of the rod
OT=L2sinθ
Buoyant force, B=(L2sinθ)Aρwg
(from Archimedies principle) (ρw = density of water)
This acts at P, where OP=OT2=l4sinθ
Balancing torque about O
W.OQcosθ=B.OPcosθ
(LAρg)L/2=(L2sinθ)Aρwg(L4sinθ)
sin2θ=ρw4ρ
⇒ sin2θ=1/2⇒θ=45∘
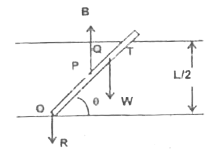
(b) Also, balancing forces
R + W = B
R=B−W=ρAρwg2sinθ−LAρg
=LAρg[1sinθ−1] (∵ρw=2ρ)
=(√2−1)mg
Similar Questions
A uniform rod of length L pivoted at the bottom of a pond of depth L/2 stays in stable equilibrium as shown in the figure.

Find the angle 0 if the density of the material of the rod is half of the density of water.
View SolutionA uniform rod of length L pivoted at the bottom of a pond of depth L/2 stays in stable equilibrium as shown in the figure.

Find the force acting at the pivoted end of the rod in terms of mass m of the rod.
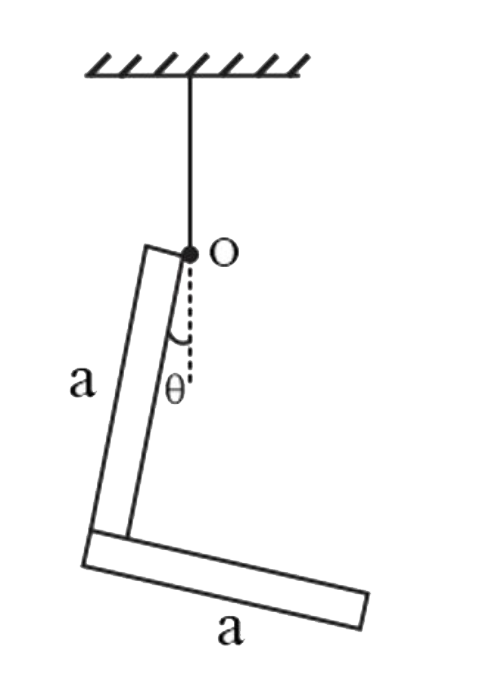
View SolutionA uniform L shaped rod each of side a is held ,as shown in the figure. The angle θ such that rod remains stable. Will be.
View SolutionFind the rate of heat flow through a cross section of the rod shown in figure (θ2>θ1) . Thermal conductivity of the material of the rod is K.

View SolutionA uniform rod of mass m and length L is kept on a horizontal table with L4 length on the table as shown in figure. As the string attached to the end B is cut, the angular acceleration of the rod about point C will be
_PHY_E05_242_Q01.png)
View SolutionTwo uniform thin rods each of length L and mass m are joined as shown in the figure. Find the distance of centre of mass the system from point O

View SolutionA rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What is the rate of change of angular momentum of the rod ?

View SolutionA uniform rod of length l and mass m is hung from, strings of equal length from a ceiling as shown in figure. Determine the tensions in the strings?

View SolutionA rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What angle will the rod make with the vertical

View SolutionFigure shows a rigid rod of length 1.0 m. It is pivoted at O. For what value m, the rod will be in equilibrium ? Find the force (F) exerted on the rod by the pivot. Neglect the weight of the rod.
View Solution