A uniform rod of length L pivoted at the bottom of a pond of depth L/2 stays in stable equilibrium as shown in the figure.

Find the force acting at the pivoted end of the rod in terms of mass m of the rod.
(√2−1)mg
(√2+1)mg
(√3+1)mg
(√2+3)mg
The correct Answer is:A
Weight of the rod w=LAρg
(A=area of cross section ρ=density of material)
Submerged length of the given by
OT=L2sinθ
Buoyant force B=(L2sinθ)Aρwg
From Archimedes' principle (ρw= density of water).
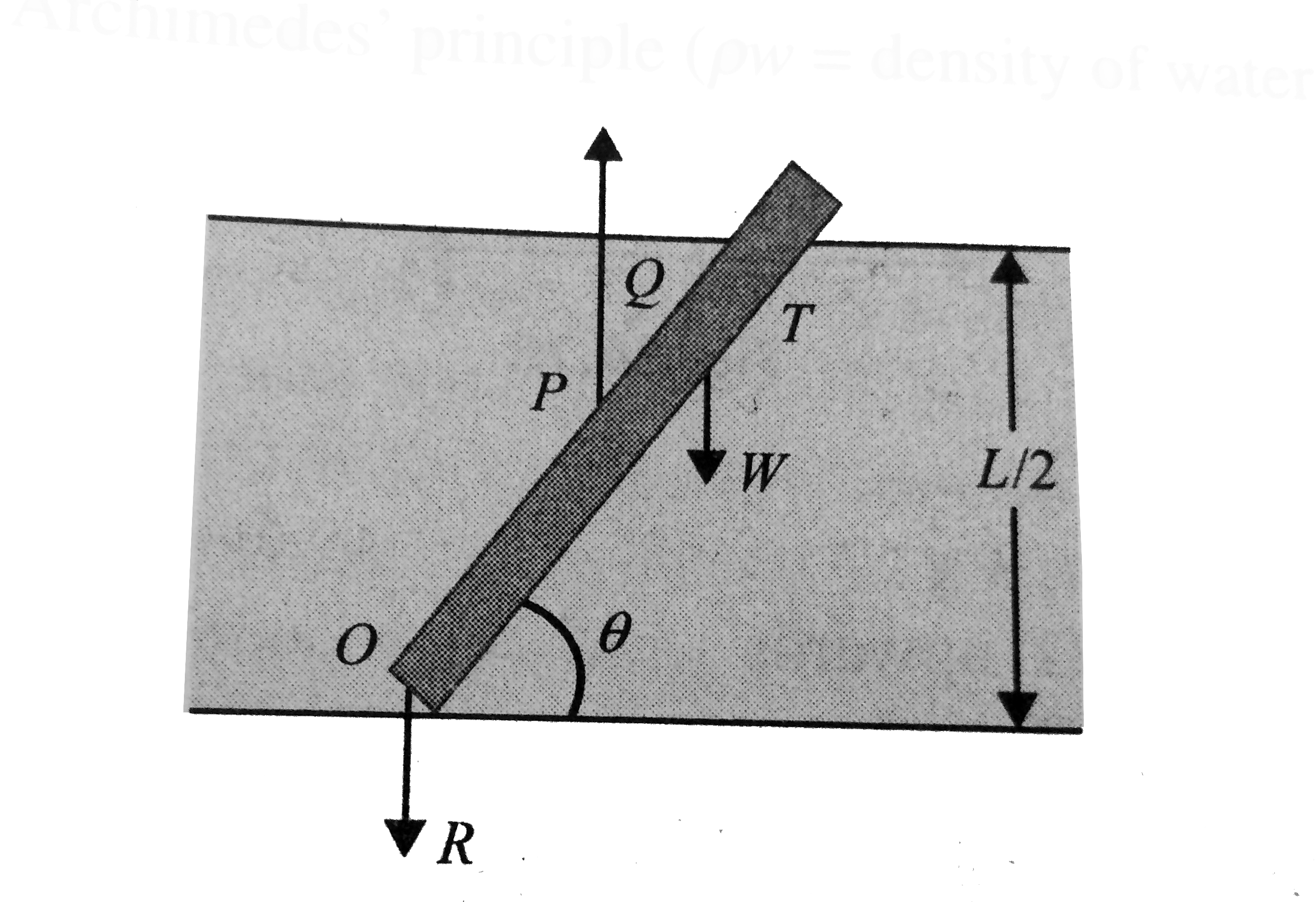
This force acts at P, where OP=OT2=l4sinθ
Balancing torque about O is
WOQcosθ=BOPcosθ
(LAρg)L2=(Lsinθ)Aρwg(L4sinθ)
sin2θ=ρw4ρ⇒sin2θ=12⇒θ=45∘
Also balancing forces R+W=B
R=B−W=ρAρwg2sinθ−LAρg
=LAρg[1sinθ−1] (∵ρw=2ρ)=(√2−1)mg
Topper's Solved these Questions
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:True/False
Explore 1 Video
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:SCQ_TYPE
Explore 13 Videos
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:Assertion-Reasoning
Explore 8 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICSChapter:DIMENSIONS & MEASUREMENTExercise:Integer
Explore 2 Videos
- GRAVITATIONBook:CENGAGE PHYSICSChapter:GRAVITATIONExercise:INTEGER_TYPE
Explore 1 Video
Similar Questions
A ligh rod of length 1 m is pivoted at its centre and two masses of 5 kg and 2 kg are hung from the ends as shown in the figure. Find the initial angular acceleration of the rod assuming that it was horizontal in the beginning.

View SolutionA uniform slender rod of mass M and length L is pivoted at its end. The rod is released from its nearly vertical position. What is the reaction at the pivot when the rod reaches the horizontal position? If the support is withdrawn at this instant, describe the subsequent motion of the rod.
View Solution
Knowledge Check
A uniform rod of length L pivoted at the bottom of a pond of depth L/2 stays in stable equilibrium as shown in the figure.

Find the angle 0 if the density of the material of the rod is half of the density of water.A60∘B30∘C45∘D37∘A uniform rod of mass m length l is attached to smooth hinge at end A and to a string at end B as shown in figure. It is at rest. The angular acceleration of the rod just after the string is cut is :
 A3g2lB3g4lC5g4lD5g2l
A3g2lB3g4lC5g4lD5g2l
A uniform rod of length L and mass m is free to rotate about a frictionless pivot at one end as shown in figure. The rod is held at rest in the horizontal position and a coin of mass m is placed at the free end. Now the rod is released The reaction on the coin immediately after the rod starts falling isA3mg2B2mgCzeroDmg2
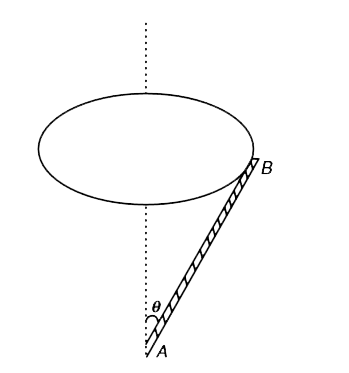
A uniform rod of mass m and length L is fixed to an axis, making an angle θ with it as shown in the figure. The rod is rotated about this axis so that the free end of the rod moves with a uniform speed ‘v’. Find the angular momentum of the rod about the axis. Is the angular momentum of the rod about point A constant?
View SolutionA uniform rod of length L and mass M is lying on a frictionless horizontal plane and is pivoted at one of its ends as shown in Fig. There is no friction at the pivot. An inelastic ball of mass m is fixed with the rod at a distance L/3 from O. A horizontal impulse J is given to the rod at a distance 2L/3 from O in a direction perpendicular to the rod. Assume that the ball remains in contact with the rod after the collision and impulse J acts for a small time interval △t. Now answer the following questions:

Find the resulting instantaneous angular velocity of the rod after the impulse.
View SolutionA uniform rod of length L and mass M is lying on a frictionless horizontal plane and is pivoted at one of its ends as shown in Fig. There is no friction at the pivot. An inelastic ball of mass m is fixed with the rod at a distance L/3 from O. A horizontal impulse J is given to the rod at a distance 2L/3 from O in a direction perpendicular to the rod. Assume that the ball remains in contact with the rod after the collision and impulse J acts for a small time interval △t. Now answer the following questions:

Find the impulse acted on the ball during the time △t
View SolutionA uniform rod of length L and mass M is lying on a frictionless horizontal plane and is pivoted at one of its ends as shown in Fig. There is no friction at the pivot. An inelastic ball of mass m is fixed with the rod at a distance L/3 from O. A horizontal impulse J is given to the rod at a distance 2L/3 from O in a direction perpendicular to the rod. Assume that the ball remains in contact with the rod after the collision and impulse J acts for a small time interval △t. Now answer the following questions:

Find the magnitude of the impulse applied by the during the time interval △t
View SolutionA rod of length L and mass M is acted on by two unequal forces F1 and F2(<F)as shown in the figure.
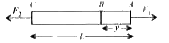
The tension in the rod at a distance y from the end A is given by
View Solution

