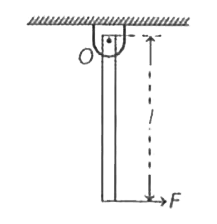
A uniform rod of mass m and length l is pivoted smoothly at point O as shown in figure. If a horizontal force F acts at the bottom of the rod and $ω$ is the angular velocity of the rod which is a function of angle of rotation $θ$ , then the maximum angular displacement of the rod is
(Acceleration due to gravity, g)
Solution in Telugu

A

$θ = 2 \sin^{- 1} (\frac{2 F}{m g})$

B

$θ = 2 \cos^{- 1} (\frac{2 F}{m g})$

C

$θ = 2 \tan^{- 1} (\frac{2 F}{m g})$

D

$θ = 2 \cot^{- 1} (\frac{2 F}{m g})$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

According to the question, we drawn the following figure,

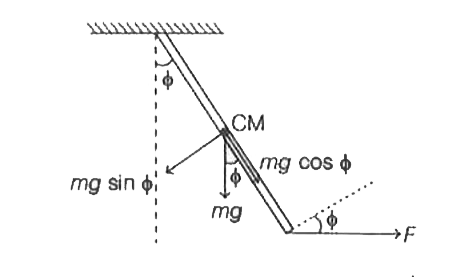
As for maximum angular displacement, equilibrium of torque exists about the centre mass of rod.
So, $τ_{1} + τ_{2} = 0 …(i)$
Torque due to the gravitational force,
$τ_{1} = m g \sin ϕ \times 1$
$\Rightarrow τ_{1} = m g l \sin ϕ ...(ii)$
Similarly, torque due to horizontal force,
$τ_{2} = - F 2 l \cos ϕ$
$\Rightarrow τ_{2} = 2 F l \cos ϕ ...(iii)$
From Eqs. (i), (ii) and (iii), we get
$\tan ϕ = \frac{2 F}{m g} \Rightarrow ϕ = \tan^{- 1} \frac{2 F}{m g}$
Since, the angular velocity of the rod is a function of angle of rotation $θ$ ,
As putting, $θ_{max} = 2 ϕ$
So, $ϕ = \frac{θ_{max}}{2}$
Hence, $θ_{max} = 2 \tan^{- 1} \frac{2 F}{m g}$
The correct option is (c).

Updated on:21/07/2023

|

Class 12 PHYSICS AP EAMCET SOLVED PAPER 2019 (22-04-2019, SHIFT-2)

Topper's Solved these Questions

Similar Questions

TS EAMCET PREVIOUS YEAR PAPERS-AP EAMCET SOLVED PAPER 2019 (22-04-2019, SHIFT-2)-PHYSICS

Home
Ask Doubt
Profile