A cube of mass m and density D is suspended from a point P by a spring of stiffness k. The system is kept inside a beaker filled with a liquid of density d. The elongation in the spring, assuming D>d, is :

mgk(1−dD)
mg1(1−Dd)
mgk(1+dD)
None of these
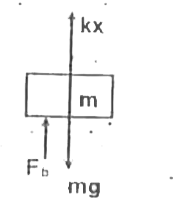
The cube is in equilibrium under the following three forces ,
spring force kx , where x = elongation of the spring ,
gravitional force w , weight of the cube = mg
buoyant force Fb ( or upward thrust ) imparted by the liquid on the cube given as Fb=Vdg where V = volume of the immersed portion of the cube equilibrium of the cube , kx+Fb=mg
⇒x=mg−Fbk=mg−Vdgk where V = volume he immersed portion of the cube , For complete immersion , V = volume of the cube
For equilibrium of the cube , kx+Fb=mg
⇒=mg−Fbk=mg−Vdgk Where V = (m/D)
⇒x=mgk(1−dD)
Hence (A) is correct
Similar Questions
A block of mass m suspended from a spring of spring constant k. Find the amplitude of S.H.M.
View SolutionA vessel filled with water is kept on a weighing pan and the scale adjusted of zero. A block of mass M and density ρ is suspended by a masselss spring of spring constant k. This block is submerged inside into the water in the vessel. What is the reading of the scale /
View Solution
Knowledge Check
A uniform cylinder of length L and mass M having cross-sectional area A is suspended, with its length vertical, from a fixed point by a massless spring such that it is half submerged in a liquid of density σ at equilibrium position. The extension x0 of the spring when it is in equlibrium is:
AMgk(1+LaσM)BMgkCMgk(1+LaσM)DMgk(1−Laσ2M)
A rod mass (M) hinged at (O) is kept in equilibrium with a spring of stiffness (k) as shown in figure. The potential energy stored in the spring is .

View SolutionA mass M is suspended as shown in fig. The system is in equilibrium. Assume pulleys to be massless. K is the force constant of the spring.
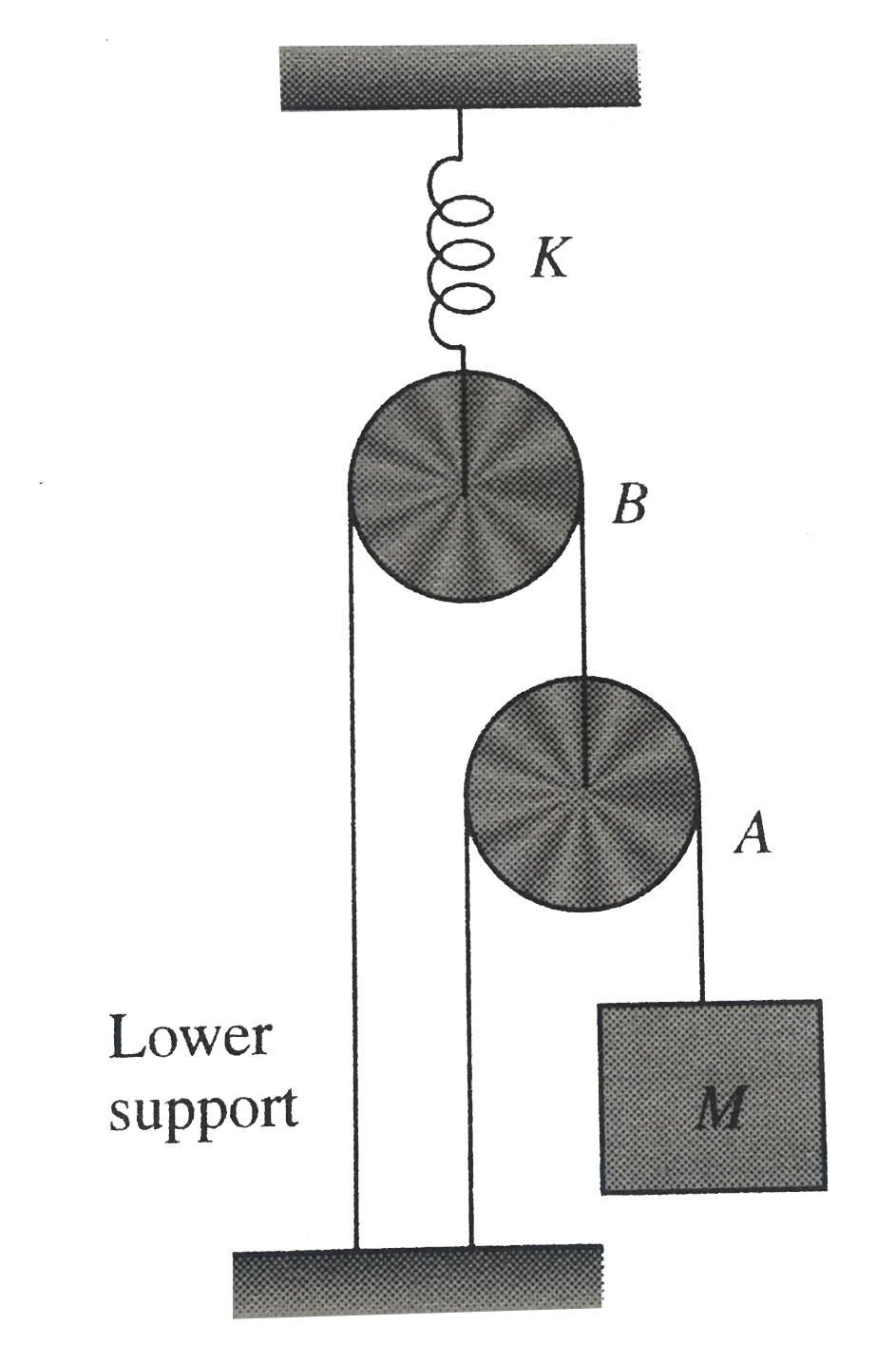
The extension produced in the spring is given by
View SolutionA block of mass m is suddenly released from the top of a spring of stiffness constant k.
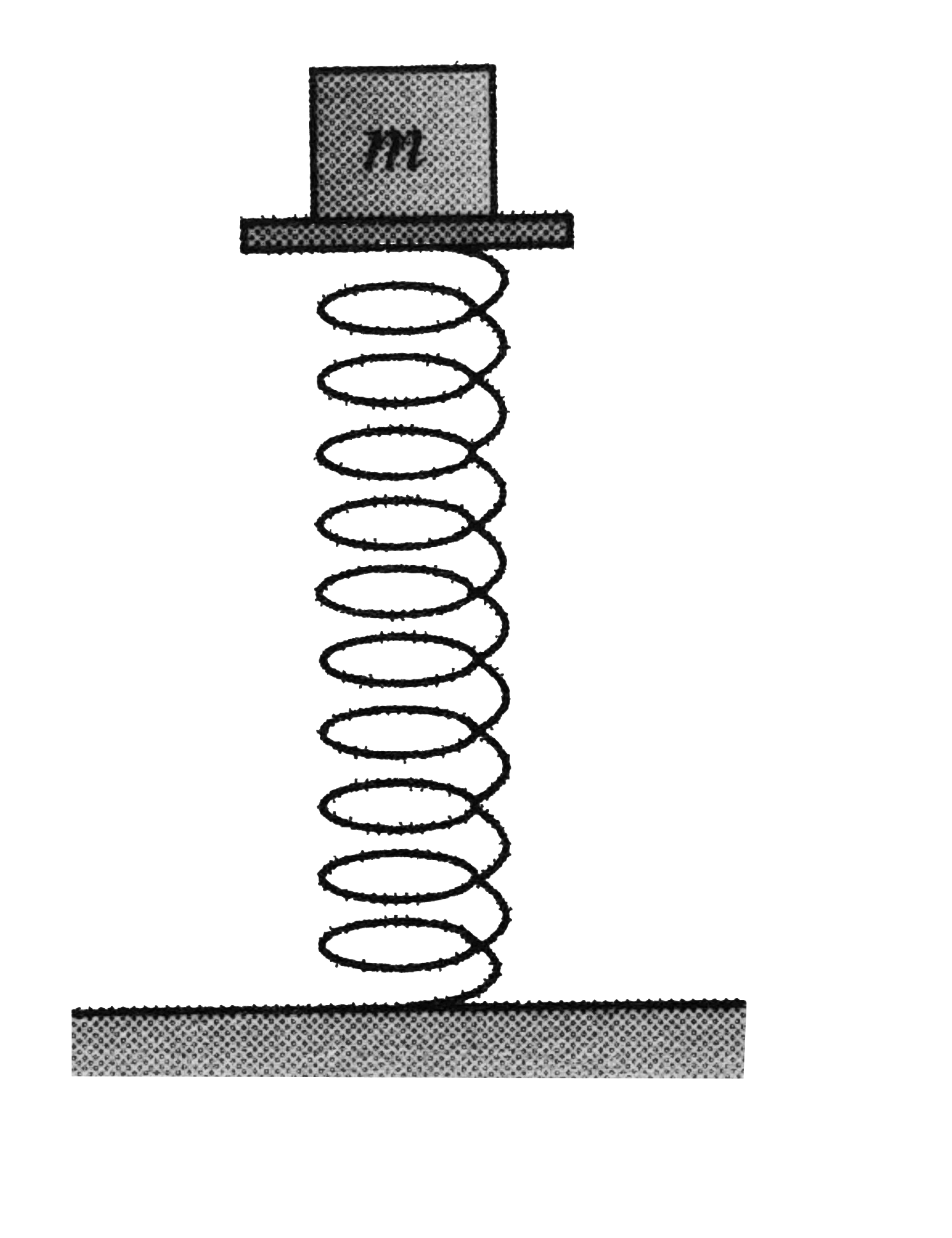
a. Find the acceleration of block just after release.
b. What is the compression in the spring at equilibrium.
c. What is the maximum compression in the spring.
d. Find the acceleration of block at maximum compression in the spring.
View SolutionA uniform cylinder of length L and mass M having cross-sectional area A is suspended, with its length vertical, from a fixed point by a massless spring such that it is half submerged in a liquid of density σ at equilibrium position. The extension x0 of the spring when it is in equlibrium is:
View SolutionA mass m is vertically suspended from a spring of negligible mass, the system oscillates with a frequency n. what will be the frequency of the system, if a mass 4m is suspended from the same spring?
View SolutionTwo identicle particles A and B, each of mass m, are interconnected by a spring of stiffness k. If particle B experiences a forec F and the elongation of the spring is x, the acceleration of particle B relative to particle A is equal to

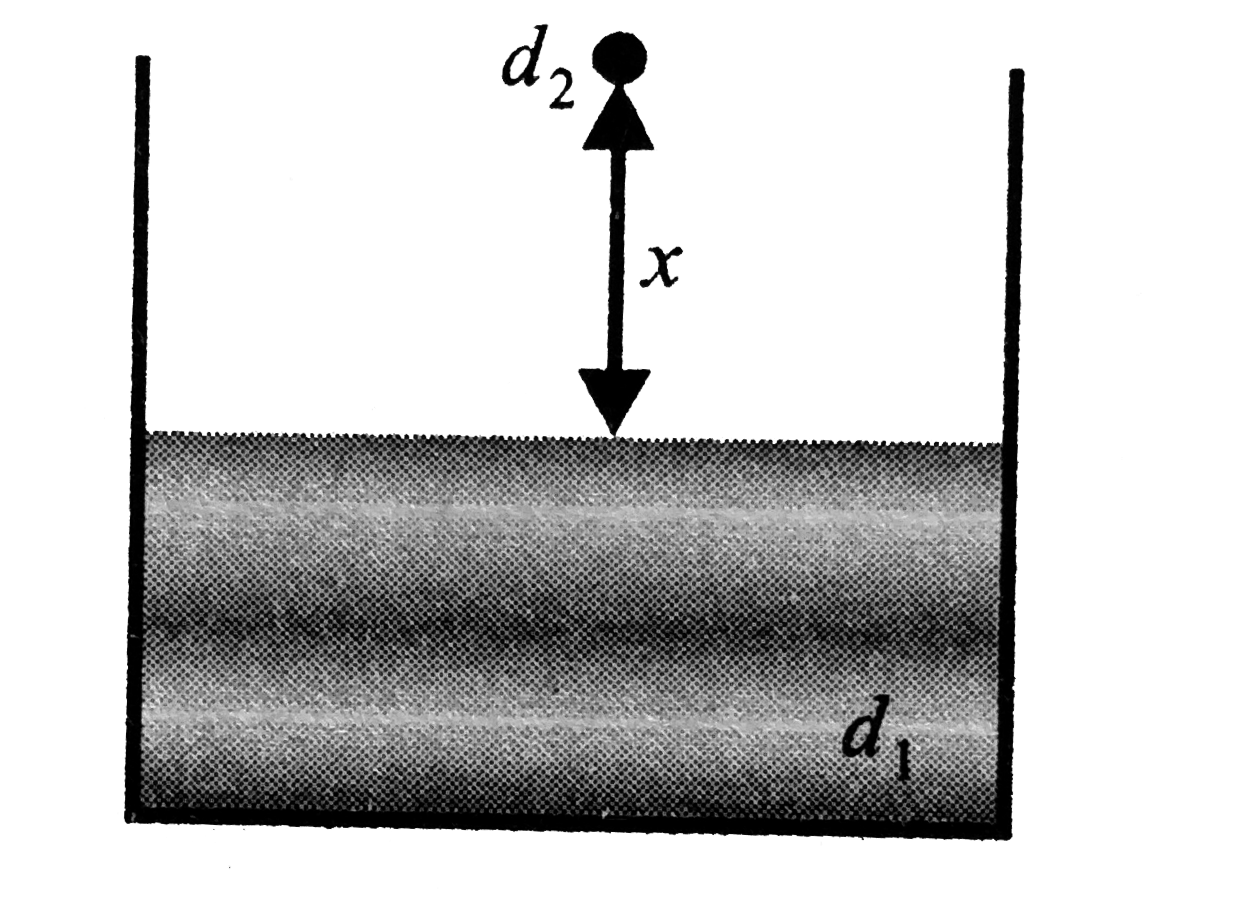
View SolutionA body of density d2 is dropped from rest at a height x into a beaker having a liquid of density d1(d2>d1). Which of the following is/are true?
View Solution
