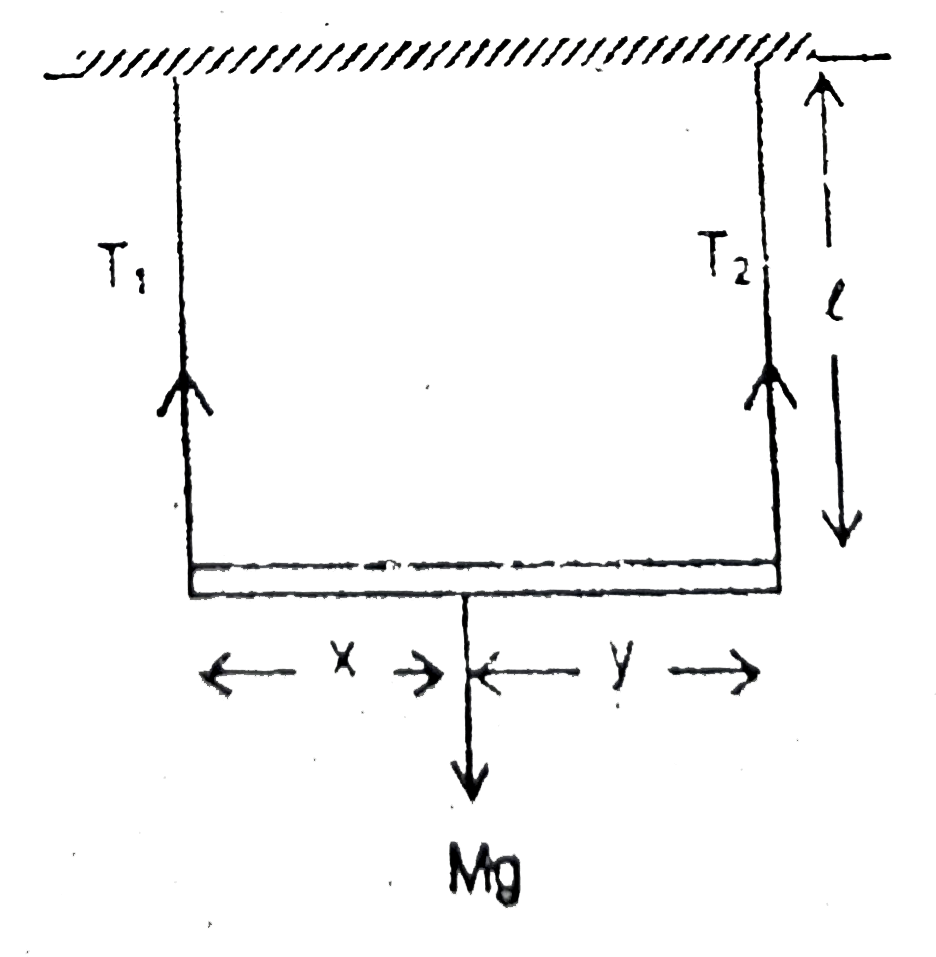
Two strings of the same length but different mass per unit length are used to suspend a rod whose density varies as ρ=ρ0[1+αx] as shown in the figure. The frequency of standing waves produced in the string is in the ratio n:1, when both the strings are vibrating in their fundamental mode. If the mass per unit length of string (l) is μ0, calculate the mass per unit length of the other string.
![Two strings of the same length but different mass per unit length are used to suspend a rod whose density varies as rho=rho(0)[1+alphax] as shown in the figure. The frequency of standing waves produced in the string is in the ratio n : 1, when both the strings are vibrating in their fundamental mode. If the mass per unit length of string (l) is mu(0), calculate the mass per unit length of the other string.](https://d10lpgp6xz60nq.cloudfront.net/physics_images/FIT_JEE_PHY_GMP_ASS_E01_028_Q01.png)
A0e−λt=N0e−λt
& y=L−x=αL2+3L3[αL+2]
T1L=Mgy where M=∫L0aρ0[1+x]dx=aρ0[2L+αL2]2
⇒T1=aρ0gL[3+αL]6, T2=aρ0L[3+2αL]6
V1=√aρ0L[αL+3]6μ0, V2=√aρ0gL[3+2αL]6μ2
Dividing, V1V2=n=f1/f2
μ2=μ0n2[3+2αL]αL+3
Similar Questions
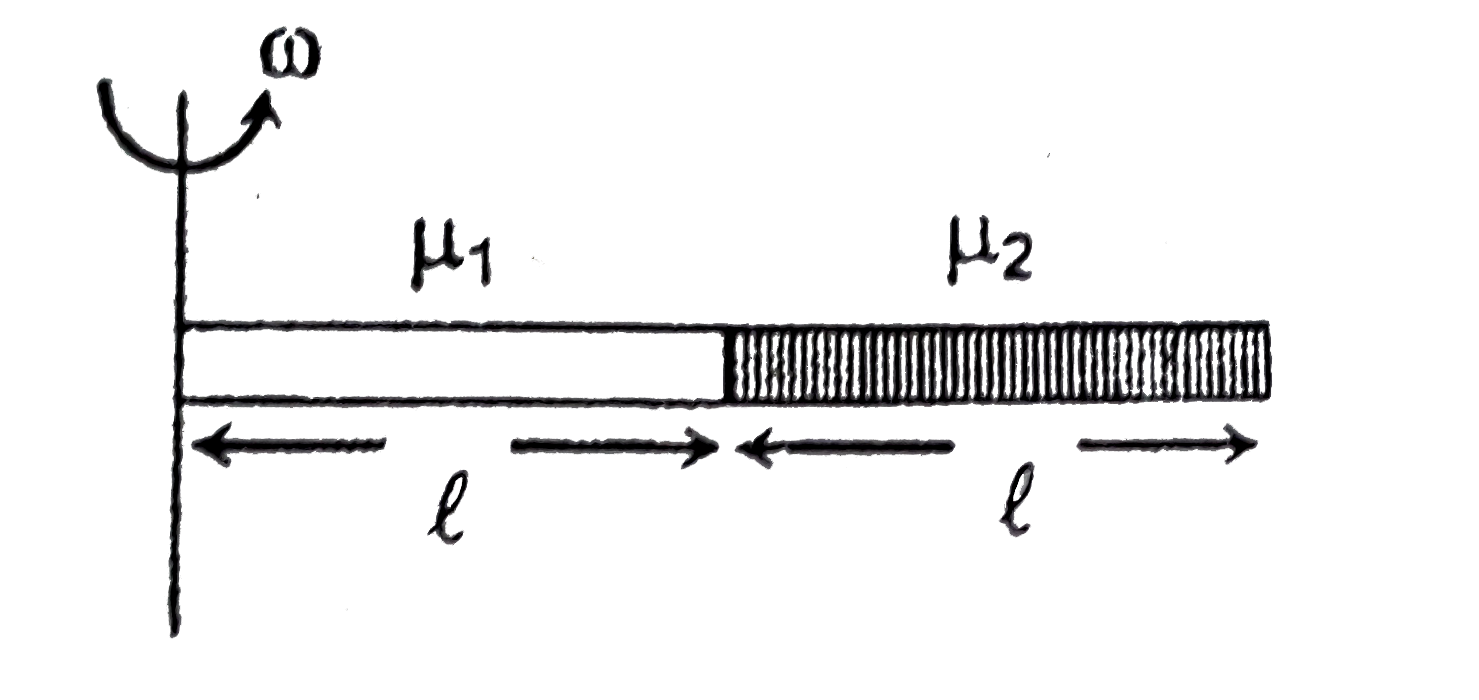
Two thin rods of same length l but of different uniform mass per unit length μ1 and μ2 respectively are joined together. The system is ortated on smooth horizontal plane as shown in figure. The tension at the joint will be
View SolutionA standing wave is produced on a string on a string clamped at one end and free at the other. The length of the string
View SolutionA string tied between x=0andx=l vibrates in fundamental mode. The amplitude A, tension T and mass per unit length μ is given. Find the total energy of the string.

View SolutionDerive an expression for the velocity of pulse in a in stretched in string under a tension T and μ is the mass per unit length of the sting.
View SolutionA string of length and mass per unit length is used in atwood machine as shown in the figure. Masses of blocks are large in comparison with the mass of string. The transverse wave velocity in the string is:
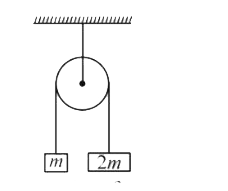
View SolutionA string of length and mass per unit length is used in atwood machine as shown in the figure. Masses of blocks are large in comparison with the mass of string. The transverse wave velocity in the string is:

View SolutionThe frequency (f) of a stretched string depends upen the tension F (dimensions of form ) of the string and the mass per unit length mu of string .Derive the formula for frequency
View SolutionThree strings of equal lengths but stretched with different tensions are inade to vibrate. If their masses per unit length are in the ratio 1:2:3 and the frequencies are the same, calculate the ratio of the tensions.
View SolutionA transverse wave is propagating on a stretched string of mass per unit length32gm−1. The tension on the string is 80 N. The speed of the wave over the string is
View SolutionThe frequency v of the stretched string may depend on (i) the length of the vibrating segment 1 (ii) the tension in the string and (iii) the mass per unit length m. Show that v∝1l√Fm.
View Solution

