The frequency v of the stretched string may depend on (i) the length of the vibrating segment 1 (ii) the tension in the string and (iii) the mass per unit length m. Show that .
To show that the frequency v of a stretched string is proportional to 1L√Fm, we will use dimensional analysis. Here are the steps:
Step 1: Identify the variables
We have three variables that affect the frequency v:
- L: Length of the vibrating segment
- F: Tension in the string
- m: Mass per unit length of the string
Step 2: Express the relationship
We can express the frequency v as a function of these variables:
v=k⋅Lx⋅Fy⋅mz
where k is a dimensionless constant, and x,y,z are the powers to be determined.
Step 3: Write the dimensions of each variable
- The dimension of frequency v is (v)=T−1
- The dimension of length L is (L)=L
- The dimension of force F is (F)=MLT−2
- The dimension of mass per unit length m is (m)=ML−1
Step 4: Substitute dimensions into the equation
Substituting the dimensions into our equation gives:
(T−1)=(L)x⋅(F)y⋅(m)z
This translates to:
T−1=Lx⋅(MLT−2)y⋅(ML−1)z
Step 5: Expand the dimensions
Expanding the right side:
T−1=Lx⋅My⋅Ly⋅T−2y⋅Mz⋅L−z
Combining like terms:
T−1=My+z⋅Lx+y−z⋅T−2y
Step 6: Set up equations for each dimension
Now we can set up equations based on the equality of dimensions:
1. For mass: 0=y+z
2. For length: 0=x+y−z
3. For time: −1=−2y
Step 7: Solve the equations
From the third equation:
−1=−2y⟹y=12
Substituting y into the first equation:
0=12+z⟹z=−12
Now substituting y and z into the second equation:
0=x+12+12⟹x=−1
Step 8: Write the final relationship
Now substituting the values of x,y,z back into the original equation:
v=k⋅L−1⋅F12⋅m−12
This can be rewritten as:
v∝1L√Fm
Conclusion
Thus, we have shown that:
v∝1L√Fm
We have three variables that affect the frequency v:
- L: Length of the vibrating segment
- F: Tension in the string
- m: Mass per unit length of the string
We can express the frequency v as a function of these variables:
v=k⋅Lx⋅Fy⋅mz
where k is a dimensionless constant, and x,y,z are the powers to be determined.
- The dimension of frequency v is (v)=T−1
- The dimension of length L is (L)=L
- The dimension of force F is (F)=MLT−2
- The dimension of mass per unit length m is (m)=ML−1
Substituting the dimensions into our equation gives:
(T−1)=(L)x⋅(F)y⋅(m)z
This translates to:
T−1=Lx⋅(MLT−2)y⋅(ML−1)z
Expanding the right side:
T−1=Lx⋅My⋅Ly⋅T−2y⋅Mz⋅L−z
Combining like terms:
T−1=My+z⋅Lx+y−z⋅T−2y
Now we can set up equations based on the equality of dimensions:
1. For mass: 0=y+z
2. For length: 0=x+y−z
3. For time: −1=−2y
From the third equation:
−1=−2y⟹y=12
0=12+z⟹z=−12
0=x+12+12⟹x=−1
Now substituting the values of x,y,z back into the original equation:
v=k⋅L−1⋅F12⋅m−12
This can be rewritten as:
v∝1L√Fm
Thus, we have shown that:
v∝1L√Fm
Topper's Solved these Questions
- DIMENSIONSBook:ICSEChapter:DIMENSIONSExercise:SHORT ANSWER QUESTIONS WITH ANSWERS
Explore 10 Videos
- DIMENSIONSBook:ICSEChapter:DIMENSIONSExercise:LONG ANSWER QUESTIONS
Explore 3 Videos
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:OBJECTIVE QUESTIONS FROM PREVIOUS IAS EXAMINATIONS
Explore 50 Videos
- DYNAMICSBook:ICSEChapter:DYNAMICSExercise:SHORT ANSWER QUESTIONS WITH ANSWERS
Explore 12 Videos
Similar Questions
The frequency (f) of a stretched string depends upen the tension F (dimensions of form ) of the string and the mass per unit length mu of string .Derive the formula for frequency
View SolutionThe frequency of vibration of string depends on the length L between the nodes, the tension F in the string and its mass per unit length m. Guess the expression for its frequency from dimensional analysis.
View SolutionDerive an expression for the velocity of pulse in a in stretched in string under a tension T and μ is the mass per unit length of the sting.
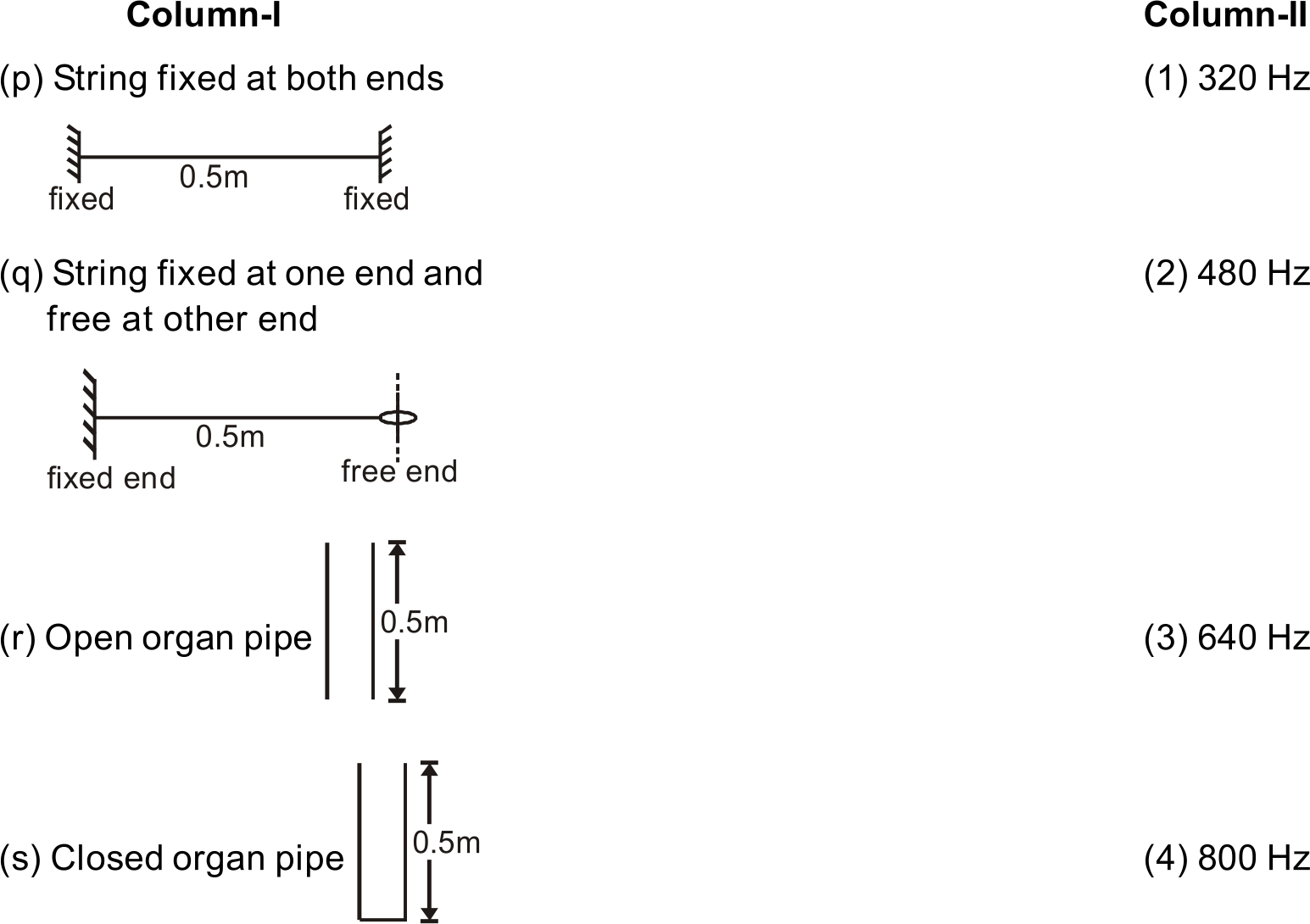
View SolutionIn each of the four situations of column-I , a stretched string or an organ pipe is given along with the required data. In case of strings the tension in string is T=102.4 N and the mass per unit length of string is 1g/m. Speed of sound in air is 320 m/s. Neglect end corrections.The frequencies of resonance are given in column-II.Match each situation in column-I with the possible resonance frequencies given in Column-II.
View SolutionA 5.5 m length of string has a mass of 0.035 kg. If the tension in the string is 77 N the speed of a wave on the string is
View SolutionTwo strings of the same length but different mass per unit length are used to suspend a rod whose density varies as ρ=ρ0[1+αx] as shown in the figure. The frequency of standing waves produced in the string is in the ratio n:1, when both the strings are vibrating in their fundamental mode. If the mass per unit length of string (l) is μ0, calculate the mass per unit length of the other string.
View SolutionThe velocity of transverse wave in a string is v=√T/m where T is the tension in the string and m is the mass per unit length . If T=3.0kgf, the mass of string is 25g and length of the string isv=1.000m, then the percentage error in the measurement of velocity is
View SolutionA transverse wave is propagating on a stretched string of mass per unit length32gm−1. The tension on the string is 80 N. The speed of the wave over the string is
View SolutionA string tied between x=0andx=l vibrates in fundamental mode. The amplitude A, tension T and mass per unit length μ is given. Find the total energy of the string.

View SolutionString-1 is connected with string-2. The mass per unit length in string-1 is μ1 and the mass per unit length in string-2 is 4μ1. The tension in the strings is T. A travelling wave is coming from the left. What fraction of the energy in the incident wave goes into string-2 ?

View Solution