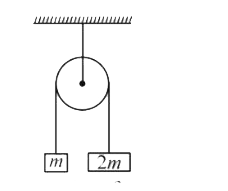
A string of length and mass per unit length is used in atwood machine as shown in the figure. Masses of blocks are large in comparison with the mass of string. The transverse wave velocity in the string is:
√4mgμ
√4mg5μ
√4mg3μ
√4mgμ
The correct Answer is:C
T=2(2m)(m)g2m+m
T=4m2g3m, T=4mg3
v=√Tμ, v=√4mg3μ
Topper's Solved these Questions
- MOCK TEST 12Book:VMC MODULES ENGLISHChapter:MOCK TEST 12Exercise:PHYSICS (SECTION 2)
Explore 5 Videos
- MOCK TEST 11Book:VMC MODULES ENGLISHChapter:MOCK TEST 11Exercise:Physics (Section-2)
Explore 5 Videos
- MOCK TEST 13Book:VMC MODULES ENGLISHChapter:MOCK TEST 13Exercise:PHYSICS ( SECTION -2)
Explore 5 Videos
Similar Questions
Consider the double Atwood's machine as shown in the figure
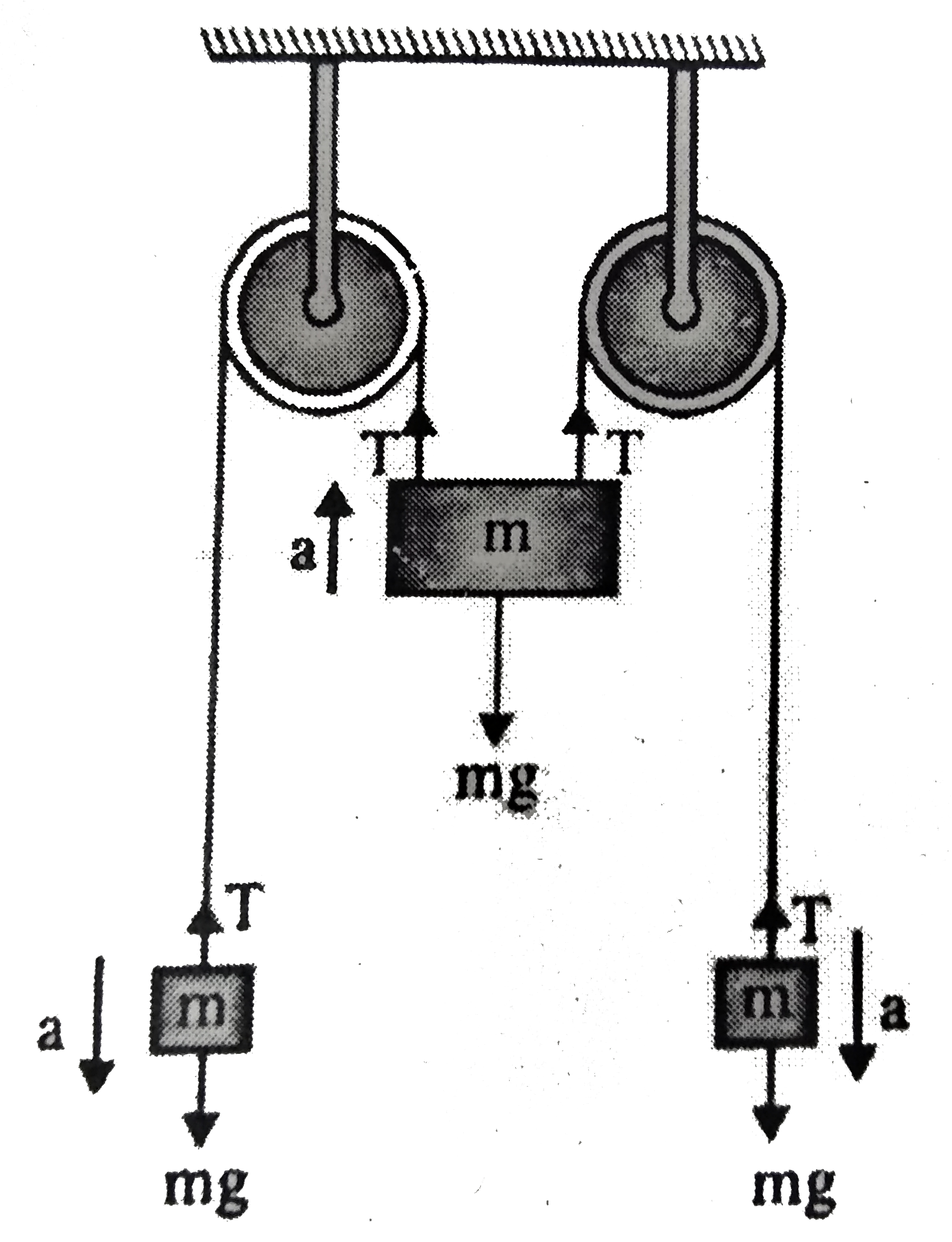
(a) What is acceleration of the masses?
(b) What is the tension in each string?
View SolutionTwo block each of mass 'm' are attached with two elastic strings as shown in the figure. Masses of strings are negligible in comparison to block of mass 'm' density of material of each string is ρ. The whole system is moving vertically upward with an acceleration a = g/2. It is in equilibrium with respect to elevator.
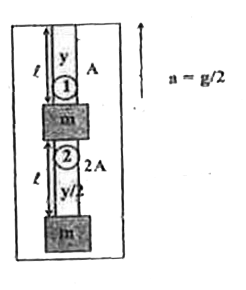
Ratio of elongation in rod 1 to that of rod 2 will be
View SolutionTwo block each of mass 'm' are attached with two elastic strings as shown in the figure. Masses of strings are negligible in comparison to block of mass 'm' density of material of each string is ρ. The whole system is moving vertically upward with an acceleration a = g/2. It is in equilibrium with respect to elevator.
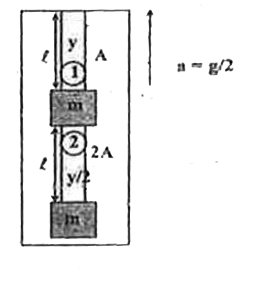
Ratio of PE stored in string-1 to string-2 in equilibrium is
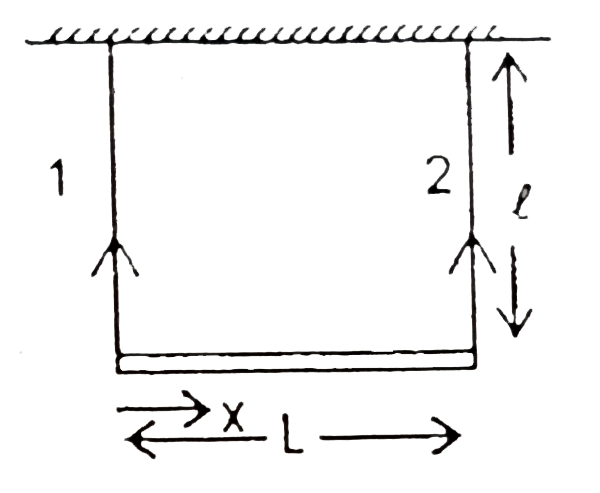
View SolutionTwo strings of the same length but different mass per unit length are used to suspend a rod whose density varies as ρ=ρ0[1+αx] as shown in the figure. The frequency of standing waves produced in the string is in the ratio n:1, when both the strings are vibrating in their fundamental mode. If the mass per unit length of string (l) is μ0, calculate the mass per unit length of the other string.
View SolutionConsider the double Atwood's machine as shown in the figure
(a) Whatis acceleration of the masses?
(b) What is the tension in each string?

View SolutionThe block of mass m is at rest. Find the tension in the string A .

View SolutionA uniform rod of length l and mass m is hung from, strings of equal length from a ceiling as shown in figure. Determine the tensions in the strings?

View SolutionA block of mass m is tied to a string of length L and the assembly is kept on a smooth horizontal table as shown in the figure. Now the other end of the string is moved with a constant velocity v0ˆj. (xy plane is the plane of the table) Then

View SolutionString-1 is connected with string-2. The mass per unit length in string-1 is μ1 and the mass per unit length in string-2 is 4μ1. The tension in the strings is T. A travelling wave is coming from the left. What fraction of the energy in the incident wave goes into string-2 ?

View SolutionTwo strings A and B are connected together end to end as shown in the figure. The ratio of mass per unit length μBμA=4. The tension in the string is same. A travelling wave is coming from the string A towards string B. if the fraction of the power of the incident wave that goes in sting B is n9 the value of n is:

View Solution