String-1 is connected with string-2 The mass per unit length in string-1 is μ1 and mass per unit length in string-2 is 4μ1. The tension in the strings is T .A travelling wave is coming from the left .What fraction of the energy in the incident wave goes into string-2?
18
49
23
89
The correct Answer is:A
To solve the problem of finding the fraction of energy in the incident wave that goes into string-2, we will follow these steps:
Step 1: Understand the Energy of the Wave
The energy of a wave traveling in a string can be expressed as:
E=12μω2A2v
where:
- μ = mass per unit length of the string,
- ω = angular frequency of the wave,
- A = amplitude of the wave,
- v = velocity of the wave in the string.
Step 2: Calculate the Energy in String-1
For string-1, with mass per unit length μ1:
E1=12μ1ω2A2v1
Step 3: Determine the Velocity in String-1
The velocity of the wave in string-1 is given by:
v1=√Tμ1
where T is the tension in the string.
Step 4: Calculate the Energy in String-2
For string-2, with mass per unit length μ2=4μ1:
E2=12μ2ω2A2tv2
where At is the transmitted amplitude and v2 is the velocity in string-2.
Step 5: Calculate the Velocity in String-2
The velocity of the wave in string-2 is:
v2=√Tμ2=√T4μ1=12√Tμ1=v12
Step 6: Calculate the Transmitted Amplitude
The transmitted amplitude At can be calculated using the formula:
At=A⋅2√μ1√μ1+√4μ1=A⋅2√μ1√μ1+2√μ1=A⋅23
Step 7: Substitute Values into Energy Equation for String-2
Now substitute At and v2 into the energy equation for string-2:
E2=12(4μ1)ω2(2A3)2(v12)
E2=12(4μ1)ω2(4A29)(v12)
E2=4μ1ω2A2v19
Step 8: Calculate the Fraction of Energy Transmitted
Now we need to find the fraction of energy transmitted:
Fraction=E2E1
Substituting E1 and E2:
Fraction=4μ1ω2A2v1912μ1ω2A2v1
Fraction=4/91/2=49⋅2=89
Final Answer
The fraction of the energy in the incident wave that goes into string-2 is:
89
The energy of a wave traveling in a string can be expressed as:
E=12μω2A2v
where:
- μ = mass per unit length of the string,
- ω = angular frequency of the wave,
- A = amplitude of the wave,
- v = velocity of the wave in the string.
For string-1, with mass per unit length μ1:
E1=12μ1ω2A2v1
The velocity of the wave in string-1 is given by:
v1=√Tμ1
where T is the tension in the string.
For string-2, with mass per unit length μ2=4μ1:
E2=12μ2ω2A2tv2
where At is the transmitted amplitude and v2 is the velocity in string-2.
The velocity of the wave in string-2 is:
v2=√Tμ2=√T4μ1=12√Tμ1=v12
The transmitted amplitude At can be calculated using the formula:
At=A⋅2√μ1√μ1+√4μ1=A⋅2√μ1√μ1+2√μ1=A⋅23
Now substitute At and v2 into the energy equation for string-2:
E2=12(4μ1)ω2(2A3)2(v12)
E2=12(4μ1)ω2(4A29)(v12)
E2=4μ1ω2A2v19
Now we need to find the fraction of energy transmitted:
Fraction=E2E1
Substituting E1 and E2:
Fraction=4μ1ω2A2v1912μ1ω2A2v1
Fraction=4/91/2=49⋅2=89
The fraction of the energy in the incident wave that goes into string-2 is:
89
Topper's Solved these Questions
- WAVE MOTION Book:TARGET PUBLICATIONChapter:WAVE MOTION Exercise:MCQ 7.1
Explore 61 Videos
- SURFACE TENSION Book:TARGET PUBLICATIONChapter:SURFACE TENSION Exercise:EVALUATION TEST
Explore 21 Videos
- WAVE THEORY OF LIGHT Book:TARGET PUBLICATIONChapter:WAVE THEORY OF LIGHT Exercise:EVALUATION TEST
Explore 20 Videos
Similar Questions
Two strings A and B are connected together end to end as shown in the figure. The ratio of mass per unit length μBμA=4. The tension in the string is same. A travelling wave is coming from the string A towards string B. if the fraction of the power of the incident wave that goes in sting B is n9 the value of n is:

View SolutionIf T is the tension in the sting μ is the linear density of the string,then the velocity of transverse wave in the string
View Solution
Knowledge Check
A string consists of two parts attached at x=0 , The right part of the string (x<0) has mass per unit length μr and the left part of the string (x<0) has mass per unit length μl The tension in the string is T. If a wave of units amplitude travels along the left part of the string,what is the amplitude of the wave that is transmitted to the right part of the string?
A1B21+√μl/μyC21+√μl/μyD√μl/μy−1√μl/μy+1A string of mass per unit length 0.2 kg m−1 and length 0.6 m is fixed at both ends such that it has a tension of 80 N. If the string is vibrating in its second overtone mode, then the frequency of the string is
A40 HzB50 HzC60 HzD70 HzA 5.5 m length of string has a mass of 0.035 kg. If the rension in the string is 77 N the speed of a wave on the string is
A110ms−1B165ms−1C77ms−1D102ms−1
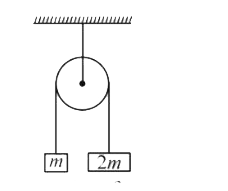
A string of length and mass per unit length is used in atwood machine as shown in the figure. Masses of blocks are large in comparison with the mass of string. The transverse wave velocity in the string is:
View SolutionA transverse wave is propagating on a stretched string of mass per unit length32gm−1. The tension on the string is 80 N. The speed of the wave over the string is
View SolutionA 5.5 m length of string has a mass of 0.035 kg. If the tension in the string is 77 N the speed of a wave on the string is
View SolutionA long string is constructed by joining the ends of two shorter strings. The tension in the strings is the same but string I has 4 times the linear mass density of string II. When a sinusoidal wave passes from string I to string II:
View SolutionA 5.5 m length of string has a mass of 0.035 kg. If the tension in the string is 77 N the speed of a wave on the string is
View Solution

