For the arrangement shown, a cylinder of mass m with cross-sectional area A, initially in equilibrium poisition, is displaced slightly inside the liquid of density p. Prove that the motion is simple harmonic and also find its time-period.
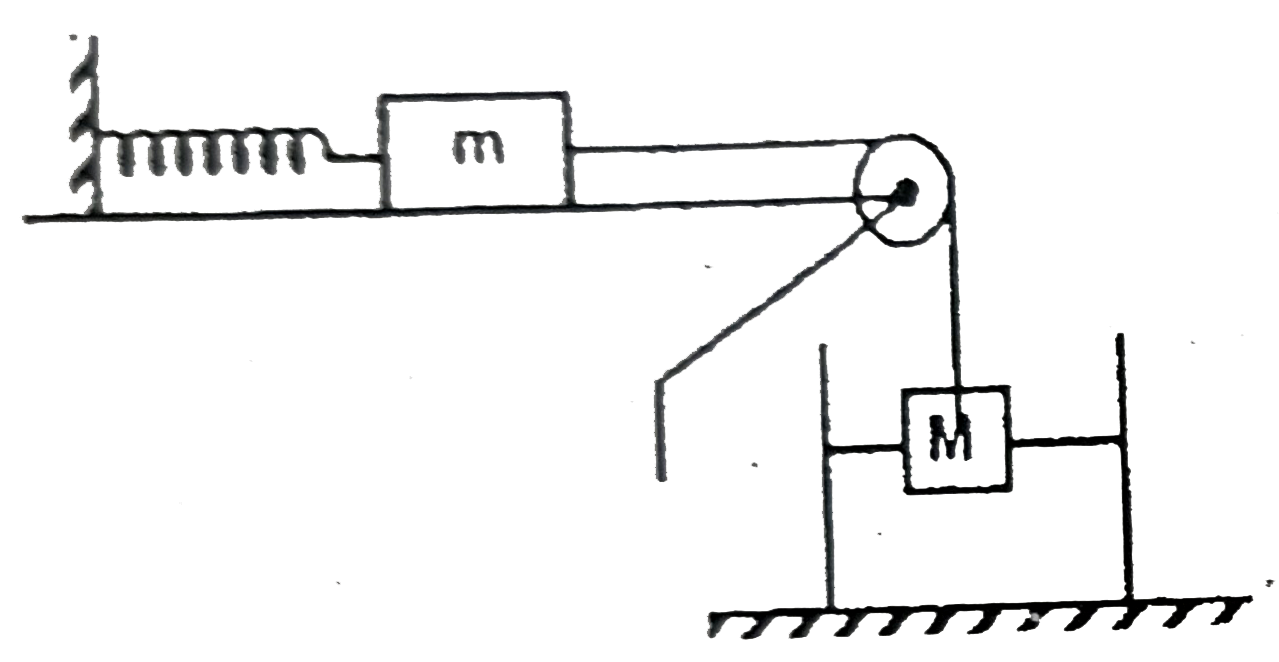
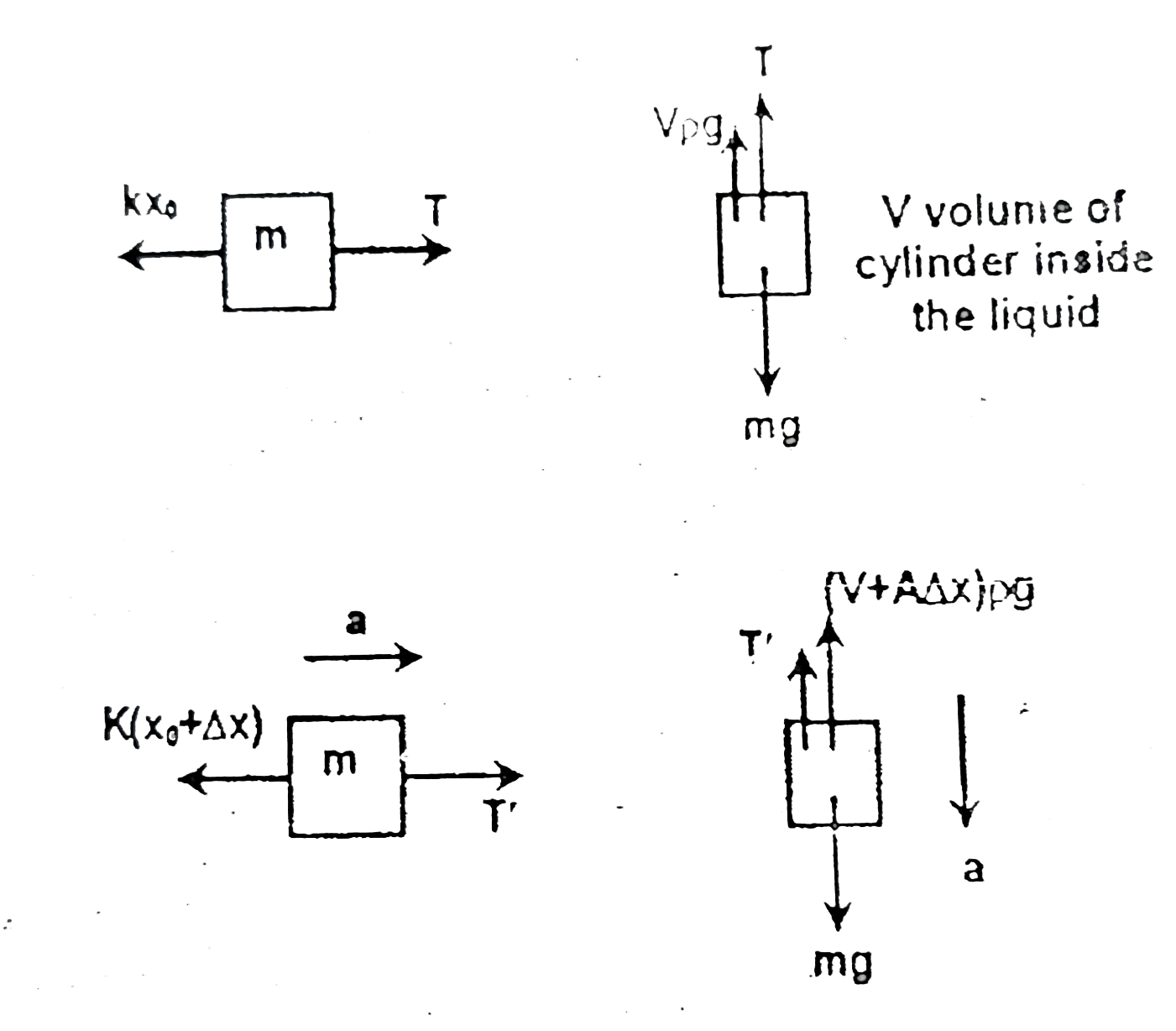
T=kx0
and T+Vρg=mg
⇒kx0+Vρg=mg
when m is displaced by Δx downwards
ma=T'−k(x0+Δx)
⇒ma=mg−(v+Aδx)ρg−T'
Adding 2ma=mg−k(x0+Δx)−(v+AΔx)ρg
=−[k+Aρg]Δx, using equation (3)
⇒a=−[k+Aρg]2mΔx
∴T=2πω=2π√2m[k+Aρg]
Similar Questions
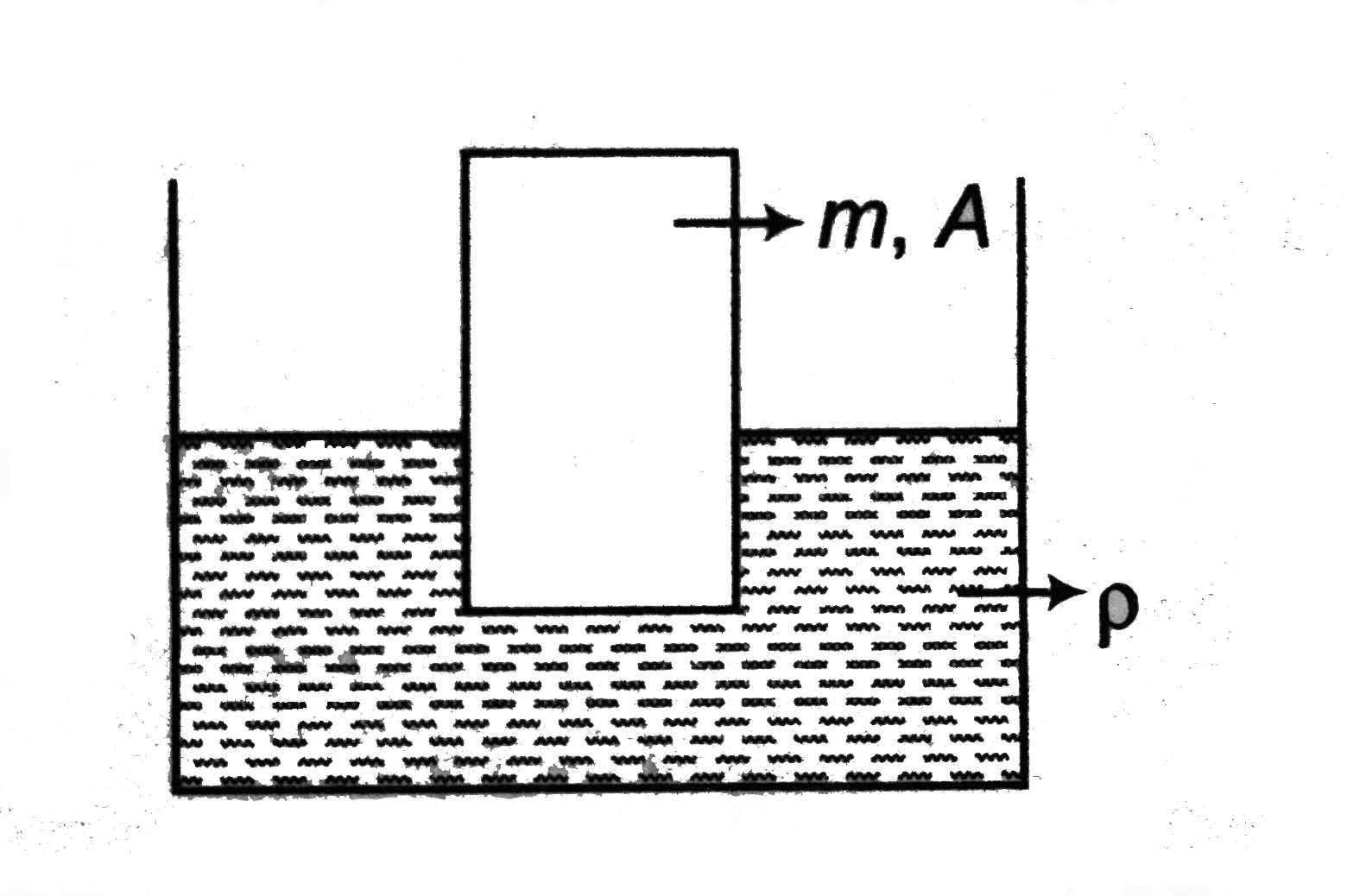
A plank of mass 'm' and area of cross - section A is floating in a non - viscous liquid of desity ρ. When displaced slightly from the mean position, it starts oscillating. Prove that oscillations are simple harmonic and find its time period.
View SolutionA charged particle q of mass m is in wquilibrium at a height h from a horizontal infinite line charge wit uniform linear charge density λ. The charge lies in the vertical plane containing the line charge. If the particle is displaced slightly (vertically) prove that the motion of the charged particle will be simple harmonic. Also find its time period.
View SolutionConsider the situastion shown in figure. Show that if that blocks are displaced slightly in opposite directions and released, they will execute simple harmonic motion. Calculate the time period.
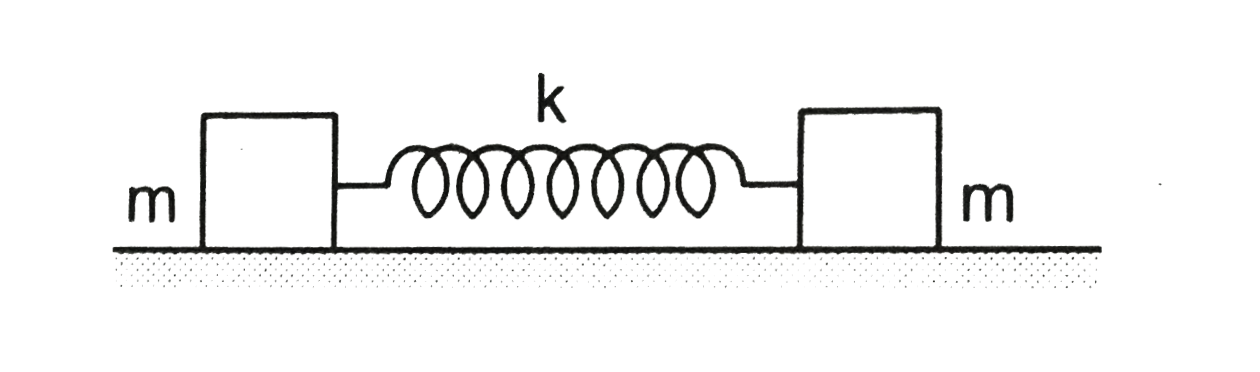
View SolutionConsider the situation shown in figure. Show that if the blocks are displaced slightly in opposite directions and released, they will execute simple harmonic motion. Calculate the time period.

View SolutionA body of mass m is suspended from three springs as shown in figure. If mass m is displaced slightly then time period of oscillation is

View SolutionA thin rod of length L and area of cross section S is pivoted at its lowest point P inside a stationary, homogeneous and non-viscous liquid. The rod is free to rotate in a vertical plane about a horizontal axis passing through P. The density d1of the rod is smaller than the density d2 of the liquid. The rod is displaced by a small angle theta from its equilibrium position and then released. Shown that the motion of the rod is simple harmonic and determine its angular frequency in terms of the given parameters ___________ .
View SolutionA vertical U tube contains a liquid of density ρ, length of the liquid in the tube is 2H. The liquid is displaced slightly and released. Show that the liquid will execute SHM. Also find its time period. Take liquid to be ideal.

View SolutionIs oscillation of a mass suspended by a spring simple harmonic ? give expression for its time period also.
View SolutionA ball of mass m kept at the centre of a string of length L is pulled from centre in perpendicular direction and released. Prove that motion of ball is simple harmonic and determine time period of oscillation
View SolutionA vertical pole of length l , density ρ , area of cross section A floats in two immiscible liquids of densities ρ1and ρ2. In equuilibrium possition the bottom end is at the interface of the liquids. When the cylinder is displaced vertically, find the time period of oscillation.
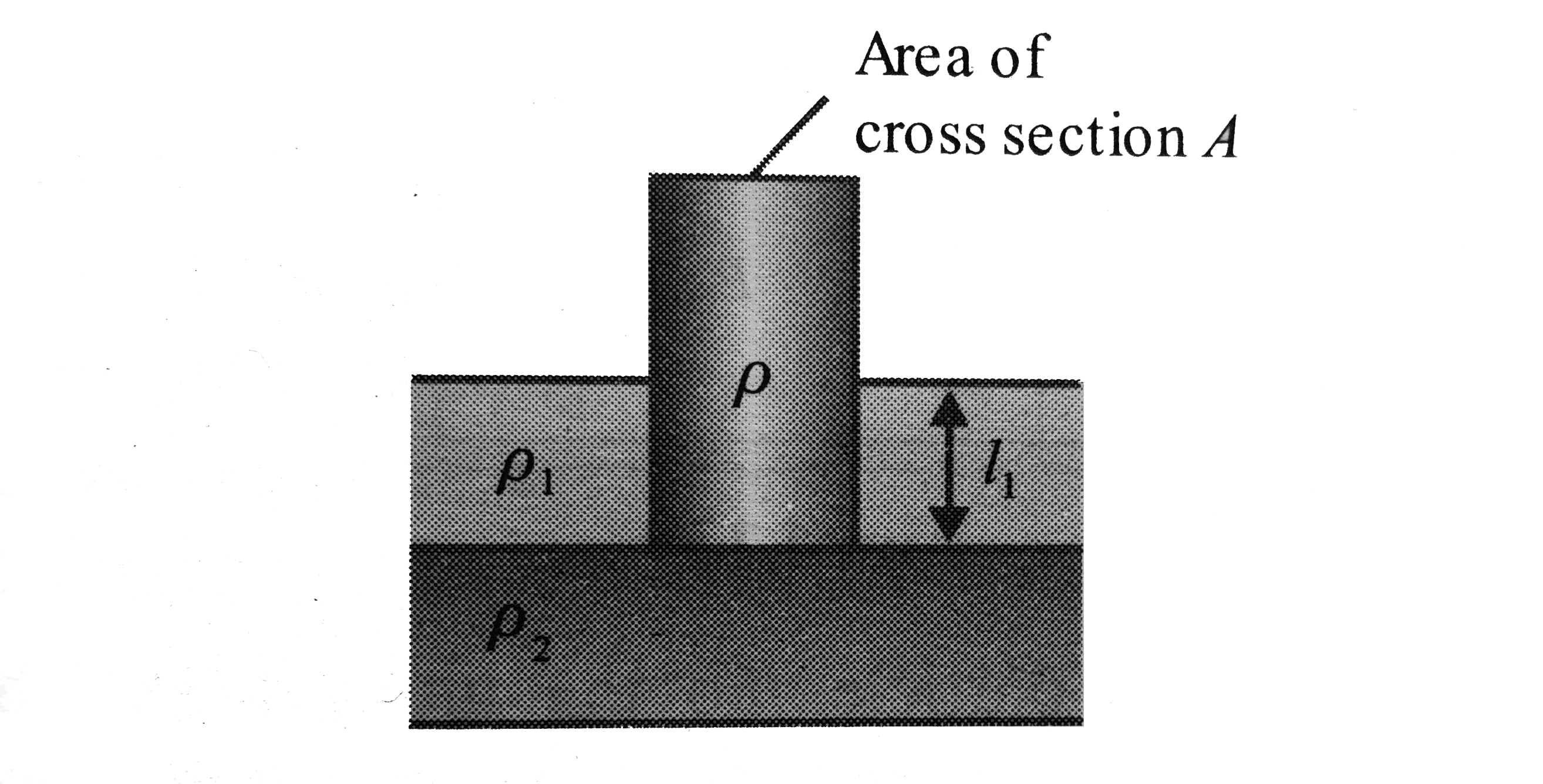
View Solution