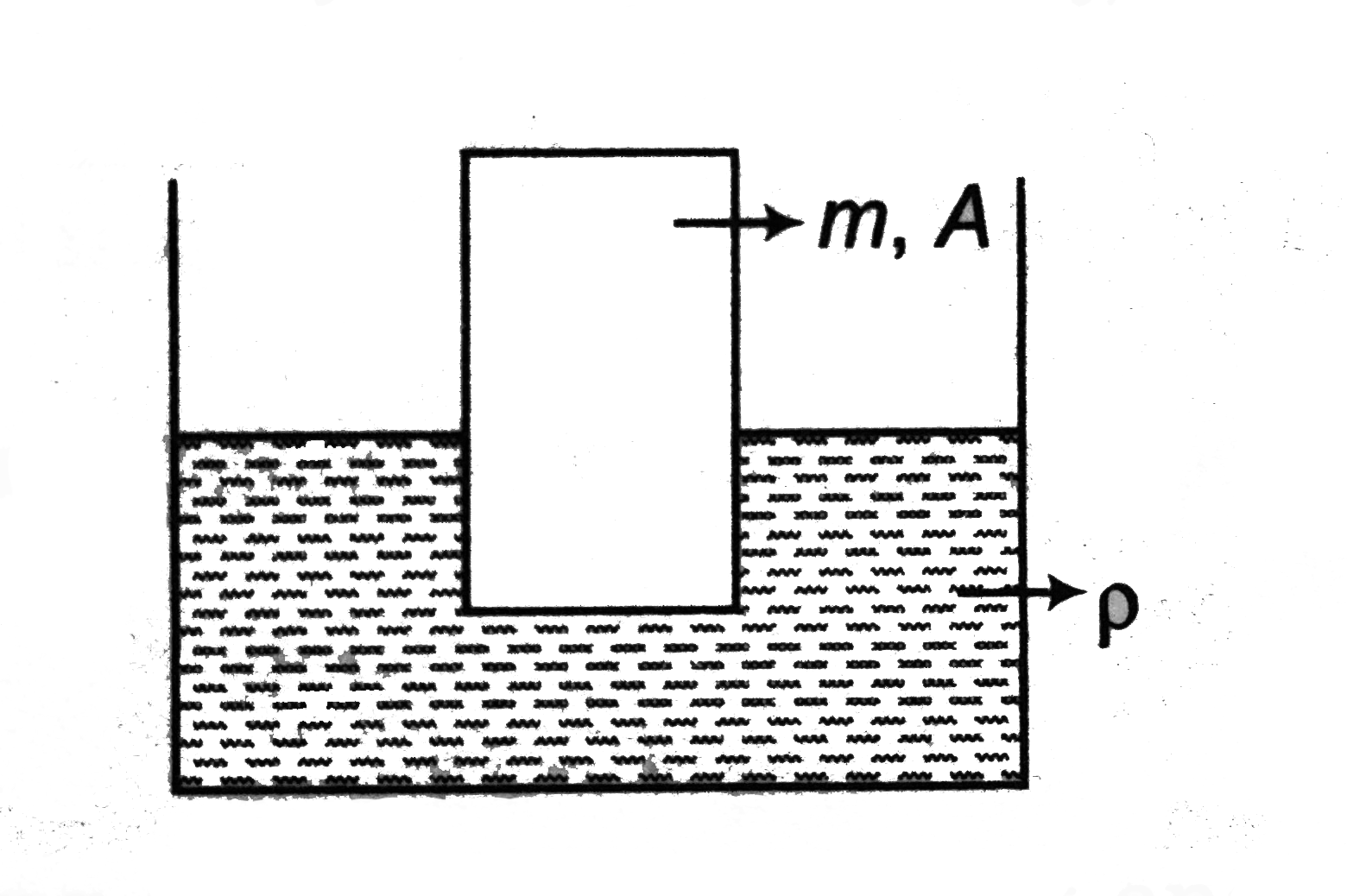
A piece of wood of mass m is floating erect in a liquid whose density is ρ . If it is slightly pressed down and released, then executes simple harmonic motion. Show that its time period of oscillation is T=2π√mAρg Solution in Tamil
Spring factor of liquid = Aρg
Inertia factor of wood piece = m
Time period T=2π√Inertia factorSpring factor
T=2π√mAρg
Topper's Solved these Questions
- OSCILLATIONSBook:SURA PUBLICATIONChapter:OSCILLATIONSExercise:ADDITIONAL QUESTIONS (I MULTIPLE CHOICE QUESTIONS)
Explore 20 Videos
- OSCILLATIONSBook:SURA PUBLICATIONChapter:OSCILLATIONSExercise:ADDITIONAL QUESTIONS (III. FILL IN THE BLANKS)
Explore 10 Videos
- OSCILLATIONSBook:SURA PUBLICATIONChapter:OSCILLATIONSExercise:EXERCISE QUESTIONS (III. LONG ANSWER QUESTIONS)
Explore 10 Videos
- NATURE OF PHYSICAL WORLD AND MEASUREMENTBook:SURA PUBLICATIONChapter:NATURE OF PHYSICAL WORLD AND MEASUREMENTExercise:ADDITIONAL QUESTIONS
Explore 241 Videos
- PROPERTIES OF MATTERBook:SURA PUBLICATIONChapter:PROPERTIES OF MATTERExercise:Value based Questions
Explore 5 Videos
Similar Questions
A Particle excites simple harmonic motion between x=−A&x=+A , the time taken for it to go from O to A2 is T1 & to go from A2 to A is T2 then
View SolutionThe time period for U - tube Oscillation is ……….. .
View SolutionWhat is meant by simple harmonic oscillation ? Give example
View SolutionA substance whose mas is 4.27 g occupies 1.3cm3. The number of significant figure in density is
View Solutionthe r.m.s. velocity of the molecules of a certain diatomic gas is found to be 1.6 Km/sec. the gas is
View SolutionA plank of mass 'm' and area of cross - section A is floating in a non - viscous liquid of desity ρ. When displaced slightly from the mean position, it starts oscillating. Prove that oscillations are simple harmonic and find its time period.
View SolutionA cylinderical log of wood of height h and area of cross-section A floats in water. It is pressed and then released. Show that the log would execute S.H.M. with a tiem period. T=2pisqrt((m)/(Arhog) where m is mass of the body and rho is density of the liquid.
View SolutionA cylidrical wooden piece of cork floats in a liquid of density σ. The cork is depressed slightly and released. Show that the cork will oscillate up and down simple harmonicaly with a period.
T=2π√ρhσg, where ρ is the density of the cork.
View SolutionA cylindrical piece of cork of density rho , base area A and height h, floats in a liquid of density rho_(1) . The cork is depressed slightly and then released. Show that the cork oscillates up and down simple harmonically, with a period T=2pisqrt((hrho)/(rho_(1)g)) , where 'rho' is the density of the cork.
View SolutionA piece of wood of mass m is floating erect in a liquid whose density is ρ . If it is slightly pressed down and released, then executes simple harmonic motion. Show that its time period of oscillation is T=2π√mAρg
View SolutionA piece of wood of mass m is floating erect in a liquid whose density is ρ . If it is slightly pressed down and released, then executes simple harmonic motion. Show that its time period of oscillation is T=2π√mAρg
View SolutionA piece of wood of mass m is floating erect in a liquid whose density is ρ . If it is slightly pressed down and released, then executes simple harmonic motion. Show that its time period of oscillation is T=2π√mAρg
View SolutionA cylindrical piece of cork of density of base area A and height h floats in a liquid of density p1. The cork is depressed slightly and then released. Show that the cork oscillates up and down simple harmonically with a period
T=2π√hpp1g
where p is the density of cork. (Ignore damping due to viscosity of the liquid).
View SolutionA cylindrical piece of cork of density of base area A and height h floats in a liquid of density pl. The cork is depressed slightly and then released. Show that the cork oscillates up and down simple harmonically with a period
T=2π√hpp1g
where p is the density of cork. (Ignore damping due to viscosity of the liquid).
View SolutionA cylindrical piece of cork of density of base area A and height h floats in a liquid of density ρ1. The cork is depressed slightly and then released. The cork oscillates up and down simple harmonically with period is (ρ is the density of cork)
View Solution

