A piece of wood of mass m is floating erect in a liquid whose density is ρ . If it is slightly pressed down and released, then executes simple harmonic motion. Show that its time period of oscillation is T=2π√mAρg Solution in Tamil
When a wood is pressed and released,
Change in
force (F=ma)
=(Ax)ρg
A=Fm=(Aρg)xm ...(1)
since a=−ω2x ....(2)
From (1) & (2)
ω2=Aρgm
ω=√Aρgm
We know that,
Time period T=2πω=2π√mAρg
Topper's Solved these Questions
- OSCILLATIONS BOOK - PREMIERS PUBLISHERSCHAPTER - OSCILLATIONS EXERCISE - OTHER IMPORTANT QUESTIONS & ANSWERS ( MULTIPLE CHOICE QUESTIONS )
64 Videos
- OSCILLATIONS BOOK - PREMIERS PUBLISHERSCHAPTER - OSCILLATIONS EXERCISE - OTHER IMPORTANT QUESTIONS & ANSWERS ( VERY SHORT ANSWER QUESTIONS )
28 Videos
- OSCILLATIONS BOOK - PREMIERS PUBLISHERSCHAPTER - OSCILLATIONS EXERCISE - EVALUATION TEXTBOOK QUESTIONS AND ANSWERS ( LONG ANSWWERS QUESTIONS :)
20 Videos
- NATURE OF PHYSICAL WORLD AND MEASUREMENTBOOK - PREMIERS PUBLISHERSCHAPTER - NATURE OF PHYSICAL WORLD AND MEASUREMENTEXERCISE - OTHER IMPORTANT QUESTIONS & ANSWERS (III. Short Answer Questions.)
24 Videos
- PROPERTIES OF MATTERBOOK - PREMIERS PUBLISHERSCHAPTER - PROPERTIES OF MATTEREXERCISE - OTHER IMPORTANT QUESTION & ANSWERS (NUMERICAL PROBLEMS)
56 Videos
Similar Questions
Assertion : In simple harmonic motion the velocity is maximum when the acceleration is minimum.
Reason : In simple harmonic motion the phase difference between velocity and acceleration is π2
Select the correct option form the following.
View SolutionState the values of amplitude and frequency of a particle having the equation of simple harmonic motion as.
View SolutionWhat is meant by simple harmonic oscillation ? Give example
View SolutionWhat is meant by Parallax?
View SolutionA material breaks up under a stress of 20×105N/m2. If the density of the material is 2.5×103kg/m3, calculate the length may break under its own weight.(Take g=10m/s2)
View SolutionA plank of mass 'm' and area of cross - section A is floating in a non - viscous liquid of desity ρ. When displaced slightly from the mean position, it starts oscillating. Prove that oscillations are simple harmonic and find its time period.
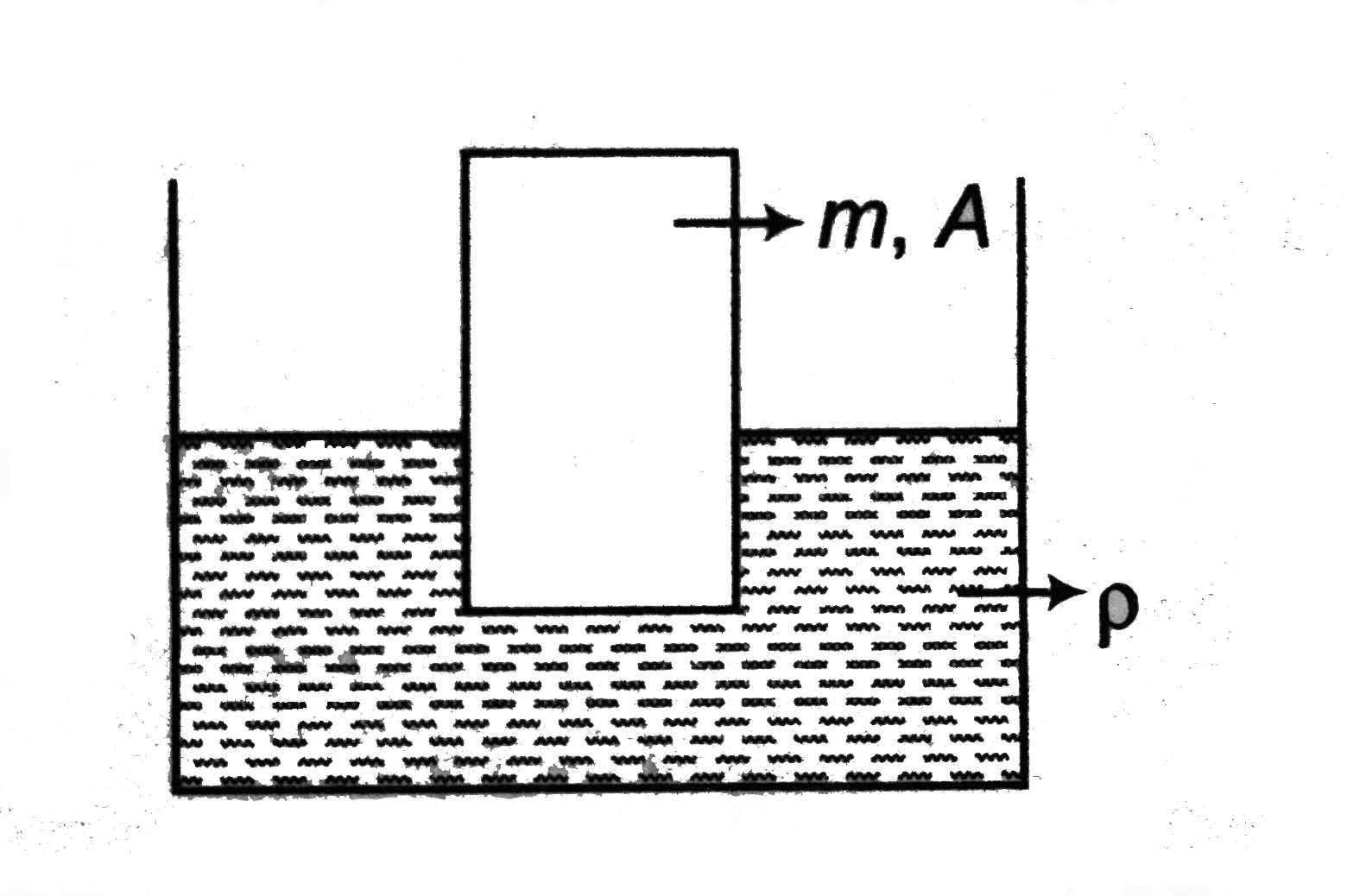
View SolutionA cylinderical log of wood of height h and area of cross-section A floats in water. It is pressed and then released. Show that the log would execute S.H.M. with a tiem period. T=2pisqrt((m)/(Arhog) where m is mass of the body and rho is density of the liquid.
View SolutionA cylidrical wooden piece of cork floats in a liquid of density σ. The cork is depressed slightly and released. Show that the cork will oscillate up and down simple harmonicaly with a period.
T=2π√ρhσg, where ρ is the density of the cork.
View SolutionA piece of wood of mass m is floating erect in a liquid whose density is ρ . If it is slightly pressed down and released, then executes simple harmonic motion. Show that its time period of oscillation is T=2π√mAρg
View SolutionA cylindrical piece of cork of density rho , base area A and height h, floats in a liquid of density rho_(1) . The cork is depressed slightly and then released. Show that the cork oscillates up and down simple harmonically, with a period T=2pisqrt((hrho)/(rho_(1)g)) , where 'rho' is the density of the cork.
View SolutionA piece of wood of mass m is floating erect in a liquid whose density is ρ . If it is slightly pressed down and released, then executes simple harmonic motion. Show that its time period of oscillation is T=2π√mAρg
View SolutionA piece of wood of mass m is floating erect in a liquid whose density is ρ . If it is slightly pressed down and released, then executes simple harmonic motion. Show that its time period of oscillation is T=2π√mAρg
View SolutionA cylindrical piece of cork of density of base area A and height h floats in a liquid of density p1. The cork is depressed slightly and then released. Show that the cork oscillates up and down simple harmonically with a period
T=2π√hpp1g
where p is the density of cork. (Ignore damping due to viscosity of the liquid).
View SolutionA cylindrical piece of cork of density of base area A and height h floats in a liquid of density pl. The cork is depressed slightly and then released. Show that the cork oscillates up and down simple harmonically with a period
T=2π√hpp1g
where p is the density of cork. (Ignore damping due to viscosity of the liquid).
View SolutionA cylindrical piece of cork of density of base area A and height h floats in a liquid of density ρ1. The cork is depressed slightly and then released. The cork oscillates up and down simple harmonically with period is (ρ is the density of cork)
View Solution
