A cylindrical piece of cork of density of base area A and height h floats in a liquid of density p1. The cork is depressed slightly and then released. Show that the cork oscillates up and down simple harmonically with a period
T=2π√hpp1g
where p is the density of cork. (Ignore damping due to viscosity of the liquid).Solution in Bengali
In equilibrium, weight of the cork equals the up thrust. When the cork is depressed by an amount x, the net upward force is Axp1g. Thus the force constant k=Ap1g. Using m = Ahp, and T=2π√mk one gets the given expression.
Topper's Solved these Questions
- OSCILLATIONSBOOK - NCERT BANGLISHCHAPTER - OSCILLATIONSEXERCISE - Additional Exercises
6 Videos
- OSCILLATIONSBOOK - NCERT BANGLISHCHAPTER - OSCILLATIONSEXERCISE - Additional Exercises
6 Videos
- MOTION IN A STRAIGHT LINEBOOK - NCERT BANGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ADDITIONAL EXERCISES
5 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - NCERT BANGLISHCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - EXERCISES (TRUE OR FALSE)
3 Videos
Similar Questions
An air chamber of volume V has a neck area of cross section a into which a ball of mass m just fits and can move up and down without any friction (Fig.14.27). Show that when the ball is pressed down a little and released , it executes SHM. Obtain an expression for the time period of oscillations assuming pressure-volume variations of air to be isothermal [see Fig. 14.27].
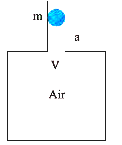
View SolutionAn air chamber of volume V has a neck area of cross section a into which a ball of mass m just fits and can move up and down without any friction (Fig.14.27). Show that when the ball is pressed down a little and released , it executes SHM. Obtain an expression for the time period of oscillations assuming pressure-volume variations of air to be isothermal [see Fig. 14.27].

View SolutionA boy standing on a stationary lift (open from above) throws a ball upwards with the maximum initial speed he can, equal to 49ms−1. How much time does the ball take to return to his hands ? If the lift starts moving up with a uniform speed of 5ms−1 and the boy again throws the ball up with the maximum speed he can, how long does the ball take to return to his hands ?
View SolutionThe instantaneous speed of the point of contact during rolling is zero.
View SolutionA cylindrical piece of cork of base area A and height h floats in a liquid of density rho_(1) . The cork is depressed slightly and then released. Show that the cork oscillates up and down simple harmonically with a period T=2pisqrt((hrho)/(rho_(1)g))
View SolutionA cylidrical wooden piece of cork floats in a liquid of density σ. The cork is depressed slightly and released. Show that the cork will oscillate up and down simple harmonicaly with a period.
T=2π√ρhσg, where ρ is the density of the cork.
View Solutionआधार क्षेत्रफल A तथा ऊँचाई h के एक कॉर्क का बेलनकार दुकड़ा pt घनत्व के किसी द्रव में तैर रहा है | कॉर्क को थोड़ा निचे दबाकर स्वतंत्र छोड़ देते है, यह दर्शाइए कि कॉर्क ऊपर-निचे सरल आवर्त दोलन करता है जिसका आवर्तकाल
T=2π√hpp1g है |
यहाँ p कॉर्क का घनत्व है (द्रव की श्यानता के कारण अवमंदन को नगण्य मानिए ) |
View Solutionआधार क्षेत्रफल A तथा ऊंचाई के h एक कॉर्क का बेलनाकार टुकड़ा pl घनत्व के किसी द्रव में तैर रहा है । कॉर्क को थोड़ा नीचे दबाकर स्वतंत्र छोड़ देते है , यह दर्शाइये कि कॉर्क ऊपर - नीचे सरल आवर्त दोलन करता है जिसका आवर्तकाल T=2π√hpplg है ।
यहाँ ρ कॉर्क का घनत्व है ( द्रव कि श्यानता के कारण अवमन्दन को नगण्य मानिए ।)
View Solutionआधार क्षेत्रफलA तथा ऊँचाई h के कॉर्क का बेलनाकार टुकड़ा ρ1 घनत्व के किसी द्रव पर तैर रहा है। कॉर्क को थोड़ा नीचे दबाकर स्वतंत्र छोड़ देते है , यह दर्शाइए की कॉर्क ऊपर - नीचे सरल आवर्त दोलन करता है जिसका आवर्त T=2v√hρρ1g है।
यहाँ ρ कॉर्क का घनत्व है (द्रव की श्यानता के कारण अवमंदन को नगण्य मानिए)
View SolutionA cylindrical piece of cork of density rho , base area A and height h, floats in a liquid of density rho_(1) . The cork is depressed slightly and then released. Show that the cork oscillates up and down simple harmonically, with a period T=2pisqrt((hrho)/(rho_(1)g)) , where 'rho' is the density of the cork.
View SolutionA cylindrical piece of cork of density of base area A and height h floats in a liquid of density pl. The cork is depressed slightly and then released. Show that the cork oscillates up and down simple harmonically with a period
T=2π√hpp1g
where p is the density of cork. (Ignore damping due to viscosity of the liquid).
View SolutionA cylindrical piece of cork of base area A and height h floats in a liquid of density rho_(1) . The cork is depressed slightly and then released. Show that the cork oscillates up and down simple harmonically with a period T=2pisqrt((hrho)/(rho_(1)g))
View SolutionA cylindrical piece of cork of density of base area A and height h floats in a liquid of density pl. The cork is depressed slightly and then released. Show that the cork oscillates up and down simple harmonically with a period
T=2π√hpp1g
where p is the density of cork. (Ignore damping due to viscosity of the liquid).
View SolutionA cylindrical piece of cork of density of base area A and height h floats in a liquid of density ρ1. The cork is depressed slightly and then released. The cork oscillates up and down simple harmonically with period is (ρ is the density of cork)
View SolutionA cylindrical piece of cork of density of base area A and height h floats in a liquid of density p_(l) . The cork is depressed slightly and then released. Show that the cork oscillates up and down simple harmonically with a period T=2pisqrt((hp)/(p_(1)g)) where p is the density of cork. (Ignore damping due to viscosity of the liquid).
View Solution
