A thin uniform spherical shell of mass $m = 2 k g$ and radius $R = 10 c m$ is placed on a rough horizontal surface with a coefficient of friction $μ = 0.4$ . A horizontal force 'F' is applied to the spherical shell at a height $R / 3$ ablove the centre as shown. The maximum magnitude of the applied force 'F' for which the spherical shell will be rolling without slipping is (taking $g = 10 m / a^{2}$ )

A

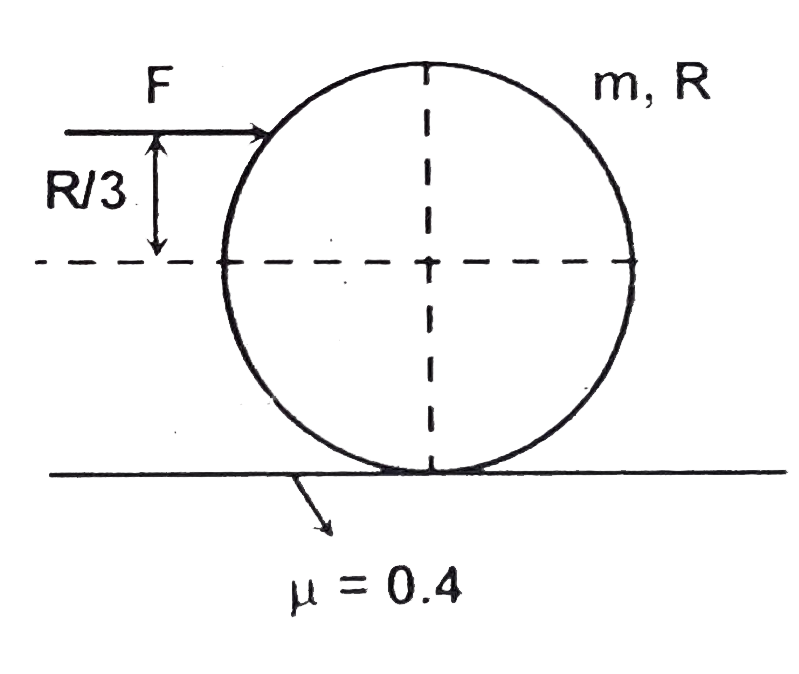
$20 N$

B

$30 N$

C

$40 N$

D

$60 N$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

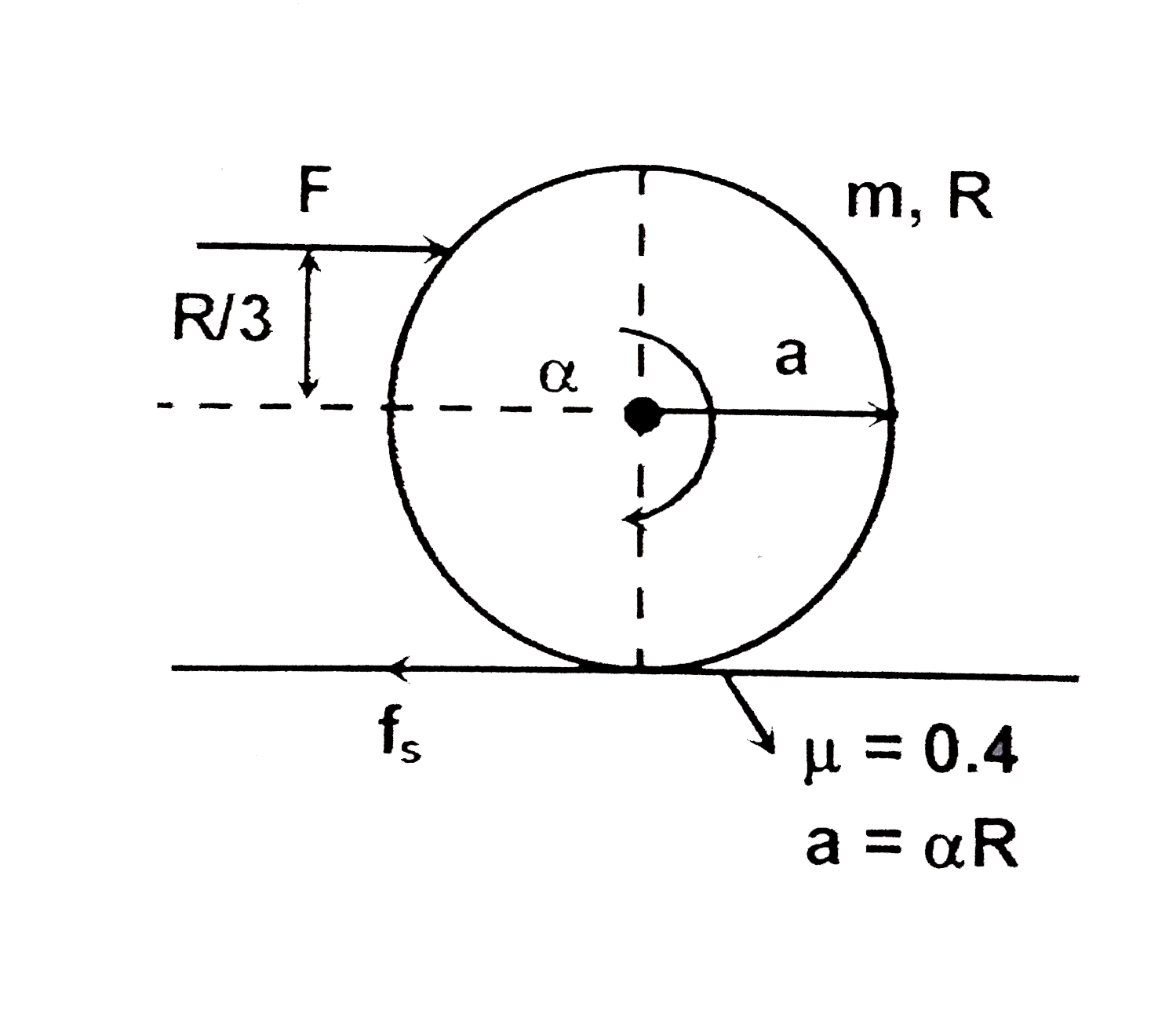
$F - f_{s} = m a$ …..(i)
$\frac{F R}{3} + f_{s} R = \frac{2}{3} m R^{2} α$
$\frac{F}{3} + f_{s} = \frac{2}{3} m a$ [since, $a = R α$ ] …..(i)
Solving (i) and (ii), we get
$\frac{4 F}{3} = \frac{5}{3} m a$
$a = \frac{4 F}{5 m}$
Now, from equation (i)
$f_{s} = F - m a = F - \frac{4 F}{5} = \frac{F}{5}$
Hence, $f_{s} \leq μ N$
$F / 5 \leq μ N$
$F \leq 5 μ m g$
$∴ F_{max} = 5 \times 0.4 \times 20 = 40 N$

Updated on:21/07/2023

|

Class 12 PHYSICS QUESTION BANK

Similar Questions

Recommended Questions

Home
Ask Doubt
Profile