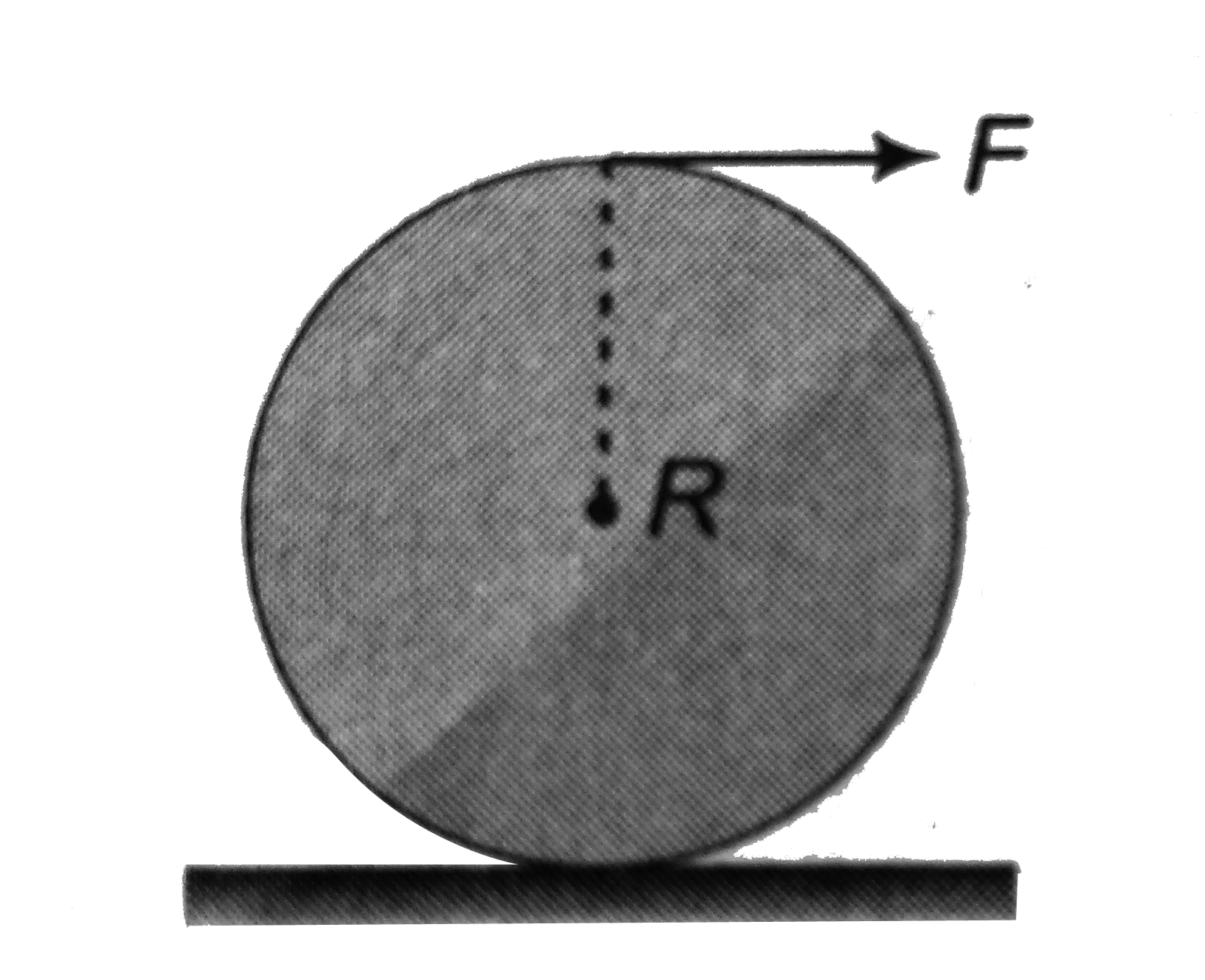
A tangential force $F$ acts at the top of a thin spherical shell of mass $m$ and radius $R$ . Find the acceleration of the shell if it rolls without slipping.

Video Solution

Text Solution

Verified by Experts

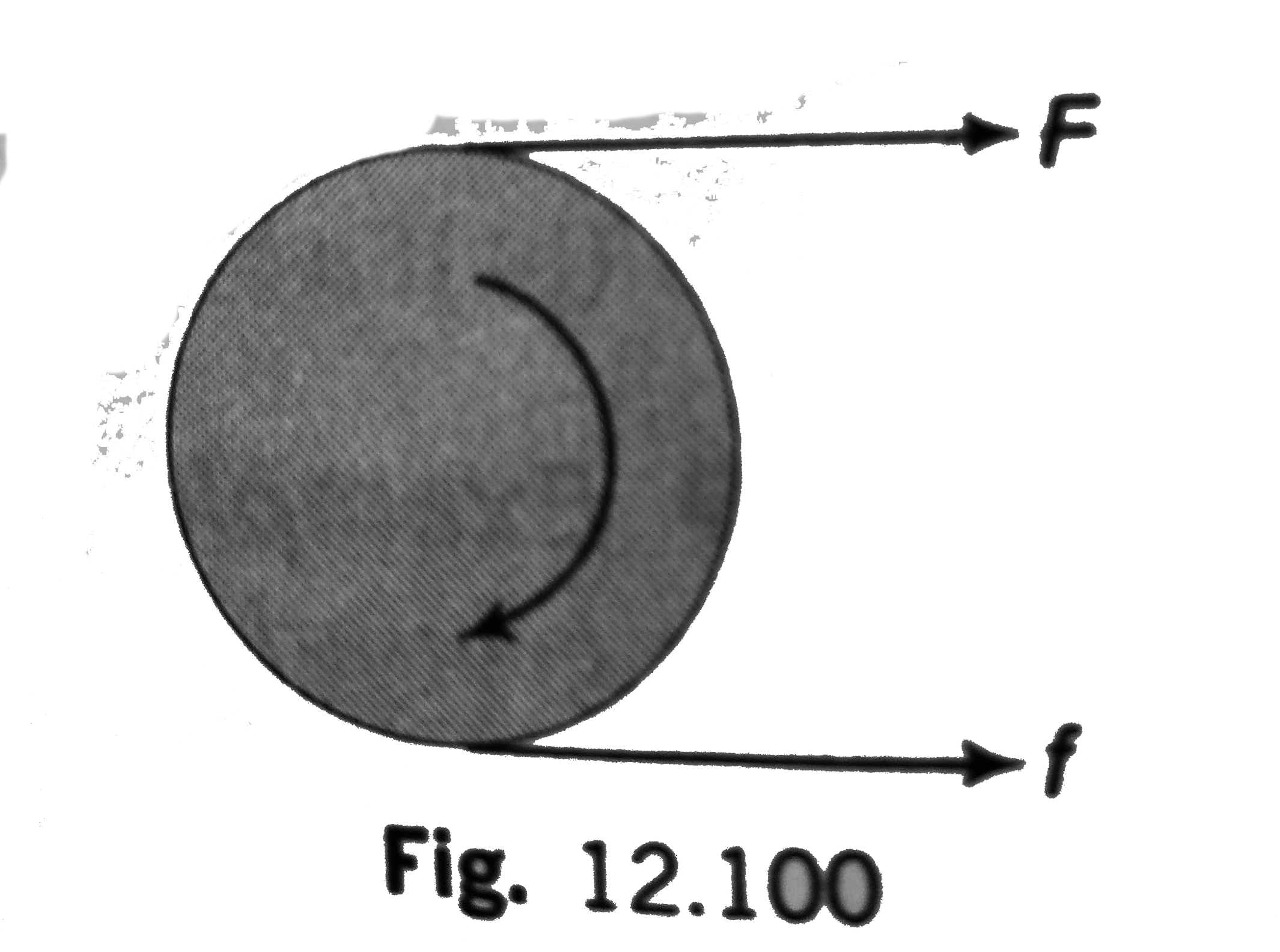Let $f$ be the force of friction between the shell and the horizontal surface.
Force translational motion
$F = f = m a$ ..(i)
For translational motion,
$F R - f R = I α = I \frac{a}{R}$
$[∵ a = R α$ for pure rolling]
Adding eqs. (i) and (ii) we get
$2 F = (m + \frac{I}{R^{2}}) a$
$= (m + \frac{2}{3} m) a = \frac{5}{3} m a$
or $F = \frac{5}{6} m a$ $[∵ I_{shell} = \frac{2}{3} m R^{2}]$
$\Rightarrow a = \frac{6 F}{5 m}$

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One or More
Consider $a$ thin spherical shell of uniform density of mass $M$ and radius $R$ :
AThe gravitational field inside the shell will be zero
BThe gravitational self energy of shell is $\frac{G M^{2}}{2 R}$
CAttractive force experience by unit area of the shell pull the other half is $\frac{G M^{2}}{2 R^{2}}$
DNet gravitational force with which one hemisphere of the shell arracts other, is $\frac{G M^{2}}{8 R^{2}}$
Question 2 - Select One
A thin spherical shell of mass $M$ and radius $R$ has a small hole. A particle of mass $m$ released at its mouth. Then
Athe particle will execute $S . H . M$ inside the shell
Bthe particle will oscillate inside the shell, but the oscillations are not simple harmonic
Cthe particle will not oscillate, but the speed the particle will go on increasing
Dnone ot these
Question 3 - Select One
A block of mass m is lying at a distance r from a spherical shell of mass m and radius r, then :

AOnly gravitational field inside the shell is zero
BGravitational field and gravitational potential both are zero inside the shell
CGravitational potential as well as gravitational field inside the shell are not zero
DCan't be ascertained.

DC PANDEY-ROTATIONAL MECHANICS-Subjective Questions

Home
Ask Doubt
Profile