A body of mass m is placed at the centre of the spherical shell of radius R and mass M. The gravitation potential on the surface of the shell is
−GH(M+m)
−GH(M−m)
−GH(mMM+m)
−GH(mMM−m)
The correct Answer is:A
To solve the problem of finding the gravitational potential on the surface of a spherical shell with a mass M and radius R, while a body of mass m is placed at the center, we can follow these steps:
Step 1: Understand the Concept of Gravitational Potential
Gravitational potential V at a point in a gravitational field is defined as the work done in bringing a unit mass from infinity to that point without any acceleration. The formula for gravitational potential due to a mass M at a distance r is given by:
V=−GMr
where G is the universal gravitational constant.
Step 2: Analyze the Spherical Shell
According to the shell theorem, a uniform spherical shell of mass M exerts no net gravitational force on a mass located inside it. Therefore, the gravitational potential inside the shell (including at the center) is constant and equal to the potential at the surface of the shell.
Step 3: Calculate the Gravitational Potential at the Surface
To find the gravitational potential at the surface of the spherical shell, we need to use the formula for gravitational potential at a distance R from the center (which is also the radius of the shell):
Vsurface=−GMR
Step 4: Consider the Mass m at the Center
The mass m at the center does not affect the potential on the surface of the shell due to the shell theorem. Thus, we only consider the mass M of the shell for calculating the potential at the surface.
Step 5: Final Expression for Gravitational Potential
The gravitational potential on the surface of the shell is given by:
V=−GMR
This is the final answer for the gravitational potential on the surface of the spherical shell.
Summary
The gravitational potential on the surface of the spherical shell is:
V=−GMR
Gravitational potential V at a point in a gravitational field is defined as the work done in bringing a unit mass from infinity to that point without any acceleration. The formula for gravitational potential due to a mass M at a distance r is given by:
According to the shell theorem, a uniform spherical shell of mass M exerts no net gravitational force on a mass located inside it. Therefore, the gravitational potential inside the shell (including at the center) is constant and equal to the potential at the surface of the shell.
To find the gravitational potential at the surface of the spherical shell, we need to use the formula for gravitational potential at a distance R from the center (which is also the radius of the shell):
The mass m at the center does not affect the potential on the surface of the shell due to the shell theorem. Thus, we only consider the mass M of the shell for calculating the potential at the surface.
The gravitational potential on the surface of the shell is given by:
The gravitational potential on the surface of the spherical shell is:
Topper's Solved these Questions
Similar Questions
A particle of mass M is placed at the centre of a uniform spherical shell of equal mass and radius a. Find the gravitational potential at a point P at a distance a2 from the centre.
View SolutionA mass of 50 kg is placed at the centre of a uniform spherical shell of mass 100 kg and radius 50 m. If the gravitational potential at a point, 25 m from the centre is V kg/m. The value of V is:
View Solution
Knowledge Check
A particel of mass M is placed at the centre of a inform spherical shell of mass 2M and radius R. The gravitational potential on the surface of the shell is
A−GMRB−3GMRC−2GMRDzeroA particle of mass m is placed at the centre of a unifrom spherical shell of mass 3 m and radius R The gravitational potential on the surface of the shell is .
A−GmRB−3GmRC−4GmRD−2GmRA particle of mass M is situated at the centre of a spherical shell of same mass and radius 'a'. The gravitational potential at a point situated at a2 distance from the centre, will be
A−3GMaB−2GMaC−GMaD−4GMa
A point mass m0 is placed at distance R/3 from the centre of spherical shell of mass m and radius R. the gravitational force on the point mass m0 is
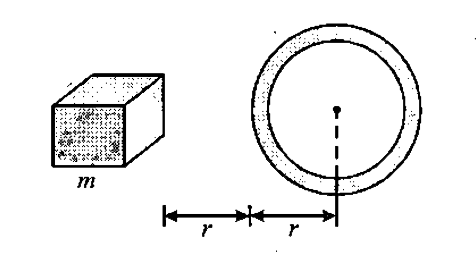
View SolutionA block of mass m is lying at a distance r from a spherical shell of mass m and radius r, then :
View SolutionA point charge q is placed at a distance of r from the centre O of an uncharged spherical shell of inner radius R and outer radius 2R. The electric potential at the centre of the shell will be

View SolutionA point mass m is placed inside a spherical shell of radius R and mass M at a distance R2 form the centre of the shell. The gravitational force exerted by the shell on the point mass is
View SolutionA point mass 'm' is placed inside a spherical shell of radius 'R' and mass 'M' at a distance from the centre of the shell. The gravitational force exerted by the shell on the point mass is -
View Solution

