
For a damped oscillator which follow the equation
the mass of the block is 100 gm K=100N/M and the damping constant is 20 gm/sec. thhen find the time taken for its mechanical energy to drop to one-fourth of its initial value.
1.73
3.46
6.93
13.84
The correct Answer is:C
taking log and solving we get
Similar Questions
For the damped oscillator shown in Figure, the mass m of the block is 400 g, k=45Nm−1 and the damping constant b is 80gs−1. Calculate .
(a) The period of osciallation ,
(b) Time taken for its amplitude of vibrations to drop to half of its initial value and
(c ) The time taken for its mechanical energy to drop to half its initial value.
View SolutionFor the small damping oscillator, the mass of the block is 500 g and value of spring constant is k = 50 N/m and damping constant is 10gs^(-1) The time period of oscillation is (approx.)
View Solution
Knowledge Check
A block of mass 200 g executing SHM under the influence of a spring of spring constant k=90Nm−1 and a damping constant b=40gs−1. The time elapsed for its amplitude to drop to half of its initial value is (Given, ln (1/2)=−0.693)
A7sB9sC4sD11s
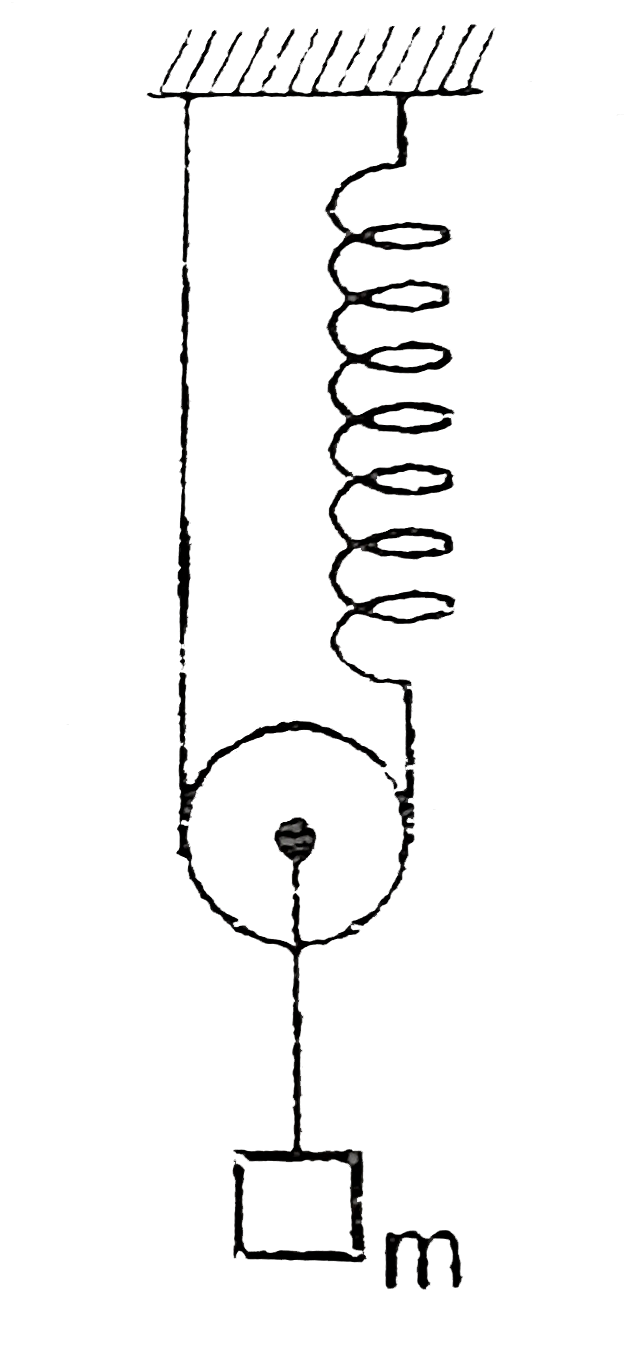
The system is released from rest with spring intially in its natural length. If mass of the block m = 10 kg. and spring constant k=100N/m, then maximum extension in spring is :
View SolutionThe displacement of a damped harmonic oscillator is given by
x(t)−e−0.1tcos(10πt+φ).Here t is in seconds.
The time taken for its amplitude of vibration to drop to half of its initial value is close to :
View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionThree rods AB,BC and BD of same length l and cross sectional area A are arranged as shown. The end D is immersed in ice whose mass is 440 gm. Heat is being supplied at constant rate of 200 cal /sec from the end A. Find out time (in sec) in which wholeice will melt. (latent heat of fusion of ice is 80 cal/gm)
Given k (thermal conductivity) =100 cal/m/sec/∘C,A=10cm2,l=1m
View Solution
A block of mass m is pushed against a spring of spring constant k fixed at one end to a wall.The block can slide on a frictionless table as shown in the figure. The natural length of the spring is L0 and it is compressed to one fourth of natural length and the block is released.Find its velocity as a function of its distance (x) from the wall and maximum velocity of the block. The block is not attached to the spring.
View SolutionA block with a mass of 2kg hangs without vibrating at the end of a spring of spring constant 500N/m, which is attached to the ceiling of an elevator. The elevator is moving upwards with an acceleration g3. At time t=0, the acceleration suddenly ceases.
(a) What is the angular frequency of oscillation of the block after the acceleration ceases ?
(b) By what amount is the spring stretched during the time when the elevator is accelerating ?
(c )What is the amplitude of oscillation and initial phase angle observed by a rider in the elevator in the equation, x=Asin(ωt+ϕ) ? Take the upward direction to be positive. Take g=10.0m/s2.
View SolutionYou are riding an automobile of mass 3000kg. Assuming that you are examining the oscillation characteristics of its suspension system. The suspension sags 15cm when the entire automobile is placed on it. Also, the amplitude of oscillation decreases by50% during one complete oscillation. Estimate the values of (a) the spring constant k and (b) damping constant b for the spring and shock absorber system of one wheel, assuming that each wheel supports 750kg.g=10m/s2.
View Solution
