For the damped oscillator shown in Fig. 14.19, the mass m of the block is 200 g, k = 90 N m−1 and the damping constant b is 40 g s−1. Calculate (a) the period of oscillation, (b) time taken for its amplitude of vibrations to drop to half of its initial value, and (c) the time taken for its mechanical energy to drop to half its initial value.Solution in Gujrati
(a) We see that km = 90x×0.2=18kgNm−1=kg2s−2, therefore √km=4.243kgs−1, and b=0.04kgs−1. Therefore, b is much less than √km . Hence, the time period T from Eq. (14.34) is given by
T=2π√mk
=2π√0.2kg90Nm−1
= 0.3 s
(b) Now, from Eq. (14.33), the time, T1/2, for the amplitude to drop to half of its initial value is given by
T1/2=ln(1/2)b/2m
=0.69340×2×200s
=6.93s
(c) For calculating the time, t1/2, for its mechanical energy to drop to half its initial value we make use of Eq. (14.35). From this equation we have,
E(t1/2/E(0)=exp(−bt1/2/m)
Or 1/2=exp(−bt1/2/m)
ln(1/2)=−(bt1/2/m)
Or t1/2=0.69340gs−1×200g
=3.46 s
This is just half of the decay period for amplitude. This is not surprising, because, according to Eqs. (14.33) and (14.35), energy depends on the square of the amplitude. Notice that there is a factor of 2 in the exponents of the two exponentials.
Topper's Solved these Questions
- OSCILLATIONSBOOK - NCERT GUJARATICHAPTER - OSCILLATIONSEXERCISE - Exercises
28 Videos
- OSCILLATIONSBOOK - NCERT GUJARATICHAPTER - OSCILLATIONSEXERCISE - Additional Exercises
6 Videos
- MOTION IN A STRAIGHT LINEBOOK - NCERT GUJARATICHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ADDITIONAL EXERCISES
5 Videos
- PHYSICAL WORLD BOOK - NCERT GUJARATICHAPTER - PHYSICAL WORLD EXERCISE - EXERCISES
8 Videos
Similar Questions
Which of the following examples represent periodic motion?
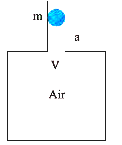
View SolutionAn air chamber of volume V has a neck area of cross section a into which a ball of mass m just fits and can move up and down without any friction (Fig.14.27). Show that when the ball is pressed down a little and released , it executes SHM. Obtain an expression for the time period of oscillations assuming pressure-volume variations of air to be isothermal [see Fig. 14.27].
View SolutionA boy standing on a stationary lift (open from above) throws a ball upwards with the maximum initial speed he can equal to 49 ms-1. How much time does the ball take to return to his hands ? If the lift starts moving up with a uniform speed of 5 ms−1 and the boy again throws the ball up with the maximum speed he can, how long goes the ball take to return to his hands ?
View SolutionSome of the most profound statements on the nature of science have come from Albert Einstein, one of the greatest scientists of all time. What do you think did Einstein mean when he said: "The most incomprehensible thing about the world is that it is comprehensible" ?
View SolutionIn damped oscillatory motion a block of mass 20kg is suspended to a spring of force constant 90N//m in a medium and damping constant is 40g//s . Find (a) time period of oscillation (b) time taken for amplitude of oscillation to drop to half of its intial value (c) time taken for its mechanical energy to drop to half of its initial value.
View SolutionFor the damped oscillator shown in Fig, the mass of the block is 200 g, k = 80 N m^(-1) and the damping constant b is 40 gs^(-1) Calculate (a) The period of oscillation (b) Time taken for its amplitude of vibrations to drop to half of its initial values (c) The time for the mechanical energy to drop to half initial values
View Solutionचित्र 14.19 में दर्शाए अवमंदित दोलन के लिए घुटके का द्रव्यमानm = 200 g, k=90Nm−1 तथा अवमंदन स्थिरांक b=40gs−1 है | (a) दोलन का आवर्तकाल, (b) वह समय जिसमें इसके कंपन का आयाम अपने आरंभिक मान का आधा रह जाता है तथा (c) वह समय जिसमें यांत्रिक ऊर्जा अपने आरंभिक मान की आधी रह जाती है, परिकलित कीजिए |
View SolutionFor the damped oscillator shown in previous Figure, the mass m of the block is 400 g, k=45 Nm^(-1) and the damping constant b is 80 g s^(-1) . Calculate . (a) The period of osciallation , (b) Time taken for its amplitude of vibrations to drop to half of its initial value and (c ) The time taken for its mechanical energy to drop to half its initial value.
View SolutionFor a damped oscillation of a particle, show that time taken for the amplitude to drop to half of its initial value =2mln(2)b, where b is a damping constant.
View SolutionCalculate the time taken for particele energy to drop to half its initial value in the case of a damped oscillator.
View SolutionFor a damped oscillator. The mass of the block is 200 g. k=90 N.m^-1 and the damping constant b is 40 g. s^-1 . Calculate the period of oscillation.
View SolutionFor the damped oscillator of Fig. 15.20, m= 250g, k= 85N/m, and b= 70g/s
How long does it take for the amplitude of the damped oscillations to drop to half its initial value?
View SolutionFor the damped oscillator shown in Fig. 14.19, the mass m of the block is 200 g, k = 90 N m^(-1) and the damping constant b is 40 g s^(-1) . Calculate (a) the period of oscillation, (b) time taken for its amplitude of vibrations to drop to half of its initial value, and (c) the time taken for its mechanical energy to drop to half its initial value.
View SolutionFor the damped oscillator, the mass m of the block is 200g,k=90Nm−1 and the damping constant b is 40gs−1. Calculate time taken for its amplitude of vibrations to drop to half of its initial value.
View SolutionFor the damped oscillator, the mass m of the block is 200g,k=90Nm−1 and the damping constant b is 40gs−1. Calculate the time taken for its mechanical energy to drop to half its initial value.
View Solution
