A sperical ball of mass m, radiua r is connected to string of length (l>>r). This string is then connected to fixed point and this arrangement allowed to oscillate in a medium whose density is ρ and viscosity is η. If amplitude of oscillation becomes half of the initial value after n seconds then viscosity of liquid is given by (Assume that resistance force on ball follows stoke's law)
mπrn
mln(21/3)πrn
mln8πrn
mln2πrn
The correct Answer is:B
To solve the problem, we need to find the viscosity of the liquid (η) given that the amplitude of oscillation of a spherical ball becomes half of its initial value after n seconds. We will use the principles of damped oscillations and Stokes' law.
1. Understanding Damped Oscillation:
In damped oscillation, the amplitude A(t) of the oscillation decreases over time. The relationship can be expressed as:
A(t)=A0e−b2mt
where A0 is the initial amplitude, b is the damping coefficient, and m is the mass of the ball.
2. Setting Up the Condition:
According to the problem, after n seconds, the amplitude becomes half of its initial value:
A(n)=A02
Substituting this into the equation gives:
A02=A0e−b2mn
3. Simplifying the Equation:
Dividing both sides by A0 (assuming A0≠0):
12=e−b2mn
4. Taking the Natural Logarithm:
To solve for b, take the natural logarithm of both sides:
ln(12)=−b2mn
This simplifies to:
−ln(2)=−b2mn
or
ln(2)=b2mn
5. Solving for the Damping Coefficient b:
Rearranging gives:
b=2mln(2)n
6. Relating Damping Coefficient to Viscosity:
From Stokes' law, the damping coefficient b for a spherical object in a viscous medium is given by:
b=6πηr
where η is the viscosity and r is the radius of the sphere.
7. Equating the Two Expressions for b:
Set the two expressions for b equal to each other:
6πηr=2mln(2)n
8. Solving for Viscosity η:
Rearranging gives:
η=2mln(2)6πrn
Simplifying this, we get:
η=mln(2)3πrn
Final Answer:
The viscosity of the liquid is given by:
η=mln(2)3πrn
In damped oscillation, the amplitude A(t) of the oscillation decreases over time. The relationship can be expressed as:
A(t)=A0e−b2mt
where A0 is the initial amplitude, b is the damping coefficient, and m is the mass of the ball.
According to the problem, after n seconds, the amplitude becomes half of its initial value:
A(n)=A02
Substituting this into the equation gives:
A02=A0e−b2mn
Dividing both sides by A0 (assuming A0≠0):
12=e−b2mn
To solve for b, take the natural logarithm of both sides:
ln(12)=−b2mn
This simplifies to:
−ln(2)=−b2mn
or
ln(2)=b2mn
Rearranging gives:
b=2mln(2)n
From Stokes' law, the damping coefficient b for a spherical object in a viscous medium is given by:
b=6πηr
where η is the viscosity and r is the radius of the sphere.
Set the two expressions for b equal to each other:
6πηr=2mln(2)n
Rearranging gives:
η=2mln(2)6πrn
Simplifying this, we get:
η=mln(2)3πrn
The viscosity of the liquid is given by:
η=mln(2)3πrn
Similar Questions
Three point charges, each with charge q and mass 'm', are connected by three strings of equal length l whose other end is connected to a fixed point P. They form an equilateral triangle of side 'a' in a horizontal plane. The tension in each string will be
View SolutionTwo block A and B of mass M & 3M are connected through a light string. One end of the string is connected to the blcok B and its other end is connected to a fixed point S as shown in fig. Now a force F is applied to block B. find the acceleration of block A & B.

View SolutionReynolds number for a liquid of density ρ, viscosity η and flowing through a pipe of diameter D, is given by
View SolutionWhen an oscillator completes 50 oscillations its amplitude reduced to half of initial value (A0). The amplitude of oscillation, when it completes 150 oscillations is
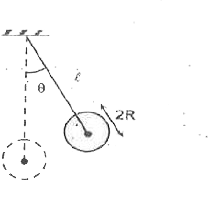
View SolutionA spherical bob of mass m and radius R is attached to a fixed point by means of a massless rigid rod whose length from the point of support up to the centre of bob is l. Find the period of small oscillation.
View SolutionVolume rate flow of a liquid of density ρ and coefficient of viscosity η through a cylindrical tube of diameter D is Q. Reynold's number of the flow is
View SolutionA ball of mass m kept at the centre of a string of length L is pulled from centre in perpendicular direction and released. Prove that motion of ball is simple harmonic and determine time period of oscillation
View SolutionA small ring of mass m1 is connected by a string of length l to a small heavy bob of mass m2. The ring os free to move (slide) along a fixed smooth horizontal wire. The bob is given a small displacement from its equilibrium position at right angles to string. Find period of small oscillations.
_E01_106_Q01.png)
View SolutionA sperical body of mass m and radius r is allowed to fall in a medium of viscosity η. The time in which the velocity of the body increases from zero to 0.63 times the terminal velocity (v) is called constant (τ). Dimensionally , τ can be represented by
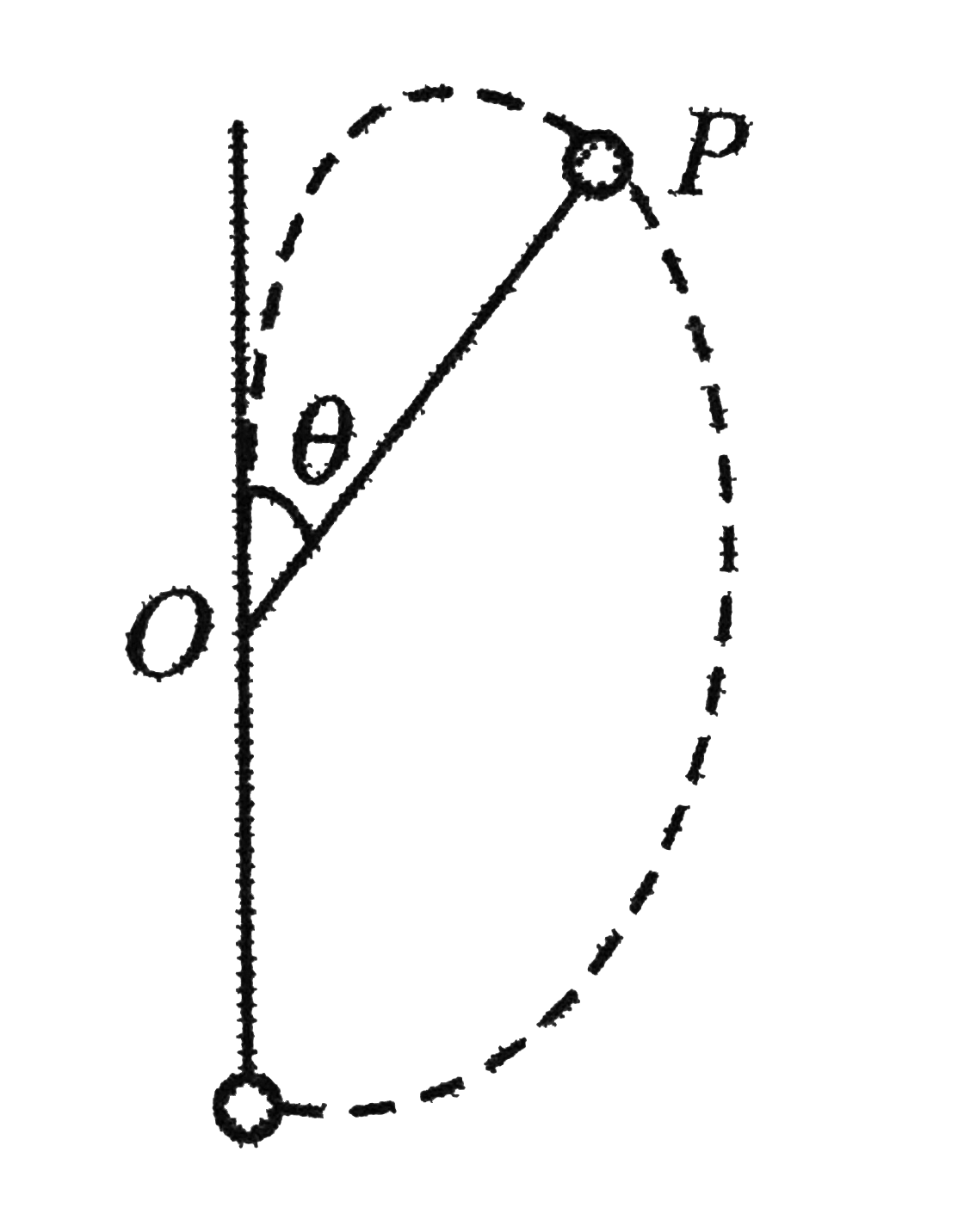
View SolutionA point mass m connected to one end of inextensible string of length l and other end of string is fixed at peg. String is free to rotate in vertical plane. Find the minimum velocity given to the mass in horizontal direction so that it hits the peg in its subsequent motion.
View Solution
