A sperical body of mass m and radius r is allowed to fall in a medium of viscosity η. The time in which the velocity of the body increases from zero to 0.63 times the terminal velocity (v) is called constant (τ). Dimensionally , τ can be represented by
mr26πη
√6πmrηg2
m6πηrv
None of these
The correct Answer is:D
To solve the problem of determining the dimensional representation of the time constant τ for a spherical body falling through a viscous medium, we will analyze the given options step by step.
Step 1: Understanding the Problem
We need to find the dimensional representation of the time constant τ in terms of the parameters given: mass m, radius r, viscosity η, and terminal velocity v.
Step 2: Identifying Dimensions
- Mass m: Dimension is (M)
- Radius r: Dimension is (L)
- Viscosity η: Dimension is (M)(L)−1(T)−2
- Velocity v: Dimension is (L)(T)−1
Step 3: Analyzing Each Option
Option 1: mr26πη
1. Calculate dimensions:
- m: (M)
- r2: (L2)
- η: (M)(L)−1(T)−2
Now, substituting into the expression:
Dimension=(M)(L2)(M)(L)−1(T)−2=(M)(L2)(M)(L−1)(T−2)
Simplifying gives:
=(L3)(T2)=(M0)(L3)(T2)
This does not represent time.
Option 2: √6πmrηg2
1. Calculate dimensions:
- g (acceleration due to gravity): (L)(T)−2
Now substituting into the expression:
Dimension=√(M)(L)(M)(L)−1(T)−2(L2)(T−4)=√(M2)(L0)(T−2)(L2)(T−4)
Simplifying gives:
=√(M2)(L−2)(T2)=(M)(L−1)(T)
This also does not represent time.
Option 3: m6πηrv
1. Calculate dimensions:
- Substitute dimensions:
Dimension=(M)(M)(L)−1(T)−2⋅(L)⋅(L)(T)−1=(M)(M)(L0)(T−3)
Simplifying gives:
=(T3)
This does not represent time.
Conclusion
After analyzing all options, none of them represent the dimension of time (T). Therefore, the conclusion is that none of the options correctly represent the dimensional formula for τ.
We need to find the dimensional representation of the time constant τ in terms of the parameters given: mass m, radius r, viscosity η, and terminal velocity v.
- Mass m: Dimension is (M)
- Radius r: Dimension is (L)
- Viscosity η: Dimension is (M)(L)−1(T)−2
- Velocity v: Dimension is (L)(T)−1
1. Calculate dimensions:
- m: (M)
- r2: (L2)
- η: (M)(L)−1(T)−2
Now, substituting into the expression:
Dimension=(M)(L2)(M)(L)−1(T)−2=(M)(L2)(M)(L−1)(T−2)
Simplifying gives:
=(L3)(T2)=(M0)(L3)(T2)
This does not represent time.
1. Calculate dimensions:
- g (acceleration due to gravity): (L)(T)−2
Now substituting into the expression:
Dimension=√(M)(L)(M)(L)−1(T)−2(L2)(T−4)=√(M2)(L0)(T−2)(L2)(T−4)
Simplifying gives:
=√(M2)(L−2)(T2)=(M)(L−1)(T)
This also does not represent time.
1. Calculate dimensions:
- Substitute dimensions:
Dimension=(M)(M)(L)−1(T)−2⋅(L)⋅(L)(T)−1=(M)(M)(L0)(T−3)
Simplifying gives:
=(T3)
This does not represent time.
After analyzing all options, none of them represent the dimension of time (T). Therefore, the conclusion is that none of the options correctly represent the dimensional formula for τ.
Topper's Solved these Questions
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Multiple Correct
2 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Linked Comprehension
3 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Subjective
31 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - INTEGER_TYPE
1 Video
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - INTEGER_TYPE
1 Video
Similar Questions
A small steel ball of radius r is allowed to fall under gravity through a column of a viscous liquid of coefficient of viscosity η. After some time the velocity of the ball attains a constant value known as terminal velocity υT. The terminal velocity depends on (i) the mass of the ball m (ii) η, (iii) r and (iv) acceleration due to gravity g . Which of the following relations is dimensionally correct?
View SolutionA small steel ball of radius r is allowed to fall under gravity through a column of a viscous liquid of coefficient of viscosity η. After some time the velocity of the ball attains a constant value known as terminal velocity υT. The terminal velocity depends on (i) the mass of the ball m (ii) η, (iii) r and (iv) acceleration due to gravity g . Which of the following relations is dimensionally correct?
View Solution
Knowledge Check
A spherical metal ball of mass m and radius (r) is falling through a viscous medium. The value of its terminal velocity is proportional to
A1/r onlyBm/rC(m/r)1/2Dm onlyA body possesses kinetic energy of 'X'J. If the mass of body increases 49 times determine its final velocity if Kinetic energy remains constant.
A1/5th the original velocityB1/2 the original velocityC1/7th the original velocityD1/X the original velocityA force of 6 N acts on a body at rest and mass 1 kg. During this time, the body attains a velocity of 30 m/s. The time for which the force acts on the body is
A10 secB8 secC7 secD5 sec
A small steel ball of radius r is allowed to fall under gravity through a column of a viscous liquid of coefficient of viscosity η. After some time the velocity of the ball attains a constant value known as terminal velocity υT. The terminal velocity depends on (i) the mass of the ball m (ii) η, (iii) r and (iv) acceleration due to gravity g . Which of the following relations is dimensionally correct?
View SolutionThe motion of a body is represented by the following displacement-time graph.
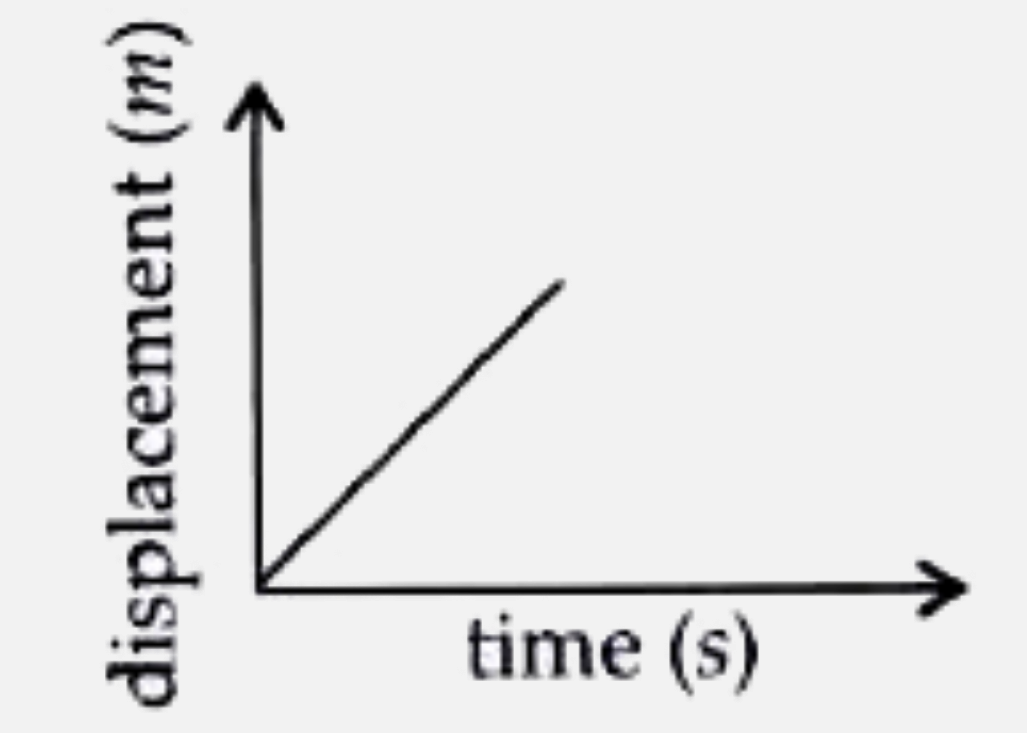
How can the velocity of the body be determined from the above graph?
View SolutionA sphere of mass m and radius r is projected in a gravity free space with speed v. If coefficient of viscosity of the medium in which it moves is 16π , the distance travelled by the body before it stops is
View SolutionA sphere of mass m and radius r is projected in a gravity free space with speed v. If coefficient of viscosity of the medium in which it moves is 16π , the distance travelled by the body before it stops is
View SolutionA body of mass m is moving with a uniform velocity U. A force is applied on the body due to which its velocity increases from u to v: How much work is being done by the force ?
View Solution
