A vibrating system consists of mass 12.5 kg, a spring of spring constant 1000 Nm performing damped oscillation with damping coefficient of 15 kg s−1. The value of critical damping coefficient of the system is
223.6kgs−1
71.4kgs−1
100kgs−1
110kgs−1
The correct Answer is:A
To find the critical damping coefficient (BC) of the given vibrating system, we can follow these steps:
Step 1: Identify the given values
- Mass (m) = 12.5 kg
- Spring constant (k) = 1000 N/m
- Damping coefficient (C) = 15 kg/s (not needed for finding critical damping)
Step 2: Recall the formula for critical damping coefficient
The critical damping coefficient (BC) is given by the formula:
BC=2√k⋅m
Step 3: Substitute the known values into the formula
Now, we will substitute the values of k and m into the formula:
BC=2√1000N/m⋅12.5kg
Step 4: Calculate the product inside the square root
First, calculate the product:
1000⋅12.5=12500
Step 5: Calculate the square root
Now, find the square root of 12500:
√12500=111.8(approximately)
Step 6: Multiply by 2
Now, multiply the square root by 2 to find BC:
BC=2⋅111.8≈223.6kg/s
Final Answer
Thus, the critical damping coefficient of the system is:
BC≈223.6kg/s
- Mass (m) = 12.5 kg
- Spring constant (k) = 1000 N/m
- Damping coefficient (C) = 15 kg/s (not needed for finding critical damping)
The critical damping coefficient (BC) is given by the formula:
BC=2√k⋅m
Now, we will substitute the values of k and m into the formula:
BC=2√1000N/m⋅12.5kg
First, calculate the product:
1000⋅12.5=12500
Now, find the square root of 12500:
√12500=111.8(approximately)
Now, multiply the square root by 2 to find BC:
BC=2⋅111.8≈223.6kg/s
Thus, the critical damping coefficient of the system is:
BC≈223.6kg/s
Topper's Solved these Questions
Similar Questions
A block of mass 0.1 kg attached to a spring of spring constant 400 N/m is putted rightward from x0=0 to x1=15 mm. Find the work done by spring force.
View Solutiona block of mass 0.1 kg attached to a spring of spring constant400Nm pulled horizontally from x=0 tox1=10mm. Find the work done by the spring force
View Solution
Knowledge Check
A system of springs with their spring constants are as shown in figure. What is the frequency of oscillations of the mass m ?
 A12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k4]mB12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mC12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mD12π√(k1+k2)(k3+k4)+k1k2k1k2(k3+k4)m
A12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k4]mB12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mC12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mD12π√(k1+k2)(k3+k4)+k1k2k1k2(k3+k4)m
A block of mass 0.2 kg is attached to a mass less spring of force constant 80 N/m as shown in figure. Find the period of oscillation. Take g=10m/s2. Neglect friction

View SolutionA block of mass 0.2 kg is attached to a mass less spring of force constant 80 N/m as shown in figure. Find the period of oscillation. Take g=10m/s2. Neglect friction

View SolutionTwo uniform discs A and B of equal radii but having different masses 1 kg and 2 kg respectively, are connected (at centres) by a massless spring of spring constant k=1000Nm−1 and then placed on a sufficiently rough horizontal surface. If initially, the system is released from rest with the spring being compressed by 10 cm, then the speed of A when the spring comes back to its natural length, is

View SolutionFor the small damping oscillator, the mass of the block is 500 g and value of spring constant is k = 50 N/m and damping constant is 10gs^(-1) The time period of oscillation is (approx.)
View SolutionFree end of an ideal spring of spring constant 100 N/m is at a distance 1 m from a vertical block of mass 2 kg moving on rough surface with initial speed 8 m/s as shown in figure. If coefficient of friction is 0.7, then maximum compression in spring is (g=10ms−2)
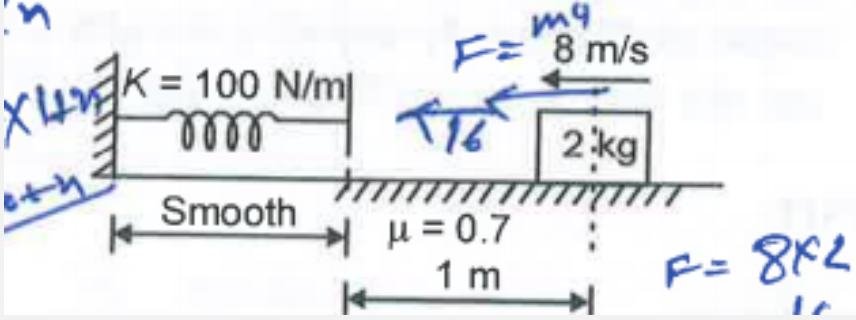
View SolutionTwo masses 8 kg 4 kg are suspended together by a massless spring of spring constant 1000Nm−1 . When the masses are in equilibrium 8 kg is removed without disturbing the system . The amplitude of oscillation is
View SolutionA small block of mass 2 kg is placed on a bigger block of mass 4 kg which is attached to horizontal spring of spring constant K=500N/m as shown in figure, coefficient of friction between block is 0.2 .Maximum amplitude of system so that there is no relative slipping between blocks.
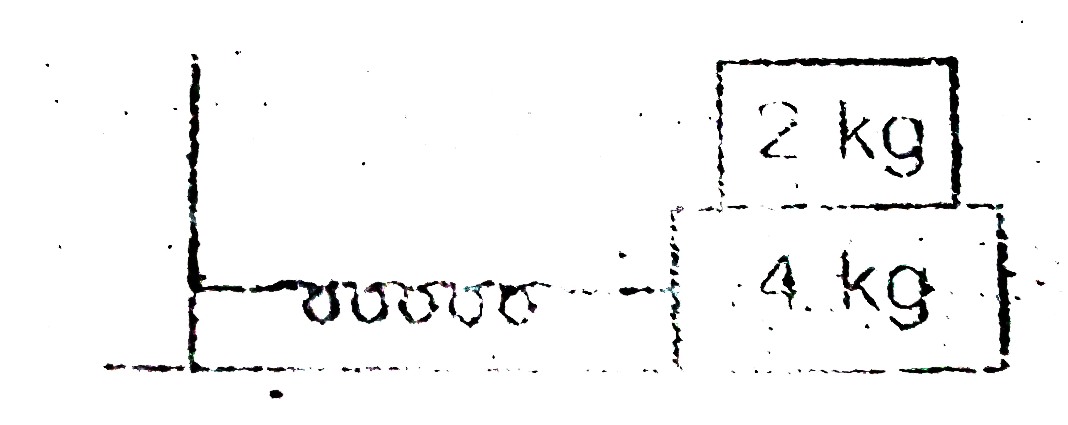
View Solution