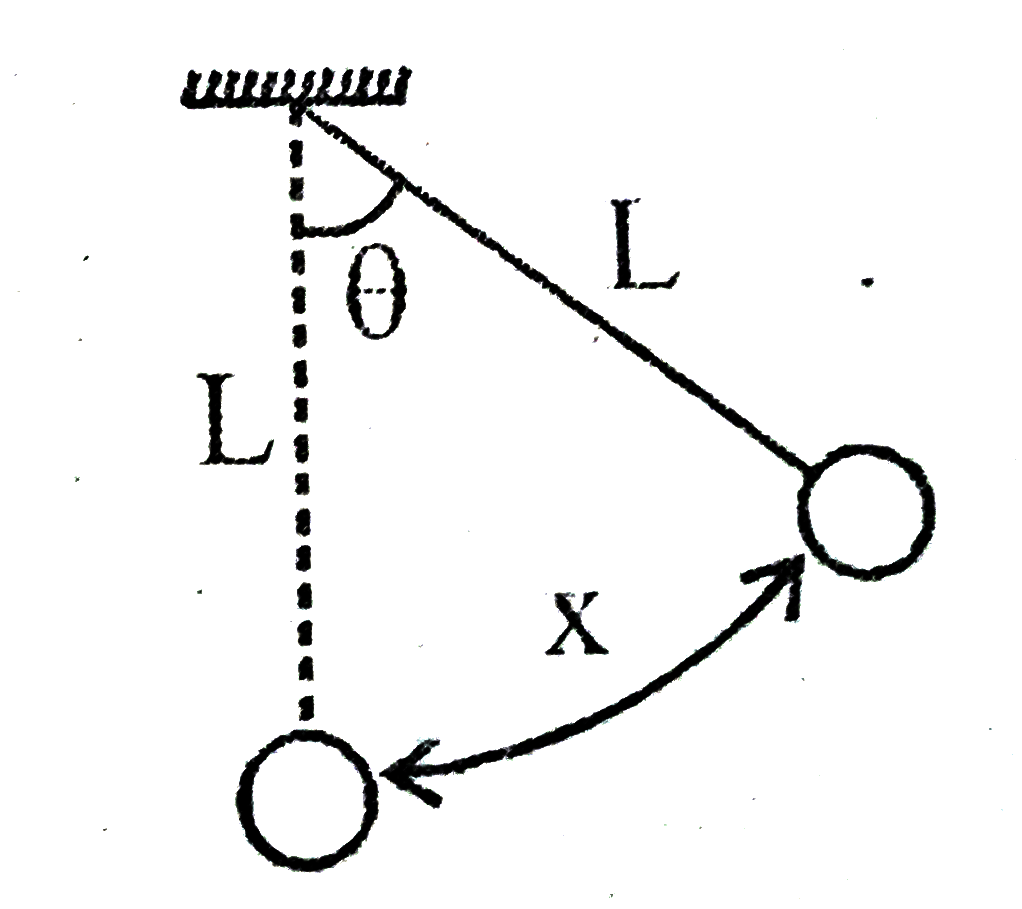
The bob in a simple pendulum of length l is released at t=0 from the of small angular displacement θ0. Linear displacement of the bob at any time t from the mean position is given by :
x=θ0sin2π√(L/g)t
x=Lθ0cos2π√(g/L)t
x=Lθ0sin√(g/L)t
x=Lθ0cos√(g/L)t
The correct Answer is:D
As pendulum starts from EP
So equation of SHM is
θ=θ0cosωt where ω=2πT
ω=2π2π√Lg=√gL
⇒θ=θ0cos√gLt
At time t
Linear displacement = x=Lθ
x=Lθ0cos√gLt
Topper's Solved these Questions
Similar Questions
The bob of a simple pendulum of length L is released at time t = 0 from a position of small angular displacement θ0 . Its linear displacement at time t is given by :
View SolutionA simple pendulum of length l has a maximum angular displacement θ. The maximum kinetic energy of the bob of mass m will be
View SolutionA simple pendulum of length l has maximum angular displacement θ . Then maximum kinetic energy of a bob of mass m is
View SolutionA pendulum of length l=1m is released from θ0=60∘ . The rate of change of speed of the bob at θ=30∘ is.
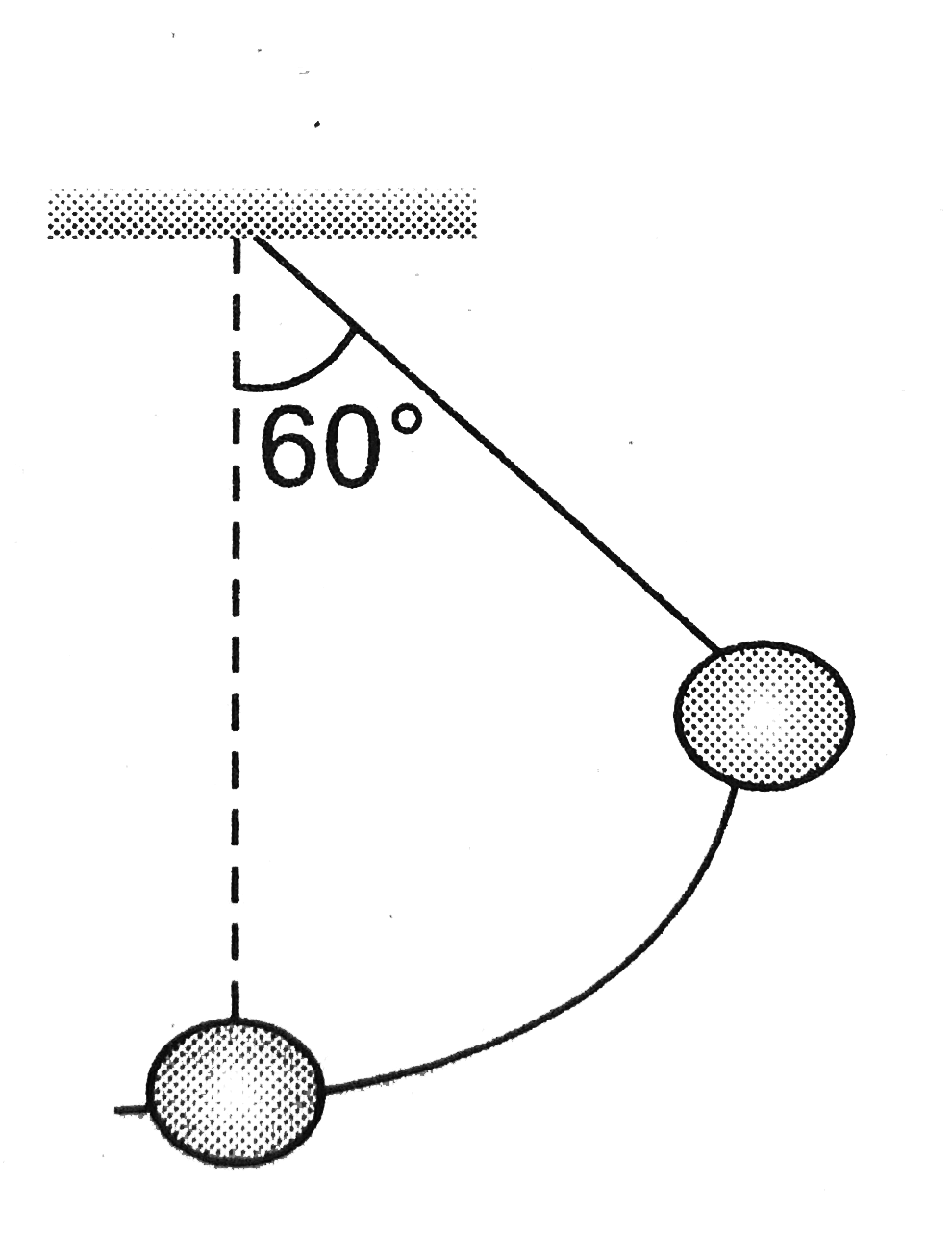
View SolutionA pendulum of length l=1m is released from θ0=60∘ . The rate of change of speed of the bob at θ=30∘ is.

View SolutionA simple pendulum of length L and mass M is oscillating about a vertical line with angular amplitude θ. If for an angular displacement ϕ(ϕ>θ) the tension in the string is T1 and for angular amplitude θ the tension is T2, then
View SolutionA bob hangs from a rigid support by an inextensible string of length l. It is released from rest when string makes an agngle 60∘ with vertical . The speed of the bob at the lowest position is
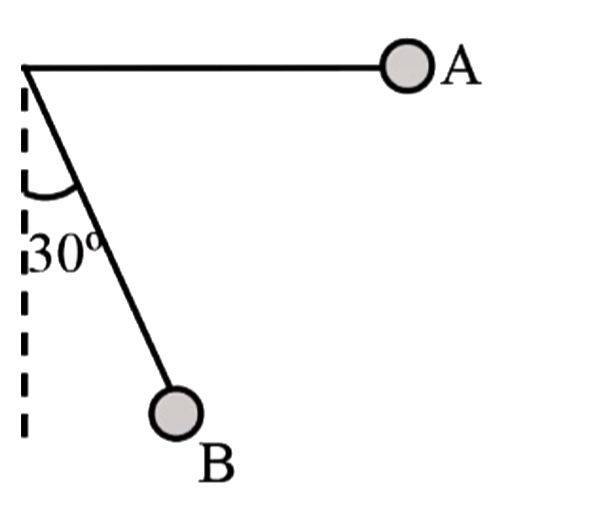
View SolutionA simple pendulum is released from A as shown. If m and 1 represent the mass of the bob and length of the pendulum, the gain kinetic energy at B is
View SolutionThe string of pendulum of length l is displaced through 90∘ from the vertical and released. Then the minimum strength of the string in order to withstand the tension, as the pendulum passes through the mean position is
View SolutionA simple pendulum of mass m and length L is held in horizontal position. If it is released from this position, then find the angular momentum of the bob about the point of suspension when it is vertically below the point of suspension.
View Solution
