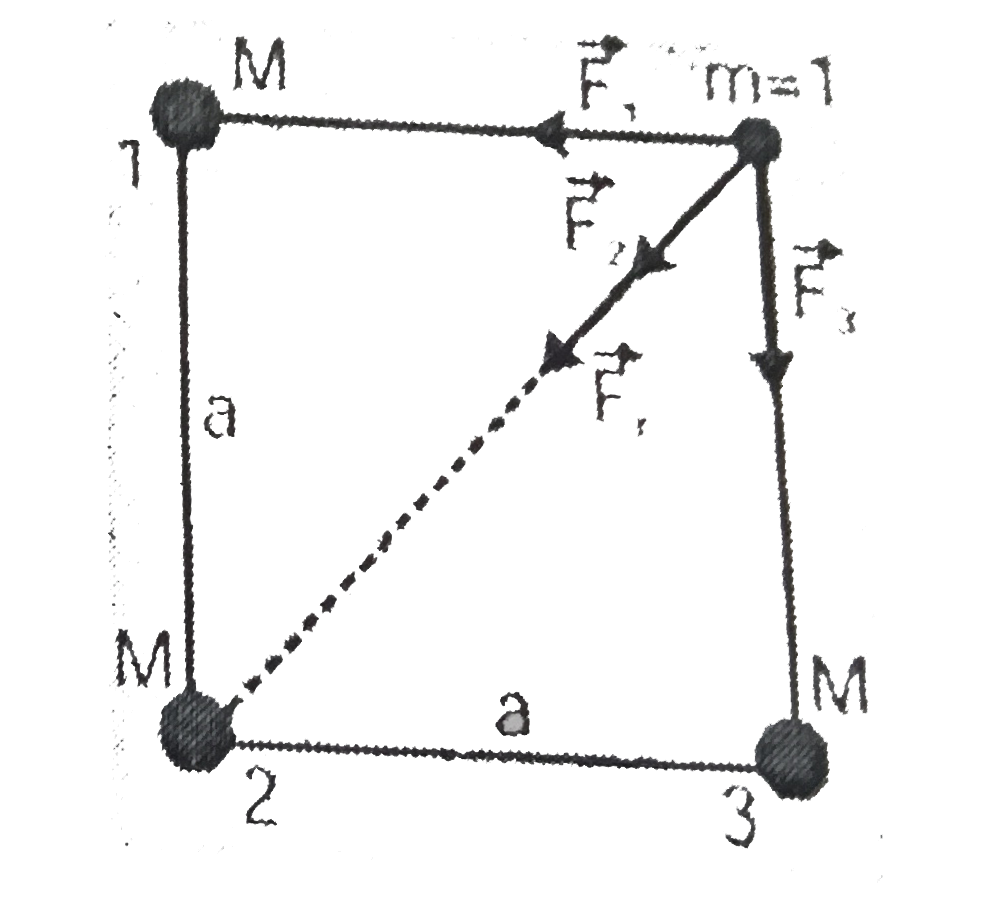
Three masses, each equal to M are placed at the three corners of a square of side a. Calculate the force of attraction on unit mass at the fourth corner.

Video Solution

Text Solution

Verified by Experts

Force on $m = 1$ due to masses at corners 1 and 3 are $- \to F_{1}$ and $- \to F_{3}$ with $F_{1} = F_{3} = \frac{G M}{a^{2}}$ resultant of $- \to F_{1}$ and $- \to F_{3}$ is $F_{r} = \sqrt{2} \frac{G M}{a^{2}}$ and its direction is along the diagonal i.e. towards corner 2
Force on m due to mass M at 2 is $F_{2} = \frac{G M}{{(\sqrt{2} a)}^{2}} = \frac{G M}{2 a^{2}}, F_{r}$ and $F_{2}$ act in the same direction. Resultant of these two is the net force :
$F_{net} = \frac{\sqrt{2} G M}{a^{2}} + \frac{G M}{2 a^{2}} = \frac{G M}{a^{2}} [\sqrt{2} + \frac{1}{2}]$ , It is directed along the diagonal as shown in the figure.

Updated on:21/07/2023

Six point masses of mass $m$ each are at the vertices of a regular hexagon of side $l$ . Calculate the force on any of the masses.
A $\frac{G m^{2}}{l^{2}} [\frac{5}{4} + \frac{1}{\sqrt{3}}]$
B $\frac{G m^{2}}{l^{2}} [\frac{3}{4} + \frac{1}{\sqrt{3}}]$
C $\frac{G m^{2}}{l^{2}} [\frac{5}{4} - \frac{1}{\sqrt{3}}]$
D $\frac{G m^{2}}{l^{2}} [\frac{3}{4} - \frac{1}{\sqrt{3}}]$