A projectile is thrown from a point in a horizontal plane such that the horizontal and vertical velocities are and . It will strike the plane after covering distance of
4.9m
9.8m
19.6m
39.2m
The correct Answer is:D
To solve the problem of how far the projectile will travel before striking the ground, we can follow these steps:
Step 1: Identify the given values
- Horizontal velocity (u_x) = 9.8 m/s
- Vertical velocity (u_y) = 19.6 m/s
- Acceleration due to gravity (g) = 9.8 m/s²
Step 2: Calculate the time of flight
The time of flight (T) for a projectile can be calculated using the formula:
T=2⋅uyg
Substituting the values:
T=2⋅19.69.8=39.29.8=4 seconds
Step 3: Calculate the horizontal distance (range)
The horizontal distance (R) covered by the projectile can be calculated using the formula:
R=ux⋅T
Substituting the values:
R=9.8⋅4=39.2 meters
Step 4: Conclusion
The projectile will strike the plane after covering a distance of 39.2 meters.
---
- Horizontal velocity (u_x) = 9.8 m/s
- Vertical velocity (u_y) = 19.6 m/s
- Acceleration due to gravity (g) = 9.8 m/s²
The time of flight (T) for a projectile can be calculated using the formula:
T=2⋅uyg
Substituting the values:
T=2⋅19.69.8=39.29.8=4 seconds
The horizontal distance (R) covered by the projectile can be calculated using the formula:
R=ux⋅T
Substituting the values:
R=9.8⋅4=39.2 meters
The projectile will strike the plane after covering a distance of 39.2 meters.
Topper's Solved these Questions
- MOTION IN A PALNEBook:ALLENChapter:MOTION IN A PALNEExercise:EXERCISE-3
Explore 40 Videos
- MOTION IN A PALNEBook:ALLENChapter:MOTION IN A PALNEExercise:SOLVED EXAMPLE
Explore 28 Videos
- MOTION IN A PALNEBook:ALLENChapter:MOTION IN A PALNEExercise:EXERCISE-1
Explore 99 Videos
- KINEMATICS-2DBook:ALLENChapter:KINEMATICS-2DExercise:Exercise (O-2)
Explore 46 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBook:ALLENChapter:NEWTON'S LAWS OF MOTION & FRICTIONExercise:EXERCISE (JA)
Explore 4 Videos
Similar Questions
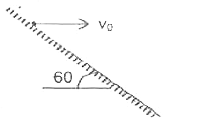
A ball is projected horizontally from an inclined plane with a velocity V, as shown in the figure. It will strike the plane after a time
View SolutionA ball is projected from a point in a horizontal plane so as to strike a vertical wall at right angle A.after rebounding from the wall it strikes the horizontal plane once and returns to the point of projection just before second collision at horizontal surface. Find co-efficient of restitution for the two collisions, assuming it to be same for both the collision.
View SolutionA projectile is thrown upward with a velocity v0 at an angle α to the horizontal. The change in velocity of the projectile when it strikes the same horizontal plane is
View SolutionA projectile is thrown in the upward direction making an angle of 60∘ with the horizontal direction with a velocity of 150ms−1. Then the time after which its inclination with the horizontal is 45∘ is
View SolutionTwo particles are thrown horizontally in opposite directions from the same point from a height h with velocities 4ms−1and3ms−1 . What is the separation between them when their velocities are perpendicular to each other?
View SolutionA ball is thrown from a point O aiming a target at angle 30∘ with the horizontal so that the ball hits the target at B but the ball hits at point A, a vertical distance h below B. If the intial velocity of the ball is 20ms−1 and the horizontal distance between O and C is 10 m. Find the value of h.

View SolutionA body is projected with velocity 24 ms−1 making an angle 30° with the horizontal. The vertical component of its velocity after 2s is (g=10ms−1 )
View SolutionA ball is projected from a point in a horizontal plane with a velocity of 20 m/s at 30∘ with the horizontal. Coefficient of restitution is 0.8, then
View SolutionFrom the top of a tower, 80m high from the ground a stone is thrown in the horizontal direction with a velocity of 8ms1. The stone reaches the ground after a time t and falls at a distance of d from the foot of the tower. Assuming g=10ms2, the time t and distance d are given respectively by
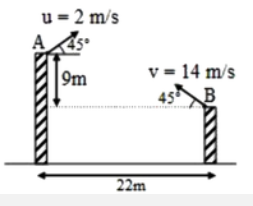
View SolutionTwo particles are simultaneously thrown from the top of two towards as shown. Their velocities are 2ms−1and14ms−1. Horizontal and vertical separations between these particles are 22 m and 9 m respectively. Then the minimum separation between the particles in the process of their motion in meters is (g=10ms−2)
View Solution