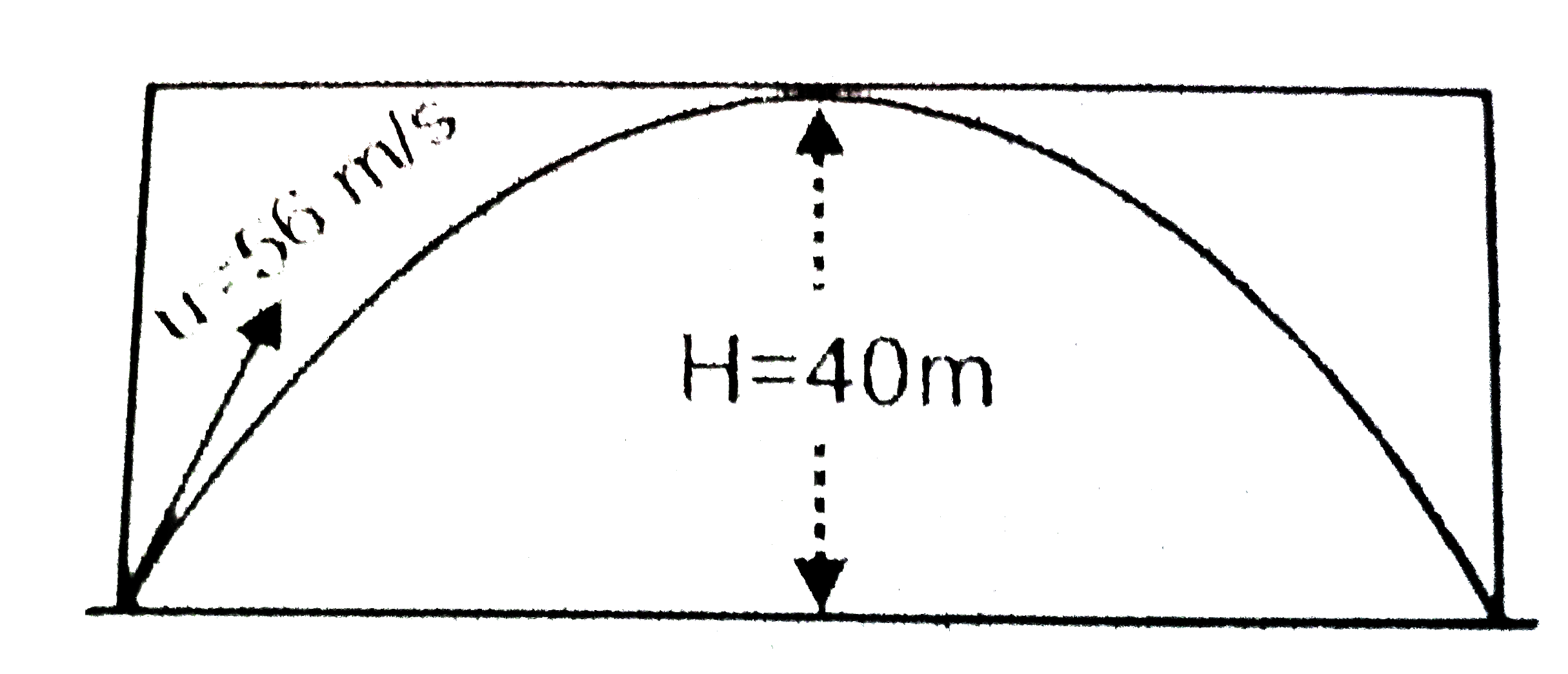
The ceiling of hall is 40 m high. For maximum horizontal distance, the angle at which the ball may be thrown with a speed of 56 m $s^{- 1}$ without hitting the ceiling of the ball is

A

$25^{\circ}$

B

$30^{\circ}$

C

$45^{\circ}$

D

$60^{\circ}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

$H = \frac{{(u sin θ)}^{2}}{2 g}$ $sin θ = \frac{\sqrt{2 g H}}{u} = \frac{\sqrt{2 \times 9.8 \times 40}}{56} = \frac{1}{2} \Rightarrow θ = 30^{\circ}$

|

Updated on:21/07/2023

Class 12 PHYSICS MOTION IN A PALNE

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The ceiling of a hall is 40m high. For maximum horizontal distance, the angle at which the ball may be thrown with a speed of $56 m s^{- 1}$ without hitting the ceiling of the hall is
A $25^{\circ}$
B $30^{\circ}$
C $45^{\circ}$
D $60^{\circ}$
Question 2 - Select One
In the question number 56, the maximum horizontal distance covered by the ball will be
A $160 \sqrt{3}$ m
B $140 \sqrt{3}$ m
C $120 \sqrt{3}$ m
D $100 \sqrt{3}$ m

ALLEN-MOTION IN A PALNE-EXERCISE-2

Home
Ask Doubt
Profile