A particle is projected an angle of 45∘ from 8m before the foot of a wall, just touches the top of the wall and falls on the ground on the opposite side at a distance 4m from it. The height of wall is:-
23m
43m
83m
34m
The correct Answer is:C
To solve the problem step by step, we can follow these instructions:
Step 1: Understand the Problem
A particle is projected at an angle of 45∘ from a point that is 8 meters away from the wall. It just touches the top of the wall and then lands 4 meters away from the wall on the opposite side. We need to find the height of the wall.
Step 2: Determine the Total Horizontal Range
The total horizontal distance covered by the projectile is the distance from the launch point to the wall plus the distance from the wall to the landing point.
- Distance to the wall = 8 m
- Distance from the wall to the landing point = 4 m
- Total horizontal range R=8+4=12 m
Step 3: Use the Projectile Motion Equation
For projectile motion, the vertical position y at a horizontal distance x can be expressed as:
y=xtanθ−gx22v2cos2θ
Where:
- y is the height at distance x
- θ is the angle of projection (45∘)
- g is the acceleration due to gravity (9.8m/s2)
- v is the initial velocity
- R is the total horizontal range
However, since we are only interested in the height of the wall when the projectile is at x=8 m, we can simplify our calculations using the known properties of projectile motion.
Step 4: Calculate the Height at x=8 m
Given that tan(45∘)=1, we can simplify our equation:
y=x−gx22v2
We need to express v2 in terms of R and g:
Using the range formula for projectile motion:
R=v2sin(2θ)g
For θ=45∘, sin(90∘)=1:
R=v2g⟹v2=gR
Substituting R=12 m:
v2=9.8×12=117.6m2/s2
Step 5: Substitute Back to Find Height
Now substitute v2 back into the height equation:
y=8−g⋅822⋅117.6
Calculating the second term:
y=8−9.8⋅64235.2
y=8−627.2235.2≈8−2.67≈5.33m
Step 6: Final Calculation
Thus, the height of the wall y is approximately 5.33 m.
Final Answer
The height of the wall is 83m or approximately 2.67m.
A particle is projected at an angle of 45∘ from a point that is 8 meters away from the wall. It just touches the top of the wall and then lands 4 meters away from the wall on the opposite side. We need to find the height of the wall.
The total horizontal distance covered by the projectile is the distance from the launch point to the wall plus the distance from the wall to the landing point.
- Distance to the wall = 8 m
- Distance from the wall to the landing point = 4 m
- Total horizontal range R=8+4=12 m
For projectile motion, the vertical position y at a horizontal distance x can be expressed as:
y=xtanθ−gx22v2cos2θ
Where:
- y is the height at distance x
- θ is the angle of projection (45∘)
- g is the acceleration due to gravity (9.8m/s2)
- v is the initial velocity
- R is the total horizontal range
Given that tan(45∘)=1, we can simplify our equation:
y=x−gx22v2
Using the range formula for projectile motion:
R=v2sin(2θ)g
For θ=45∘, sin(90∘)=1:
R=v2g⟹v2=gR
v2=9.8×12=117.6m2/s2
Now substitute v2 back into the height equation:
y=8−g⋅822⋅117.6
Calculating the second term:
y=8−9.8⋅64235.2
y=8−627.2235.2≈8−2.67≈5.33m
Thus, the height of the wall y is approximately 5.33 m.
The height of the wall is 83m or approximately 2.67m.
Topper's Solved these Questions
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - EXERCISE-3
40 Videos
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - SOLVED EXAMPLE
28 Videos
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - EXERCISE-1
99 Videos
- KINEMATICS-2DBOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)
46 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (JA)
4 Videos
Similar Questions
From a point on the ground at a distance a from the foot of a pole, a ball is thrown at an angle of 45∘, which just touches the top of the pole and strikes the ground at a distance of b, on the outer side of it. Find the height of the pole.
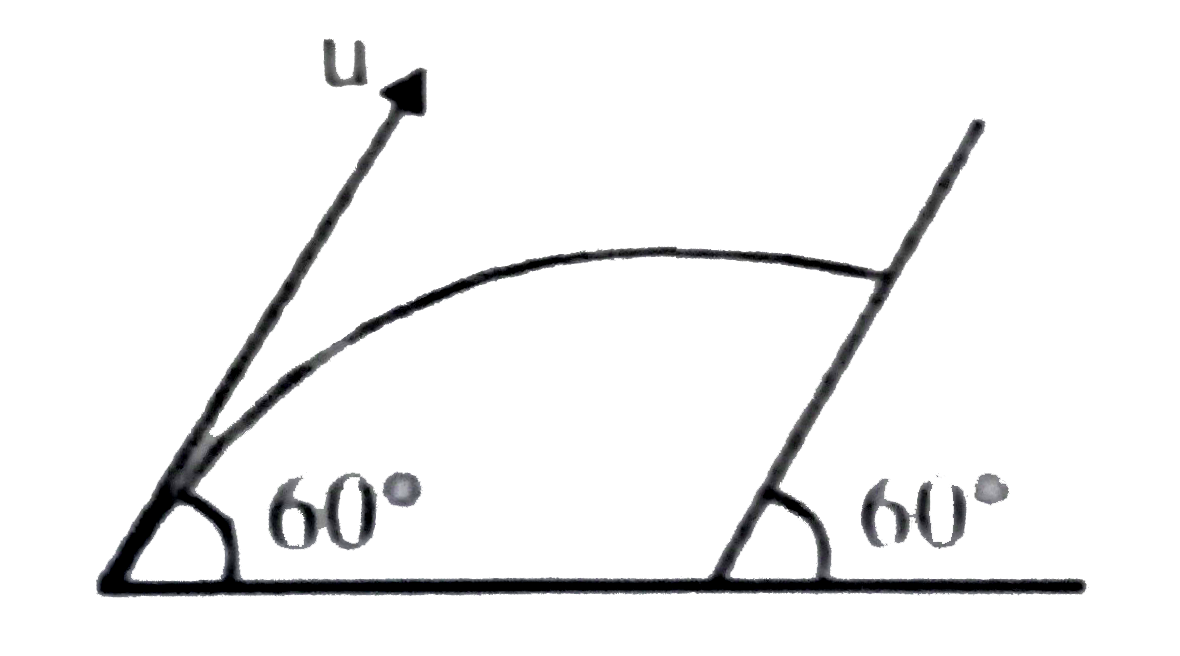
View SolutionA particle is projected at an angle 60∘ from Horizon from ground with speed u. after some time it collides with a wall inclined at an angle 30∘ from horizon. At the time of collision velocity of particle is perpendicular to the wall. Find speed of the particle at the time of collision :-
View Solution
Knowledge Check
The angle of elevation of the top of a tower. from a point on the ground and at a distance of 160 m from its foot, is find to be 60∘ . Find the height of the tower .
A277.12 mB377.12 mC477.12 mDNoneA body of mass m thrown horizontally with velocity v, from the top of tower of height h touches the level ground at a distance of 250m from the foot of the tower. A body of mass 2m thrown horizontally with velocity v/2, from the top of tower of height 4h will touch the level ground at a distance x from the foot of tower. The value of x is
A250 mB500 mC125 mD250√2 m
A particle is projected from the ground at t=0 so that on its way it just clears two vertical walls of equal height on the ground. The particle was projected with initial velocity u and at angle θ with the horiozontal. If the particle passes just grazing top of the wall at time t=t1andt=t2, then calculate.
(a) the height of the wall.
(b) the time t1andt2 in terms of height of the wall.
Write the expression for calculating the range of this projectile and separation between the walls.
View SolutionThe upper part of a tree, broken over by the wind. makes an angle of 45∘ with the ground , and the distance from the root to the point where the top of the tree touches the ground. is 1.5 m. What was the height of the tree before it was broken ?
View SolutionA particle projected at some angle with velocity 50 m/s crosses a 20 m high wall after 4 s from the time of projection. The angle of porjection of the particle is
View SolutionA ball is projected at t=0 with velocity v0 at angle θ with horizontal. It strikes a smooth wall at a distance from it and then falls at a distance d from the wall. Coefficient of restitution is 'e' then :
View SolutionA body of mass m thrown horizontally with velocity v, from the top of tower of height h touches the level ground at a distance of 250m from the foot of the tower. A body of mass 2m thrown horizontally with velocity v/2, from the top of tower of height 4h will touch the level ground at a distance x from the foot of tower. The value of x is
View SolutionA ladder 13 m long rests against a vertical wall. If the foot of the ladder is 5 m from the foot of the wall, find the distance of the other end of the ladder from the ground.
View Solution
