The retardation of a particle moving in a straight line is proportional to its displacement proportionallity constant being unity. Find the total distance convered by the particle till it comes to rest. Given that velocity of particle is v0 at zero displacement.
Uniform velocity
Uniform speed
Uniform acceleration
Data insufficient for generalization
The correct Answer is:D
To solve the problem, we need to find the total distance covered by a particle until it comes to rest, given that its retardation is proportional to its displacement. Let's break down the solution step by step.
Step 1: Understand the relationship between retardation and displacement
The problem states that the retardation (negative acceleration) of the particle is proportional to its displacement s. We can express this mathematically as:
a=−s
where a is the retardation.
Step 2: Relate acceleration to velocity and displacement
We know that acceleration can also be expressed in terms of velocity v and displacement s using the chain rule:
a=vdvds
Thus, we can set the two expressions for acceleration equal to each other:
vdvds=−s
Step 3: Rearranging the equation
Rearranging the equation gives us:
vdv=−sds
Step 4: Integrate both sides
Now, we will integrate both sides. The left side will be integrated with respect to v from the initial velocity v0 to 0 (when the particle comes to rest), and the right side will be integrated with respect to s from 0 to s0 (the total distance covered):
∫0v0vdv=−∫s00sds
Step 5: Perform the integration
The left side integrates to:
(v22)0v0=0−v202=−v202
The right side integrates to:
−(s22)s00=−s202
Step 6: Set the integrals equal to each other
Now we can set the results of the integrals equal to each other:
−v202=−s202
Step 7: Solve for s0
Multiplying through by -2 gives:
v20=s20
Taking the square root of both sides, we find:
s0=v0
Conclusion
The total distance covered by the particle until it comes to rest is:
v0
The problem states that the retardation (negative acceleration) of the particle is proportional to its displacement s. We can express this mathematically as:
a=−s
where a is the retardation.
We know that acceleration can also be expressed in terms of velocity v and displacement s using the chain rule:
a=vdvds
Thus, we can set the two expressions for acceleration equal to each other:
vdvds=−s
Rearranging the equation gives us:
vdv=−sds
Now, we will integrate both sides. The left side will be integrated with respect to v from the initial velocity v0 to 0 (when the particle comes to rest), and the right side will be integrated with respect to s from 0 to s0 (the total distance covered):
∫0v0vdv=−∫s00sds
The left side integrates to:
(v22)0v0=0−v202=−v202
The right side integrates to:
−(s22)s00=−s202
Now we can set the results of the integrals equal to each other:
−v202=−s202
Multiplying through by -2 gives:
v20=s20
Taking the square root of both sides, we find:
s0=v0
The total distance covered by the particle until it comes to rest is:
v0
Topper's Solved these Questions
- MOTION IN A PALNEBook:ALLENChapter:MOTION IN A PALNEExercise:EXERCISE-02
Explore 37 Videos
- MOTION IN A PALNEBook:ALLENChapter:MOTION IN A PALNEExercise:EXERCISE-03
Explore 6 Videos
- KINEMATICS-2DBook:ALLENChapter:KINEMATICS-2DExercise:Exercise (O-2)
Explore 46 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBook:ALLENChapter:NEWTON'S LAWS OF MOTION & FRICTIONExercise:EXERCISE (JA)
Explore 4 Videos
Similar Questions
If average velocity of particle moving on a straight line is zero in a time interval, then
View SolutionVelocity displacement graph of a particle moving in a straight line is as shown in figure.
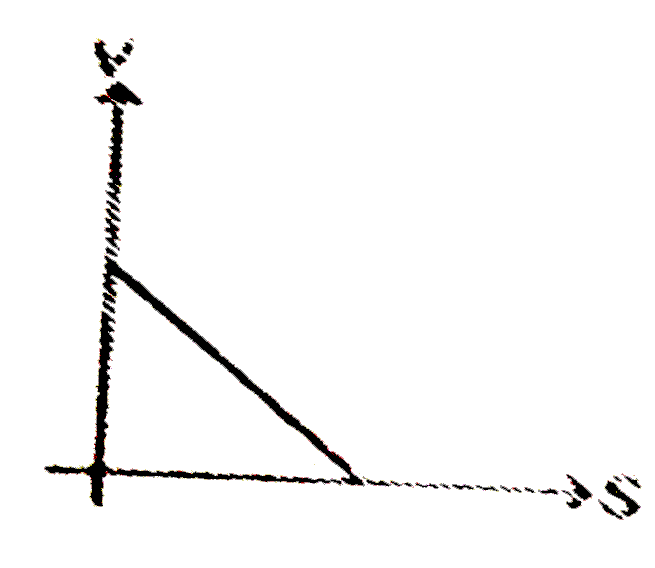
View SolutionDisplacement time graph of a particle moving in a straight line is a shown in figure.
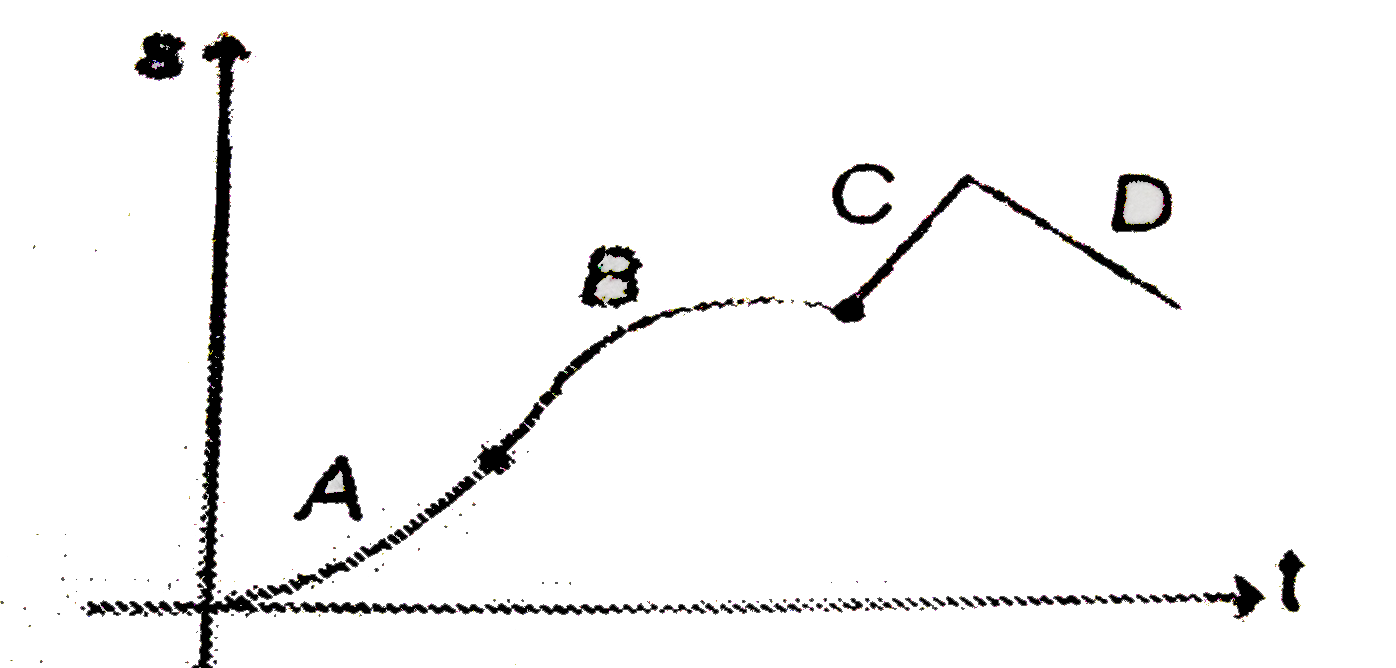
View SolutionA particle moves in a straight line with retardation proportional to its displacement. Its loss in kinetic energy for any displacement x is proportional to
View SolutionIf distance coverd by a particle is zero , what can be its displacement ?
View SolutionThe velocity-time graph of a particle moving in a staight line is shown in the . Find the displacement and the distance trav elled by the particle in 6s.
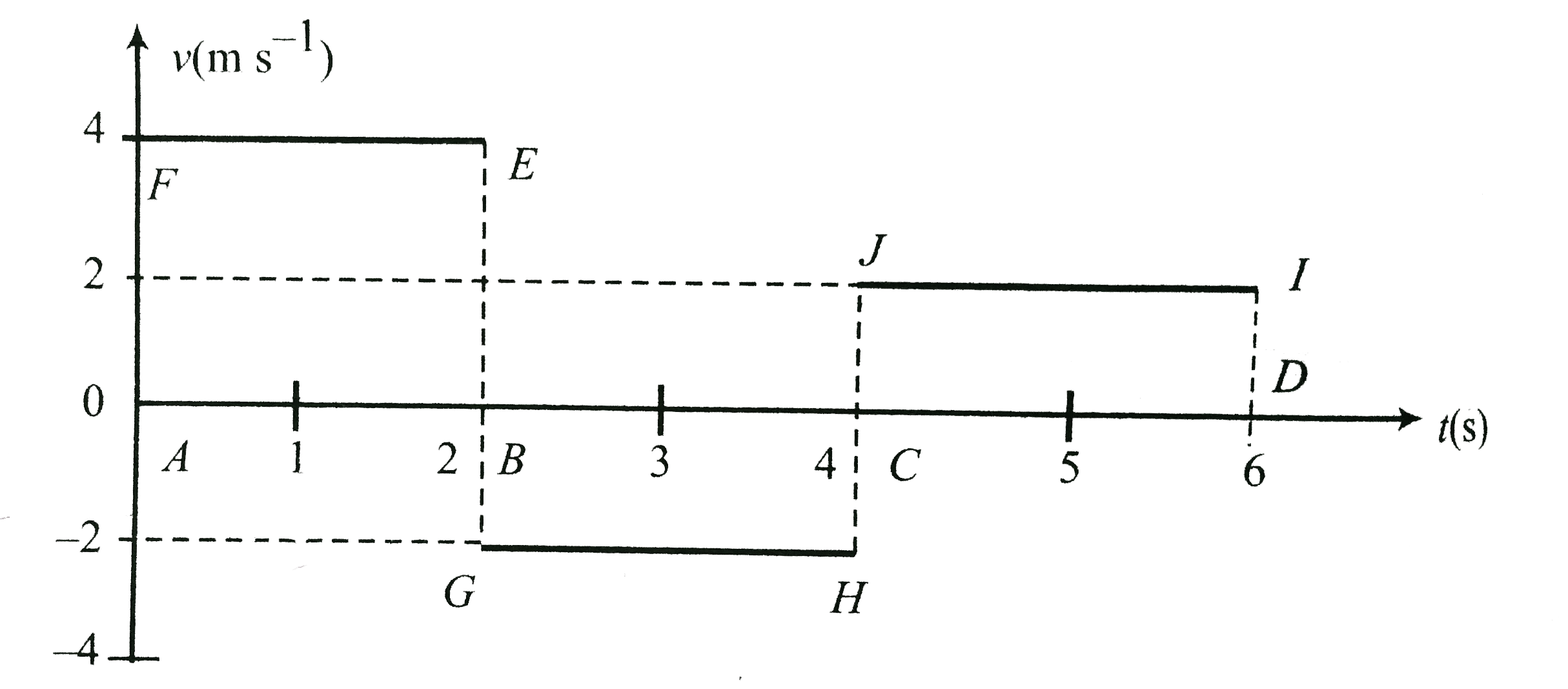 .
.
View SolutionThe acceleration of a particle moving in a straight line varies with its displacement as,a=2s+1 veocity o particle is zero at zero displacement. Find the corresponding velocity - displacement equation.
View SolutionAcceleration vs time graph is shown in the figure for a particle moving along a straight line. The particle is initially at rest. Find the time instant(s) when the particle comes to rest?
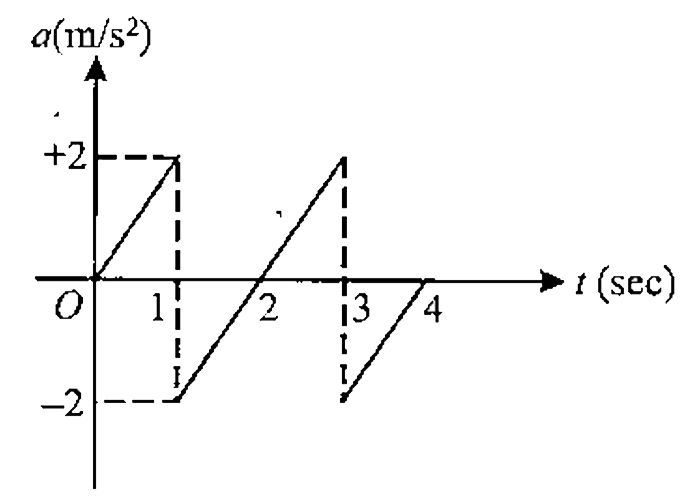
View SolutionA particle moves with an initial velocity V0 and retardation αv , where α is a constant and v is the velocity at any time t.
total distance covered by the particle is
View SolutionThe velocity of a particle moving in a straight line is directly proportional to 3/4th power of time elapsed. How does its displacement and acceleration depend on time?
View Solution

