The velocity of a particle moving in a straight line is directly proportional to power of time elapsed. How does its displacement and acceleration depend on time?
The correct Answer is:A, D
To solve the problem, we need to analyze how the velocity, displacement, and acceleration of a particle depend on time when the velocity is directly proportional to the 34 power of time elapsed.
1. Understanding the relationship of velocity with time:
Given that the velocity v is directly proportional to t34:
v=k⋅t34
where k is a constant of proportionality.
2. Finding acceleration:
Acceleration a is the derivative of velocity with respect to time:
a=dvdt
Now, differentiating v:
a=ddt(k⋅t34)=k⋅34t34−1=k⋅34t−14
Thus, we can express acceleration as:
a∝t−14
3. Finding displacement:
Displacement x is the integral of velocity with respect to time:
x=∫vdt=∫(k⋅t34)dt
Performing the integration:
x=k⋅∫t34dt=k⋅⎛⎝t34+134+1⎞⎠+C
Simplifying:
x=k⋅⎛⎝t7474⎞⎠+C=4k7t74+C
Ignoring the constant C for proportionality, we have:
x∝t74
Summary of Relationships:
- Velocity v∝t34
- Acceleration a∝t−14
- Displacement x∝t74
Given that the velocity v is directly proportional to t34:
v=k⋅t34
where k is a constant of proportionality.
Acceleration a is the derivative of velocity with respect to time:
a=dvdt
Now, differentiating v:
a=ddt(k⋅t34)=k⋅34t34−1=k⋅34t−14
Thus, we can express acceleration as:
a∝t−14
Displacement x is the integral of velocity with respect to time:
x=∫vdt=∫(k⋅t34)dt
Performing the integration:
x=k⋅∫t34dt=k⋅⎛⎝t34+134+1⎞⎠+C
Simplifying:
x=k⋅⎛⎝t7474⎞⎠+C=4k7t74+C
Ignoring the constant C for proportionality, we have:
x∝t74
- Velocity v∝t34
- Acceleration a∝t−14
- Displacement x∝t74
Topper's Solved these Questions
- KINEMATICSBook:DC PANDEY ENGLISHChapter:KINEMATICSExercise:Exercise 6.7
Explore 3 Videos
- KINEMATICSBook:DC PANDEY ENGLISHChapter:KINEMATICSExercise:Exercise 6.8
Explore 5 Videos
- KINEMATICSBook:DC PANDEY ENGLISHChapter:KINEMATICSExercise:Exercise 6.5
Explore 10 Videos
- GRAVITATIONBook:DC PANDEY ENGLISHChapter:GRAVITATIONExercise:(C) Chapter Exercises
Explore 45 Videos
- KINEMATICS 1Book:DC PANDEY ENGLISHChapter:KINEMATICS 1Exercise:INTEGER_TYPE
Explore 15 Videos
Similar Questions
The position of a particle moving on a straight line is proportional to the cube of the time elapsed. How does the acceleration of the particle depend on time elapsed?
View SolutionThe velocity time plot for a particle moving on straight line is shown in the figure.

View SolutionThe velocity time plot for a particle moving on straight line is shown in the figure.

View SolutionIf average velocity of particle moving on a straight line is zero in a time interval, then
View SolutionThe distance travelled by a particle in a straight line motion is directly proportional to t1/2, where t is the time elapsed.
View SolutionThe acceleration - velocity graph of a particle moving in a straight line is shown in figure. Then the slope of the velocity- displacement graph
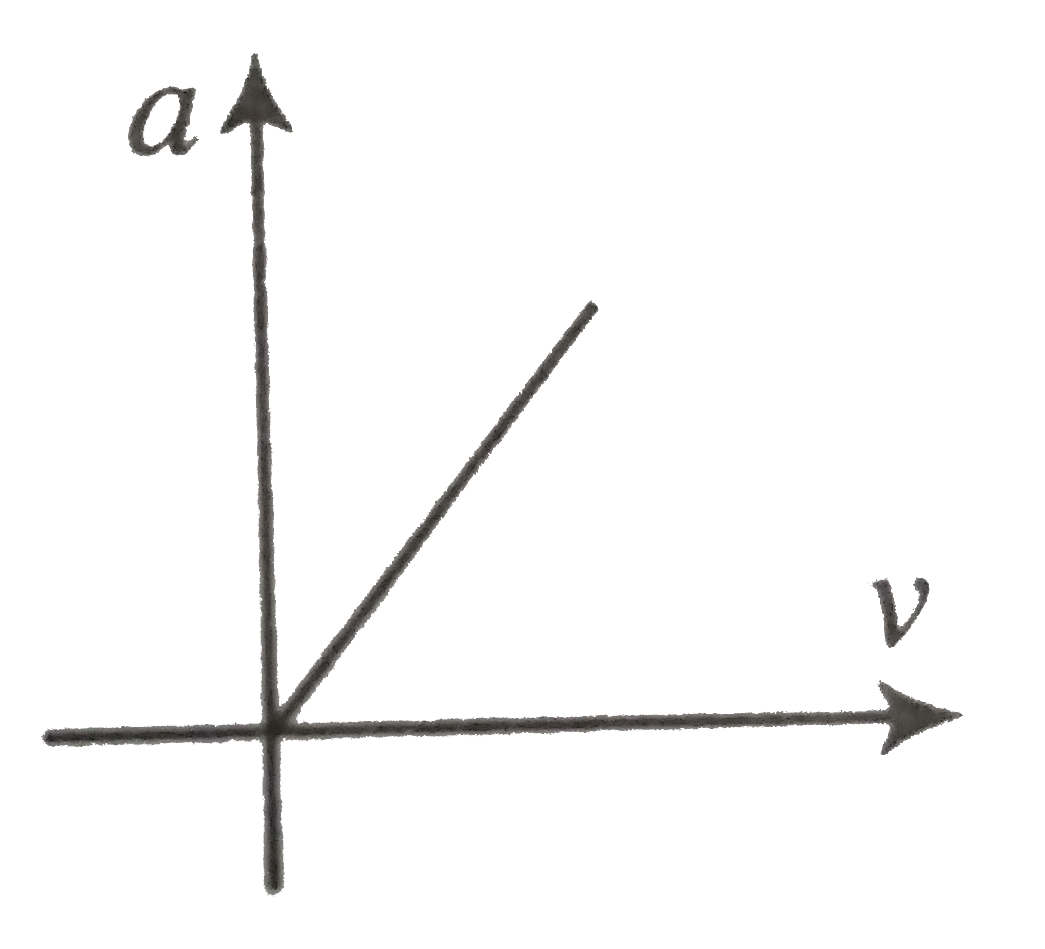
View SolutionKinetic energy of a particle moving in a straight line is proportional to the time t. The magnitude of the force acting on the particle is :
View SolutionVelocity displacement graph of a particle moving in a straight line is as shown in figure.
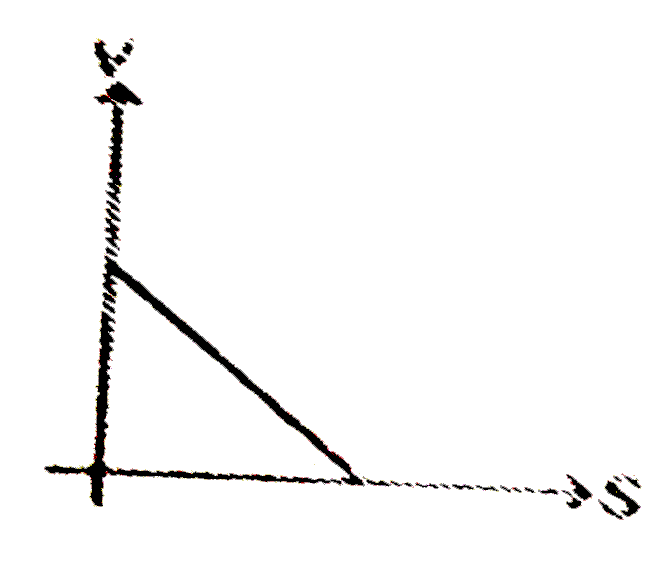
View SolutionThe velocity - time graph of a particle moving along a straight line is shown in the figure given below
The displacement of the particle in 5 second is
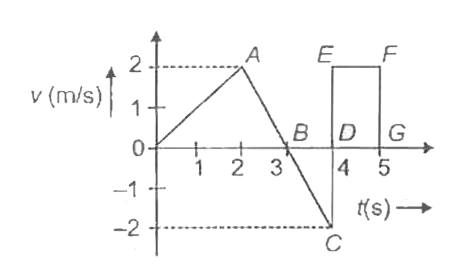
View SolutionDisplacement time graph of a particle moving in a straight line is a shown in figure.
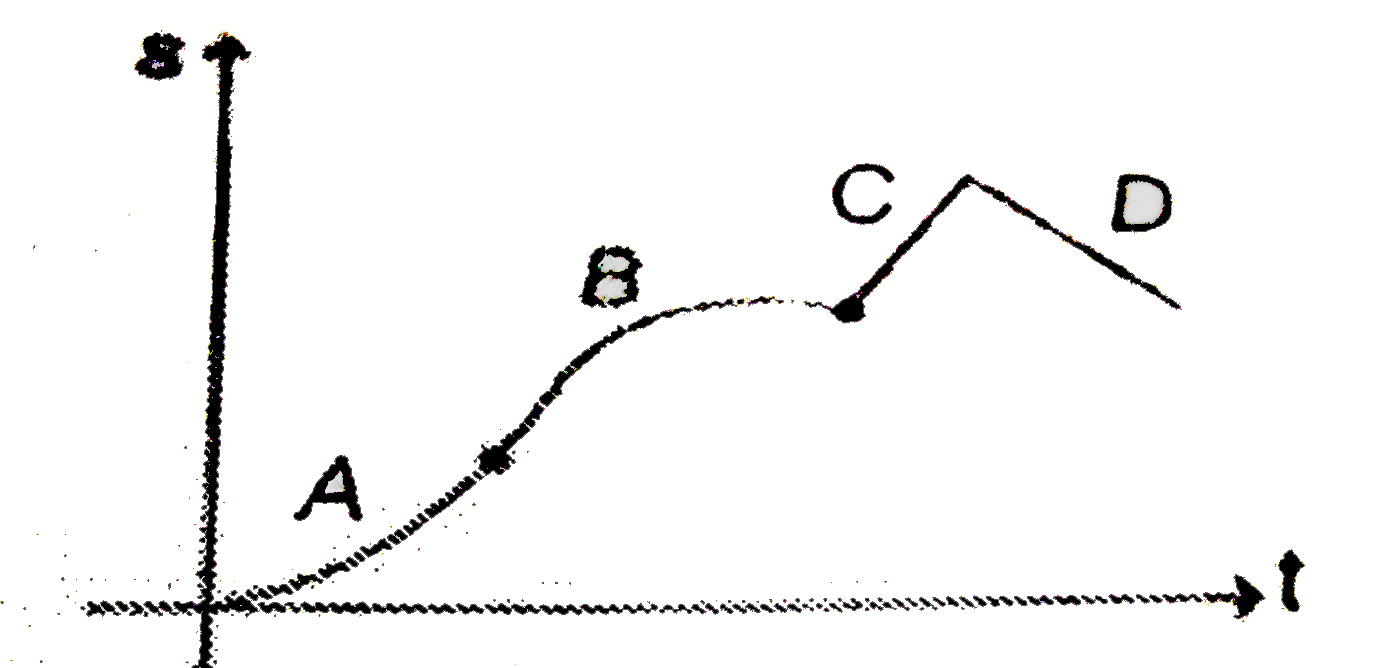
View Solution