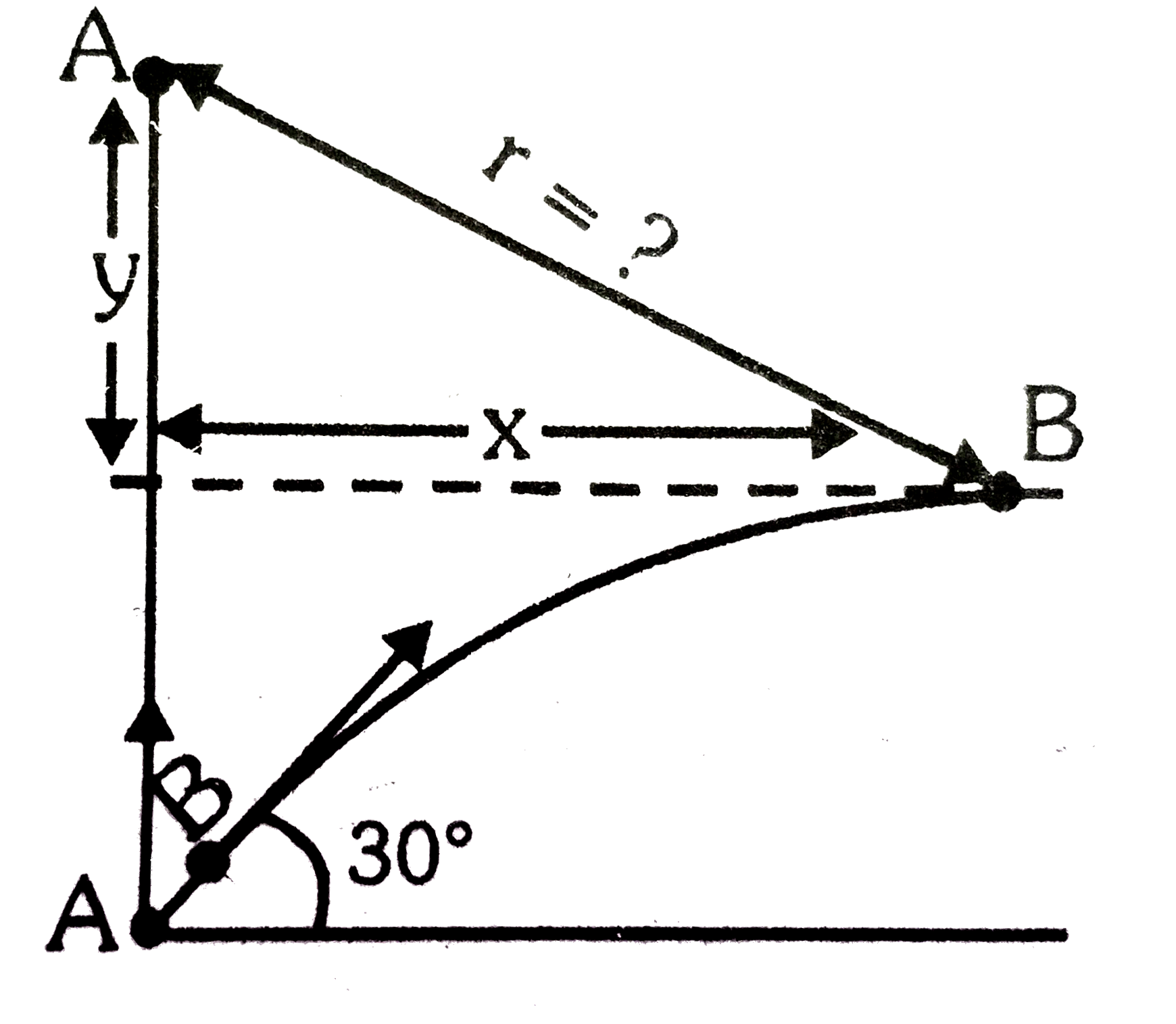
Two bodies were thrown simultaneously from the same point, one straight up, and the other at an angle of θ=30∘ to the horizontal. The initial velocity of each body is 20ms−1. Neglecting air resistance, the distance between the bodies at t=1.2 later is
y=(20×1.2−12gt2)−(20sin30∘×1.2−12gt2)=24−12=12m
x=20cos30∘×1.2=24×√32⇒12√3m
Distance between two bodies =√(12)2+(12√3)2=24m
Topper's Solved these Questions
Similar Questions
A body is thrown horizontally from the top of a tower of height 5m. It touches the ground at a distance of 10m from the foot of the tower. Find the initial velocity of the body.
View SolutionTwo bodies are thrown with the same initial velocity at angles θ and (90∘−θ) respectively with the horizontal, then their maximum height are in the ratio
View SolutionTwo bodies are thrown simultaneously from a tower with same initial velocity v0: one vertically upwards, the other vertically downwards. The distance between the two bodies after time t is
View SolutionTwo projectiles thrown from the same point at angles 60∘and30∘ with the horizontal attain the same height. The ratio of their initial velocities is
View SolutionA body is projected with a velocity 60ms−1at30∘ to horizontal . Its initial velocity vector is
View SolutionTwo bodies are thrown with the same initial velocity of 30 m/s. One at 17°, other at 73° to the horizontal. The sum of the maximum heights reached by them is [g = 10 m/s2]
View SolutionA body is projected down from height of 60 m with a velocity 10ms−1 at angle 30∘ to horizontal. The time of flight of the body is [g=10ms−2]
View SolutionA body is projected with an initial Velocity 20 m/s at 60° to the horizontal. Its velocity after 1 sec is
View SolutionA body is projected at angle 30° to the horizontal with a velocity 50ms−1 maximum height of projectile is
View SolutionA body is project at t= 0 with a velocity 10ms−1 at an angle of 60∘ with the horizontal .The radius of curvature of its trajectory at t=1s is R. Neglecting air resitance and taking acceleration due to gravity g=10ms−2, the value of R is :
View Solution
