A rod with rectangular cross section oscillates about a horizontal axis passing through one of its ends and it behaves like a seconds pendulum, its length will be
To find the length of a rod with a rectangular cross-section that behaves like a seconds pendulum when oscillating about a horizontal axis passing through one of its ends, we can follow these steps:
Step 1: Understand the Time Period Formula
The time period T for a rigid body oscillating about a pivot is given by the formula:
T=2π√Imgd
where:
- I is the moment of inertia of the rod,
- m is the mass of the rod,
- g is the acceleration due to gravity,
- d is the distance from the pivot to the center of mass.
Step 2: Calculate the Moment of Inertia
For a rod of length L and mass m, the moment of inertia about its center is:
Icm=mL212
Using the parallel axis theorem, the moment of inertia about the end of the rod is:
I=Icm+md2=mL212+m(L2)2
Calculating d2:
d=L2⟹d2=(L2)2=L24
Thus, we have:
I=mL212+mL24=mL212+3mL212=4mL212=mL23
Step 3: Substitute into the Time Period Formula
Substituting I back into the time period formula:
T=2π
⎷mL23mgL2
Simplifying this expression:
T=2π√L23g⋅2L=2π√2L3g
Step 4: Set the Time Period Equal to That of a Seconds Pendulum
The time period for a seconds pendulum is:
T=2π√Lpg
where Lp is the length of the seconds pendulum, which is 1m.
Setting the two time periods equal:
2π√2L3g=2π√Lpg
Squaring both sides and simplifying:
2L3g=Lpg
Cancelling g from both sides:
2L3=Lp
Substituting Lp=1m:
2L3=1⟹2L=3⟹L=32m=1.5m
Final Answer
The length of the rod that behaves like a seconds pendulum is:
L=1.5m
The time period T for a rigid body oscillating about a pivot is given by the formula:
T=2π√Imgd
where:
- I is the moment of inertia of the rod,
- m is the mass of the rod,
- g is the acceleration due to gravity,
- d is the distance from the pivot to the center of mass.
For a rod of length L and mass m, the moment of inertia about its center is:
Icm=mL212
Using the parallel axis theorem, the moment of inertia about the end of the rod is:
I=Icm+md2=mL212+m(L2)2
Calculating d2:
d=L2⟹d2=(L2)2=L24
Thus, we have:
I=mL212+mL24=mL212+3mL212=4mL212=mL23
Substituting I back into the time period formula:
T=2π
⎷mL23mgL2
Simplifying this expression:
T=2π√L23g⋅2L=2π√2L3g
The time period for a seconds pendulum is:
T=2π√Lpg
where Lp is the length of the seconds pendulum, which is 1m.
2π√2L3g=2π√Lpg
Squaring both sides and simplifying:
2L3g=Lpg
Cancelling g from both sides:
2L3=Lp
Substituting Lp=1m:
2L3=1⟹2L=3⟹L=32m=1.5m
The length of the rod that behaves like a seconds pendulum is:
L=1.5m
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - SOME WORKED OUT EXAMPLES
29 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-01
117 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
24 Videos
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
Similar Questions
A thin uniform rod of mass M and length L is free to rotate in vertical plane about a horizontal axis passing through one of its ends. The rod is released from horizontal position shown in the figure. Calculate the shear stress developed at the centre of the rod immediately after it is released. Cross sectional area of the rod is A. [For calculation of moment of inertia you can treat it to very thin]

View SolutionA thin uniform copper rod length l and mass m rotates unifomly with an angular velocity ω about a vertical axis passing through one of its ends as shown in the figure. Young's modulus of copper is Y. Breaking stress is σmax, cross sectional area of rod is A and density of rod is uniform. Based on above information, answer the following questions
The maximum angular velocity with which the rod can rotate so that is won't break, is

View Solution
Knowledge Check
A uniform rod of mass m. length L, area of cross- secticn A is rotated about an axis passing through one of its ends and perpendicular to its length with constant angular velocity omega in a horizontal plane If Y is the Young's modulus of the material of rod, the increase in its length due to rotation of rod is
Amω2L2AYBmω2L22AYCmω2L23AYD2mω2L2AYThe radius of gyration of an uniform rod of length l about an axis passing through one of its ends and perpendicular to its length is.
Al√2Bl3Cl√3Dl2

A uniform rod of length 4l and mass m is free to rotate about a horizontal axis passing through a point distant l from its one end. When the rod is horizontal its angular velocity is ω as shown in figure. calculate
(a). reaction of axis at this instant,
(b). Acceleration of centre of mass of the rod at this instant.
(c). reaction of axis and acceleration of centre mass of the rod when rod becomes vertical for the first time.
(d). minimum value of ω, so that centre of rod can complete circular motion.
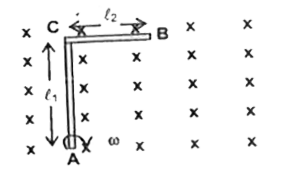
View SolutionFor an L shaped conducting rod placed in an uniform magnetic field →B rotating with constant angular velocity ω about an axis passing through one of its ends A and normal to the plane of the conductor induced emf
View SolutionA uniform rod of length l oscillates about an axis passing through its end. Find the oscillation period and the reduced length of this pendulum.
View Solutionfind the radius of gyration of a rod of mass m and length 2l about an axis passing through one of its ends and perpendicular to its length.
View SolutionA thin uniform copper rod of length l and mass m rotates uniformly with an angular velocity ω in a horizontal plane about a vertical axis passing through one of its ends. Determine the tension in the rod as a function of the distance r from the rotation axis. Find the elongation of the rod.
View SolutionThe moment of inertia of a thin uniform rod of mass M and length L about an axis passing through its mid-point and perpendicular to its length isI0. Its moment of inertia about an axis passing through one of its ends perpendicular to its length is.
View Solution
