A rectangulat block of refractive index μ is placed on a printed page lying on a horizontal surface as shown in Fig. , Find the minimum value of μ so that the letter L on the page is not visible from any of the vertical sides.
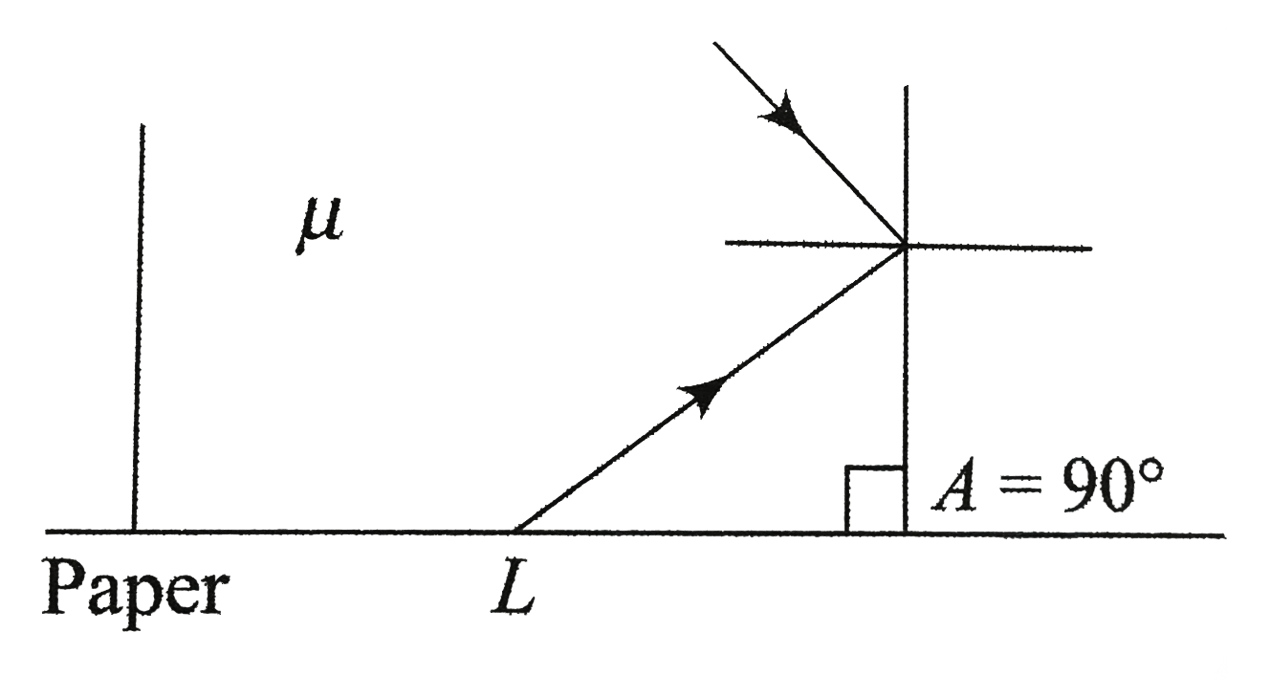
The situation is depicted in figure. Light will not emerge out from the vertical face BC if at it I>θCorsinI>sinθC⇒sinI>1μ[assinθC=1μ]…(i)
But from Snell's law at O1×sinθ=μsinr
And in ΔOPR,r+90+i=180⇒r+i=90∘⇒r=90−i
_S01_011_S01.png)
So sinθ=μsin(90−i)=μcosi⇒cosi=sinθμ
so sini=√1−cos2i=√1−[sinθμ]2....(ii)
so substituting the value of sin i from equation (ii) in (i),
√1−sin2θμ2>1μ i.e., μ2>1+sin2θ
∵(sin2θ)max=1∴μ2>2√2∴μmin=√2
Topper's Solved these Questions
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:SOME WORKED OUT EXAMPLES
Explore 83 Videos
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:EXERCISE -01
Explore 65 Videos
- CURRENT ELECTRICITYBook:ALLENChapter:CURRENT ELECTRICITYExercise:EX.II
Explore 66 Videos
- GRAVITATIONBook:ALLENChapter:GRAVITATIONExercise:EXERCISE 4
Explore 9 Videos
Similar Questions
In the figure shown, μ1>μ2. Find minimum value of i so that TIR never takes place at P.

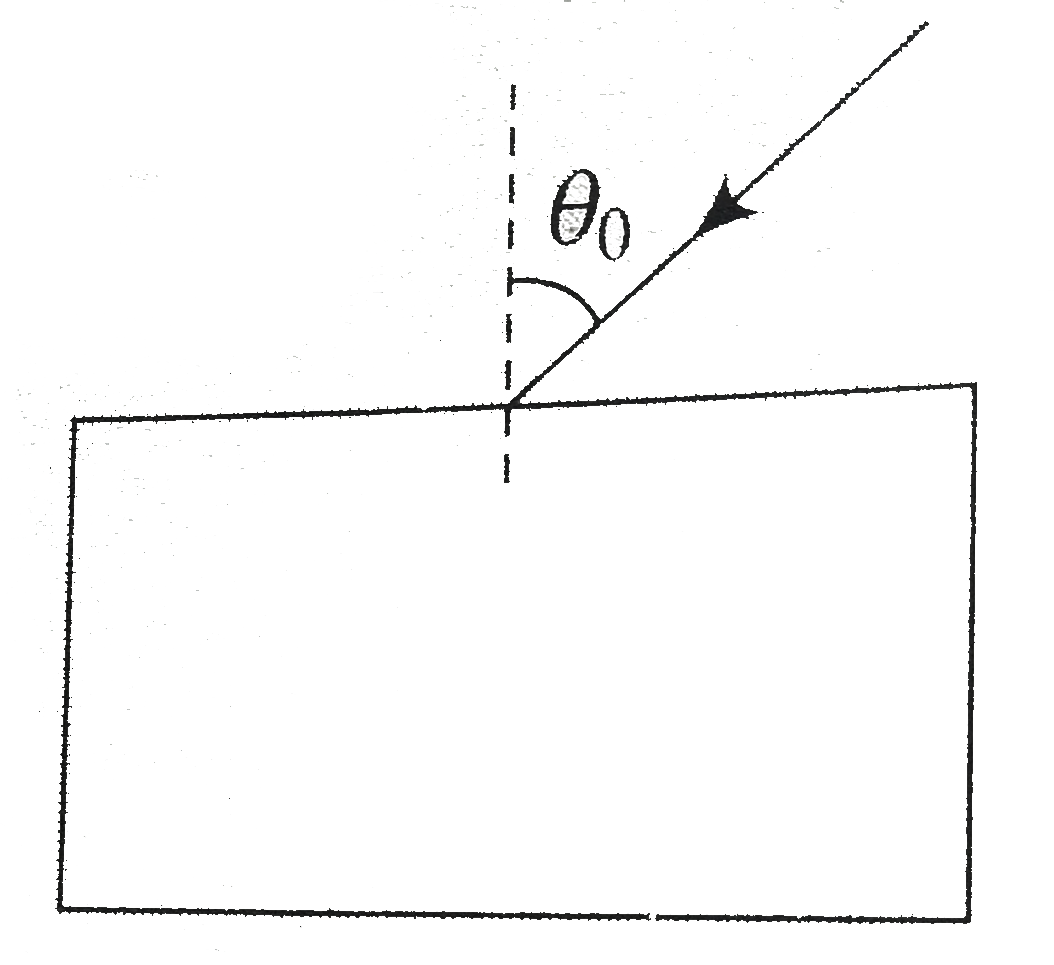
View SolutionA slab of refractive index μ is placed in air and light is incident at maximum angle θ0 from vertical. Find minimum value of μ for which total internal reflection takes place at the vertical surface.
View SolutionA cubical transparent slab is used as a paper weight. What should be the minimum refractive index of the material of the slab so that letters below it are not visible from any of its vertical faces.
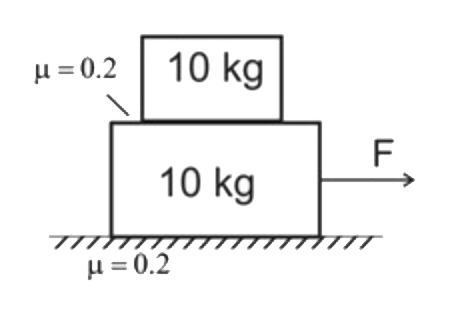
View SolutionInitially, both the blocks are at rest on horizontal surface as shown in the figure. Find the minimum value of force F in (N) so that sliding starts between the blocks (g=10ms−2)
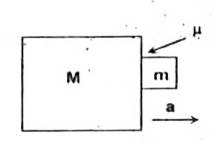
View SolutionA body of mass M is moving in +x-direction with acceleration a. Find the minimum value of μ so that a body of mass m can be held stationary with respect to M, on the vertical side of M.
View SolutionA jar of height h is filled wih a transparent liquid of refractive index μ, Fig. At the centre of the jar on the botom surface is a dot. Find the minimum diameter of a disc, such that when placed on the top surface symmetrically about the centre, the dot is invisible.
 .
.
View SolutionA block of mass m is placed on another block of mass M lying on a smooth horizontal surface as shown in the figure. The co-efficient of friction between the blocks is μ. Find the maximum horizontal force F (in Newton) that can be applied to the block M so that the blocks together with same acceleration? (M=3kg,m=2kg,μ=0.1,g=10m/s2)

View SolutionTwo blocks of masses 1 kg and 2 kg are placed in contact on a smooth horizontal surface as shown in fig. A horizontal force of 6N is applied d(a) on a 1-kg block. Find the force of interaction of the blocks.

 .
.
View SolutionThe figure an L shaped body of mass M placed on smooth horizontal surface. The block A is connected to the body by means of an inexiensible string , which is passing over a smooth pulley of negligible mass.Another block B of mass m is placed against a vertical wall of the body. Find the minimum value of the mass of block A so that B remain stationary relative to the wall. Coefficient of friction between the block B and the vertical wall is μ.

View SolutionThe convex surface of a thin concave-convex lens of glass of refractive index 1.5 has a radius of curvature 20 cm. The concave surface has a radius of curvature 60 cm. The convex side is silvered and placed on a horizontal surface as shown in figure. (a) Where should a pin be placed on the axis so that its image is formed at the same place ? (b) If the concave part is filled with water (mu = 4/3), find the distance through which the pin should be moved so that the image of the pin again coincides with the pin.

View Solution