The figure an L shaped body of mass M placed on smooth horizontal surface. The block A is connected to the body by means of an inexiensible string , which is passing over a smooth pulley of negligible mass.Another block B of mass m is placed against a vertical wall of the body. Find the minimum value of the mass of block A so that B remain stationary relative to the wall. Coefficient of friction between the block B and the vertical wall is μ.
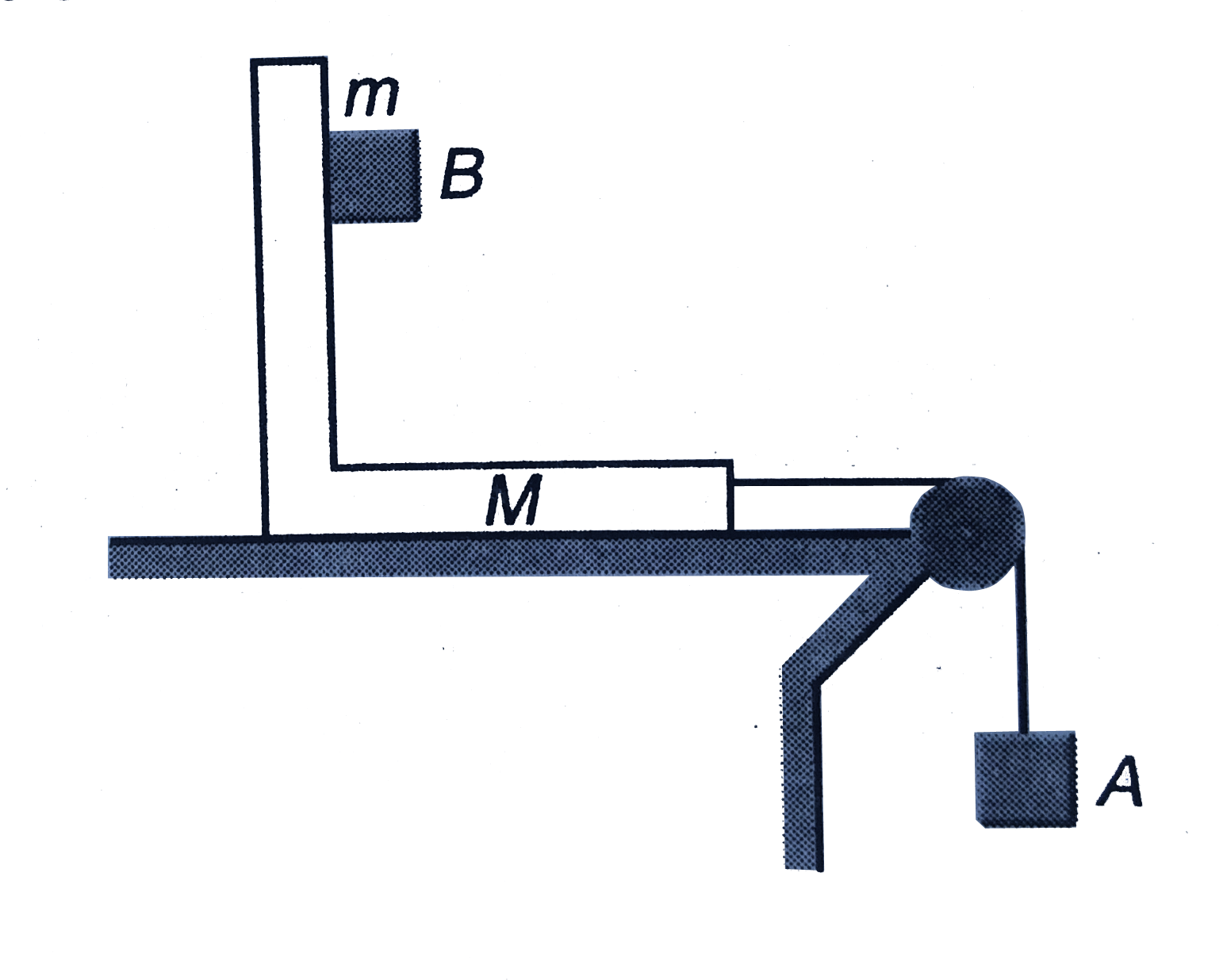
a=mAgmA+M+m
For the equilibrium of B
mg=μN=μ(ma)=μmmAgmA+M+m
∴mA=(M+m)m(μ−1)m
mA=(M+m)μ−1
Topper's Solved these Questions
- LAWS OF MOTIONBook:DC PANDEY ENGLISHChapter:LAWS OF MOTIONExercise:Check point 5.1
Explore 20 Videos
- LAWS OF MOTIONBook:DC PANDEY ENGLISHChapter:LAWS OF MOTIONExercise:Check point 5.2
Explore 15 Videos
- LAWS OF MOTIONBook:DC PANDEY ENGLISHChapter:LAWS OF MOTIONExercise:Comprehension
Explore 9 Videos
- KINEMATICS 1Book:DC PANDEY ENGLISHChapter:KINEMATICS 1Exercise:INTEGER_TYPE
Explore 15 Videos
- LAWS OF THERMODYNAMICSBook:DC PANDEY ENGLISHChapter:LAWS OF THERMODYNAMICSExercise:Level 2 Subjective
Explore 18 Videos
Similar Questions
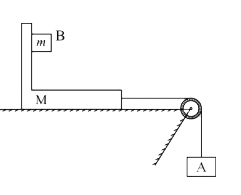
In the given situation, what is the minimum mass of block A so that block B remains stationary with respect to the wall? The coefficient of friction is μ between wall and block. All other surfaces are smooth.
View SolutionA block of mass M is placed on a rough horizontal surface. It is connected by means of a light inextensible string passing over a smooth pulley . The other end of string is connected to a block of mass m. There is no friction between vertical surface and block m
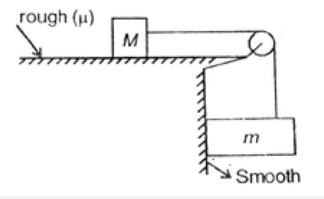
The minimum value of coefficient of friction μ such that system remains at rest , is
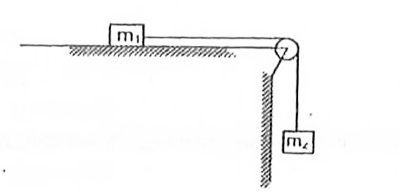
View SolutionA block of mass m1=2 kg is kept on a smooth horizontal table. Another block of mass m2=1 kg is connected to m1 by a light inextensible string passing over a smooth pulley as shown in the figure. If the blocks are released, what will be the (a) acceleration of each block (b) tension in the string?
View SolutionA block of mass M is placed on a rough horizontal surface. It is connected by means of a light inextensible string passing over a smooth pulley . The other end of string passing over a smooth pulley. The other end of string is connected to a block of mass m. There is no friction between vertical surface and block m

If the coefficient of friction of friction μ is less than the above value, then downward acceleration of block m is
View SolutionIn the arrangement shown in the figure, mass of the block B and A is 2m and m respectively. Surface between B and floor is smooth. The block B is connected to the block C by means of a string-pulley system. If the whole system is released, then find the minimum value of mass of block C so that A remains stationary w.e.t. B. Coefficient of friction between A and B is μ.

View SolutionA light string passing over a smooth light pulley connects two blocks of masses m1 and m2 (vertically). If the acceleration of the system is g/8, then the ratio of the masses is
View SolutionA light string passing over a smooth light pulley connects two blocks of masses m1 and m2 (vertically). If the acceleration of the system is g/8, then the ratio of the masses is
View SolutionA block of mass M placed on a frictionless horizontal table is pulled by another block of mass m hanging vertically by a massless string passing over a frictionless pulley. The tension in the string is :
View SolutionA block of mass m is attached at the end of an inextensible string which is wound over a rough pulley of mass M and radius R figure a. Assume the string does not slide over the pulley. Find the acceleration of the block when released.
View SolutionA block of mass M is placed on a rough horizontal surface. It is connected by means of a light inextensible string passing over a smooth pulley . The other end of string passing over a smooth pulley. The other end of string is connected to a block of mass m. There is no friction between vertical surface and block m
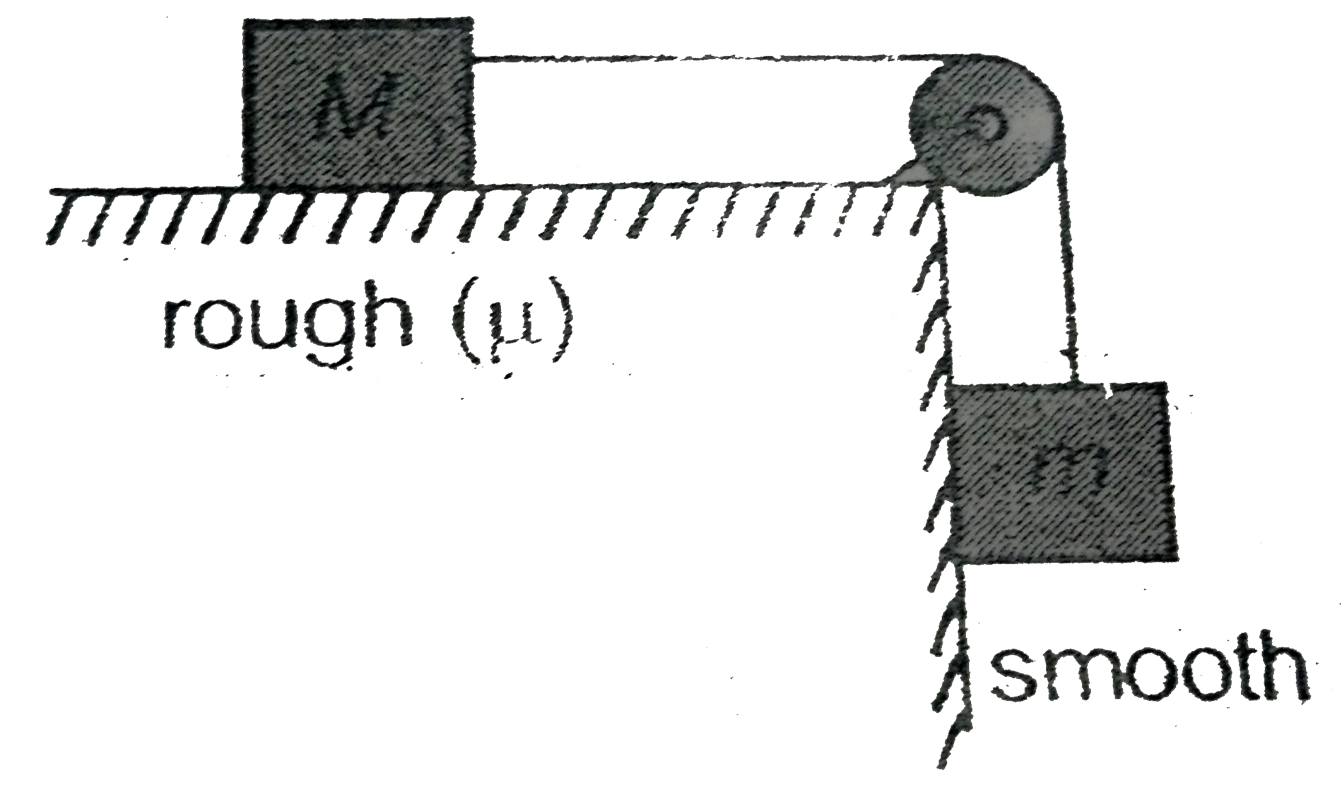
If the whole system ( horizontal surface + blocks ) accelerates towards right the value of maximum on the horizontal surface is
View Solution