A light string passing over a smooth light pulley connects two blocks of masses and (vertically). If the acceleration of the system is , then the ratio of the masses is
(a)
(b)
(c)
(d)
The correct Answer is:B
To solve the problem of finding the ratio of the masses m1 and m2 when the acceleration of the system is g8, we can follow these steps:
Step 1: Draw Free Body Diagrams
We start by drawing the free body diagrams for both masses m1 and m2.
- For mass m1:
- The forces acting on it are the gravitational force m1g acting downward and the tension T acting upward.
- For mass m2:
- The forces acting on it are the gravitational force m2g acting downward and the tension T acting upward.
Step 2: Write the Equations of Motion
Using Newton's second law, we can write the equations of motion for both masses.
1. For mass m1:
T−m1g=−m1a(1)
Here, a is the acceleration of the system, which is g8.
2. For mass m2:
m2g−T=m2a(2)
Step 3: Substitute the Acceleration
Substituting a=g8 into both equations:
1. From equation (1):
T−m1g=−m1(g8)
Rearranging gives:
T=m1g−m1g8=m1g(1−18)=m1g(78)(3)
2. From equation (2):
m2g−T=m2(g8)
Rearranging gives:
T=m2g−m2g8=m2g(1−18)=m2g(78)(4)
Step 4: Equate the Tensions
From equations (3) and (4), we can set the expressions for T equal to each other:
m1g(78)=m2g(78)
Since g and 78 are common on both sides, we can simplify:
m1=m2
Step 5: Find the Ratio of the Masses
To find the ratio of the masses, we can express it as:
m2m1=m1m1=1
Final Result
Thus, the ratio of the masses m2m1 is:
m2m1=97
We start by drawing the free body diagrams for both masses m1 and m2.
- The forces acting on it are the gravitational force m1g acting downward and the tension T acting upward.
- For mass m2:
- The forces acting on it are the gravitational force m2g acting downward and the tension T acting upward.
Using Newton's second law, we can write the equations of motion for both masses.
T−m1g=−m1a(1)
Here, a is the acceleration of the system, which is g8.
m2g−T=m2a(2)
Substituting a=g8 into both equations:
T−m1g=−m1(g8)
Rearranging gives:
T=m1g−m1g8=m1g(1−18)=m1g(78)(3)
m2g−T=m2(g8)
Rearranging gives:
T=m2g−m2g8=m2g(1−18)=m2g(78)(4)
From equations (3) and (4), we can set the expressions for T equal to each other:
m1g(78)=m2g(78)
Since g and 78 are common on both sides, we can simplify:
m1=m2
To find the ratio of the masses, we can express it as:
m2m1=m1m1=1
Thus, the ratio of the masses m2m1 is:
m2m1=97
Topper's Solved these Questions
- DYNAMICS OF A PARTICLEBook:VMC MODULES ENGLISHChapter:DYNAMICS OF A PARTICLEExercise:JEE Advance (Archive) Level - II (SINGLE OPTION CORRECT TYPE )
Explore 31 Videos
- DYNAMICS OF A PARTICLEBook:VMC MODULES ENGLISHChapter:DYNAMICS OF A PARTICLEExercise:LEVEL 2 ( NUMERICAL TYPE FOR JEE MAIN )
Explore 16 Videos
- DC CIRCUITBook:VMC MODULES ENGLISHChapter:DC CIRCUITExercise:JEE ADVANCED ARCHIVE
Explore 68 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBook:VMC MODULES ENGLISHChapter:ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTExercise:IN-CHAPTER EXERCISE-G
Explore 10 Videos
Similar Questions
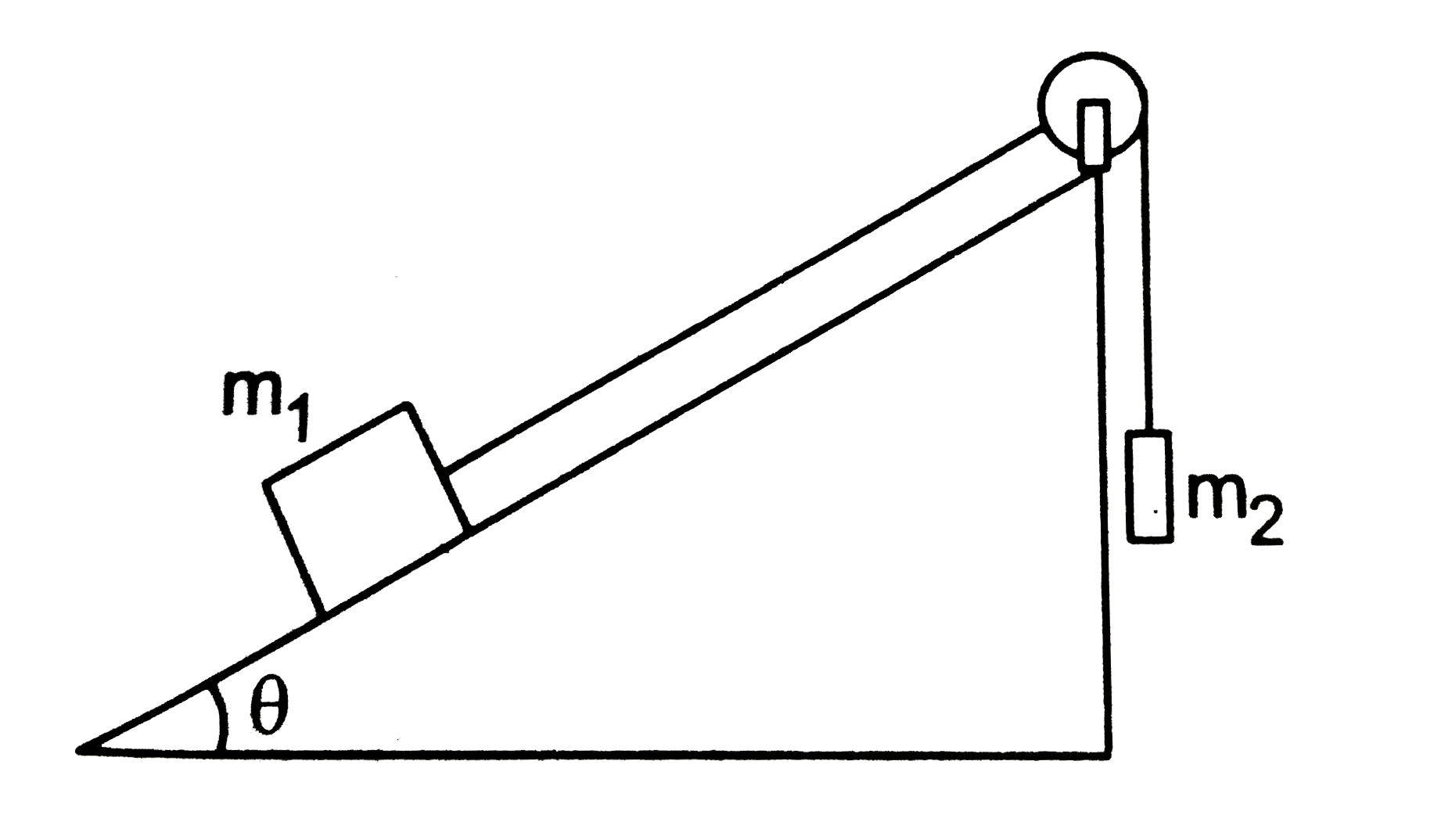
Two bodies of masses m1andm2 are connected by a light string going over a smooth lilght pulley at the end of an incline. The mass1 lies on the incline m2 hangs vertically. The system is t rest. Find the angle of the incline and the fore exerted by the incline on the body of mass m_1.
View SolutionTwo bodies of masses 1 kg and 2 kg are connected by a very light string passed over a clamped light smooth pulley. If the system is released from rest, find the acceleration of the two masses and the tension in the string
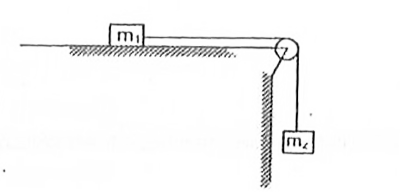
View SolutionA block of mass m1=2 kg is kept on a smooth horizontal table. Another block of mass m2=1 kg is connected to m1 by a light inextensible string passing over a smooth pulley as shown in the figure. If the blocks are released, what will be the (a) acceleration of each block (b) tension in the string?
View SolutionTwo masses 2 kg and 4 kg are connected at the two ends of light inextensible string passing over a frictionless pulley. If the masses are released, then find the acceleration of the masses and the tension in the string.
View SolutionTwo masses 2 kg and 4 kg are connected at two ends of light inextensible string passing over a frictionless pulley . If the masses are released , then find the accelaration of the masses and the tension in the string .
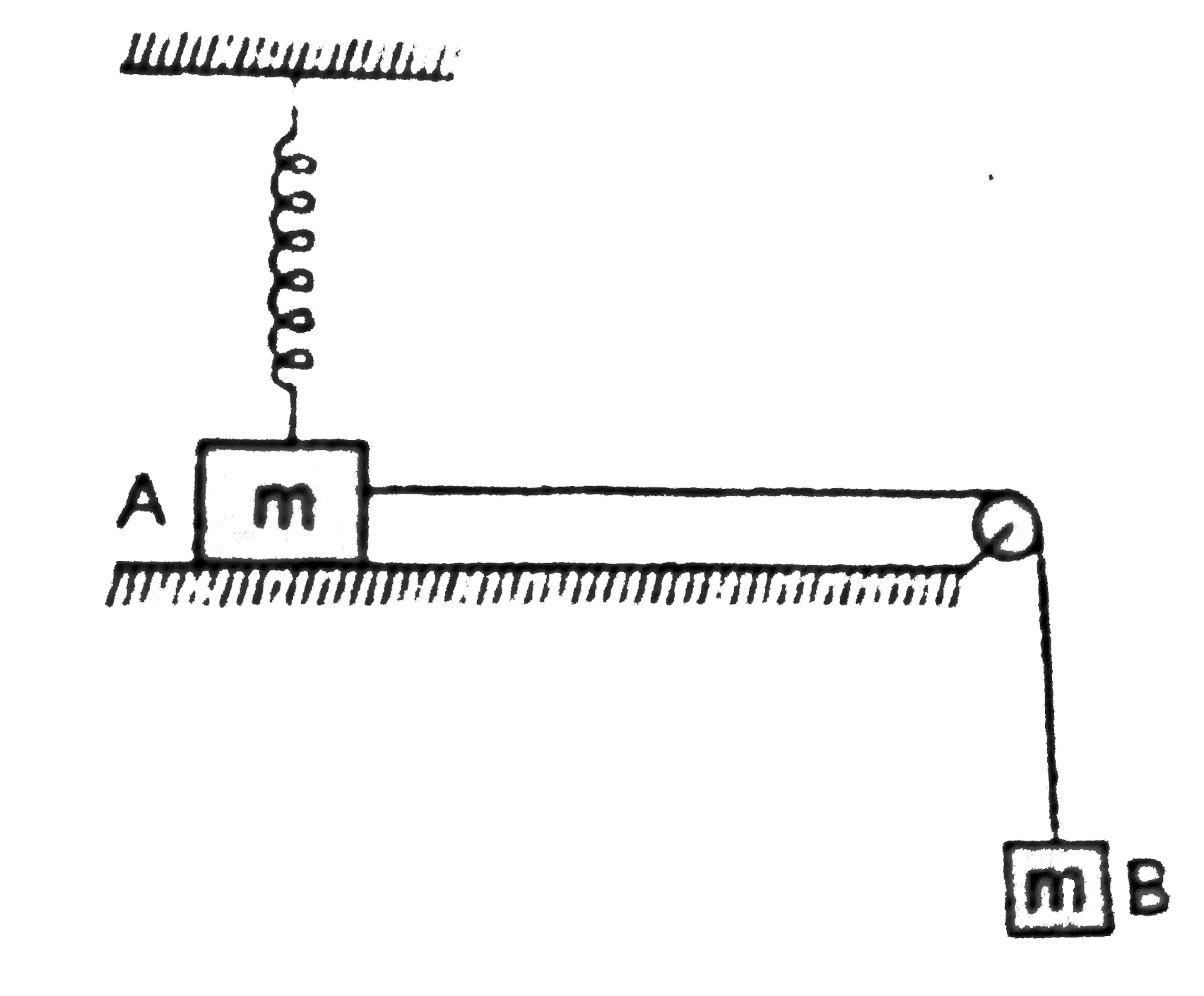
View SolutionFigure shows two block A and B, each having a mass of 320 g connected by a light string passing over a smooth light pulley. The horizontal surface on which the block A can slide is smooth. The block A is attached to spring constant 40N/m whose other end is fixed to a support 40 cm above the horizontal surface. Initially, the spring is vertical and unstretched when the system is released to move. Find the velocity of the block A at the instant it breaks off the surface below it. Take g=10m/s2 .
View SolutionIn fig.block A and B are connected together by a string and placed on a smooth inclined plane. B is connected to C(which is suspended vertically) by another string which passes over a smooth pulley fixed to th plane. The mass A is mA=1 kg and mass of B is mB=2kg.

(a) If the system is at rest, find the mass of C.
(b) If the mass of C is twice the mass calculate in (a) then find the acceleration of the system.
View SolutionTwo masses m1 and m2(m2>m1) are hanging vertically over frictionless pulley. The acceleration of the two masses is :

View SolutionTwo masses m1 and m2(m2>m1) are hanging vertically over frictionless pulley. The acceleration of the two masses is :

View SolutionA block of mass M is placed on a rough horizontal surface. It is connected by means of a light inextensible string passing over a smooth pulley . The other end of string passing over a smooth pulley. The other end of string is connected to a block of mass m. There is no friction between vertical surface and block m
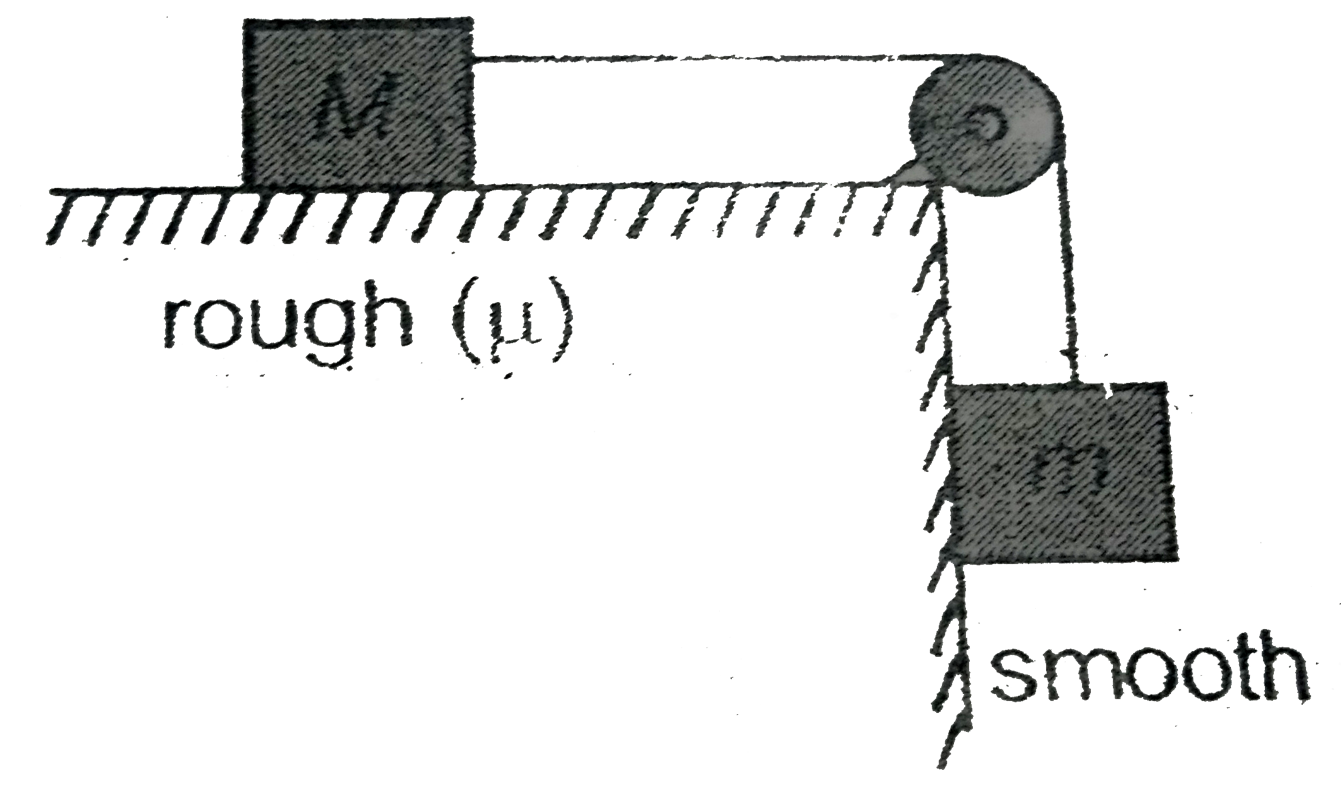
If the whole system ( horizontal surface + blocks ) accelerates towards right the value of maximum on the horizontal surface is
View Solution