A man, of mass 60kg, is riding in a lift. The weights of the man, when the lift is acceleration upwards and downwards at 2ms−2 are respectively.
(Taking g=10ms−2)
720 N and 480N
480N and 720N
600N and 600N
None of these
The correct Answer is:A
To solve the problem, we need to calculate the apparent weight of a man in a lift that is accelerating both upwards and downwards. The apparent weight is given by the normal force exerted by the weighing machine, which can be calculated using Newton's second law of motion.
Given:
- Mass of the man, m=60kg
- Acceleration due to gravity, g=10m/s2
- Acceleration of the lift, a=2m/s2
Step 1: Calculate the weight of the man
The weight of the man (force due to gravity) is given by:
W=m⋅g=60kg⋅10m/s2=600N
Step 2: Case 1 - Lift accelerating upwards
When the lift accelerates upwards, the apparent weight (normal force N) can be calculated using the equation:
N=W+m⋅a
Substituting the values:
N=600N+(60kg⋅2m/s2)=600N+120N=720N
Step 3: Case 2 - Lift accelerating downwards
When the lift accelerates downwards, the apparent weight can be calculated using the equation:
N=W−m⋅a
Substituting the values:
N=600N−(60kg⋅2m/s2)=600N−120N=480N
Final Results:
- Apparent weight when the lift accelerates upwards: 720 N
- Apparent weight when the lift accelerates downwards: 480 N
Summary:
- When the lift accelerates upwards, the man feels heavier, and his weight is 720 N.
- When the lift accelerates downwards, the man feels lighter, and his weight is 480 N.
- Mass of the man, m=60kg
- Acceleration due to gravity, g=10m/s2
- Acceleration of the lift, a=2m/s2
The weight of the man (force due to gravity) is given by:
W=m⋅g=60kg⋅10m/s2=600N
When the lift accelerates upwards, the apparent weight (normal force N) can be calculated using the equation:
N=W+m⋅a
Substituting the values:
N=600N+(60kg⋅2m/s2)=600N+120N=720N
When the lift accelerates downwards, the apparent weight can be calculated using the equation:
N=W−m⋅a
Substituting the values:
N=600N−(60kg⋅2m/s2)=600N−120N=480N
- Apparent weight when the lift accelerates upwards: 720 N
- Apparent weight when the lift accelerates downwards: 480 N
- When the lift accelerates upwards, the man feels heavier, and his weight is 720 N.
- When the lift accelerates downwards, the man feels lighter, and his weight is 480 N.
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBook:ALLENChapter:NEWTONS LAWS OF MOTIONExercise:EXERCISE-II
Explore 112 Videos
- NEWTONS LAWS OF MOTIONBook:ALLENChapter:NEWTONS LAWS OF MOTIONExercise:EXERCISE-III
Explore 28 Videos
- NEWTONS LAWS OF MOTIONBook:ALLENChapter:NEWTONS LAWS OF MOTIONExercise:SWOE
Explore 44 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBook:ALLENChapter:NEWTON'S LAWS OF MOTION & FRICTIONExercise:EXERCISE (JA)
Explore 4 Videos
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
Explore 24 Videos
Similar Questions
Knowledge Check
Two masses of 5 kg and 3 kg are suspended with the help of massless inextensible strings as shown in figure. The whole system is going upwards with an acceleration of 2ms−2. The tensions T1andT(2) are respectively (Take g=10ms−2)
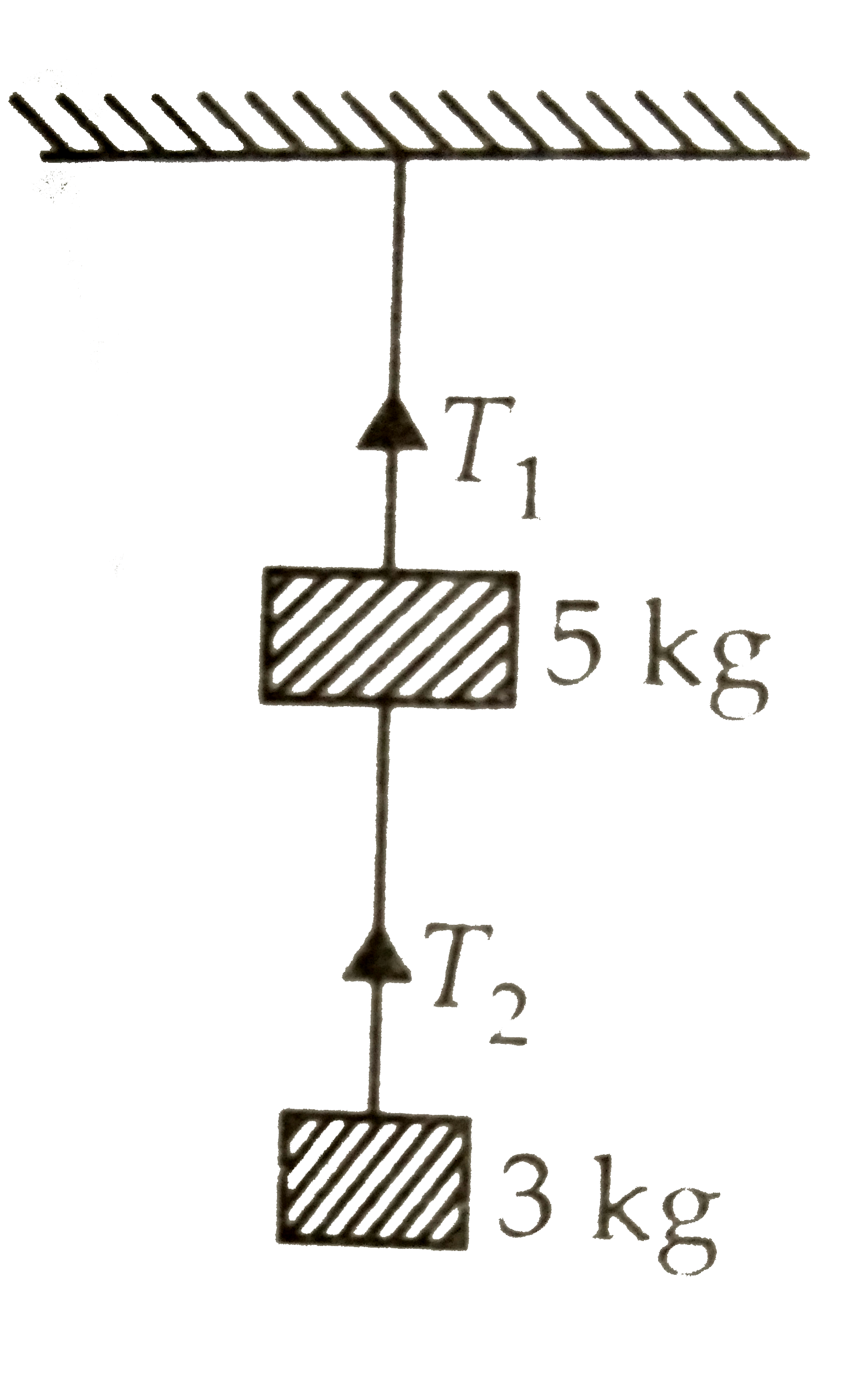 A96N, 36NB36N,96NC96N,96ND36N,36N
A96N, 36NB36N,96NC96N,96ND36N,36N
A man of 60kg mass is in a lift. Find the apparent weight of the man when the lift is moving (a) up with uniform acceleration 4ms−2 (b) down with uniform acceleration of 2ms−2 (g=10ms−2)
View SolutionA man of mass 60 kg is in a lift and lift is accelerating upwards with acceleration 4m/s2. Calculate effective weight of man in lift.
View SolutionHow does the weight of a person standing in a lift change when the lift accelerates (a) upwards (b) downwards with an acceleration a ?
View SolutionA body of mass 50 kg is hung by a spring balance in a lift. Calculate the reading of the balance when :
The lift is ascending with an acceleration of 2m/s2.
View SolutionA 75kg man stands in a lift. What force does the floor exert on him when the elevator starts moving upward with an acceleration of 2ms−2 Given: g = 10ms−2.
View SolutionA man of mass 60 kg is standing on a horizontal conveyor belt. When the belt is given an acceleration of 1ms−2, the man remains stationary with respect to the moving belt. If g=10ms−2, The net force acting on the man is

View SolutionA man of mass 60 kg records his weight on a weighing machine placed inside a lift . The ratio of the weights of the man recorded when the lift is ascending up with a uniform speed of 2 m/s to when it is descending down with a uniform speed of 4 m/s will be
View Solution