In Newton's second →F=m→a (for constant mass m), →a is the acceleration of the mass m with respect to
any observer
any inertial observer
an observer at rest only
an observer moving with uniform speed only
The correct Answer is:C
To solve the question regarding Newton's second law of motion, we need to understand the concept of acceleration in relation to the frame of reference. Here’s a step-by-step breakdown of the solution:
Step 1: Understanding Newton's Second Law
Newton's second law states that the net force acting on an object is equal to the mass of the object multiplied by its acceleration. Mathematically, this is expressed as:
→F=m→a
where:
- →F is the net force,
- m is the mass of the object,
- →a is the acceleration of the object.
Step 2: Identifying the Frame of Reference
The acceleration →a is defined with respect to a specific frame of reference. For Newton's laws to hold true, this frame must be an inertial frame of reference. An inertial frame is one that is not accelerating, meaning that it is either at rest or moving at a constant velocity.
Step 3: Implications of Non-Inertial Frames
If the frame of reference is non-inertial (accelerating), the application of Newton's second law becomes more complex. In such frames, fictitious forces (like centrifugal force or Coriolis force) may need to be introduced to account for the acceleration of the frame itself.
Step 4: Conclusion
Thus, to answer the question, the acceleration →a in Newton's second law is the acceleration of the mass m with respect to an inertial frame of reference. This means that the laws are valid only when observed from a frame that is not accelerating.
Final Answer
The acceleration →a in Newton's second law →F=m→a is the acceleration of the mass m with respect to an inertial frame of reference.
---
Newton's second law states that the net force acting on an object is equal to the mass of the object multiplied by its acceleration. Mathematically, this is expressed as:
→F=m→a
where:
- →F is the net force,
- m is the mass of the object,
- →a is the acceleration of the object.
The acceleration →a is defined with respect to a specific frame of reference. For Newton's laws to hold true, this frame must be an inertial frame of reference. An inertial frame is one that is not accelerating, meaning that it is either at rest or moving at a constant velocity.
If the frame of reference is non-inertial (accelerating), the application of Newton's second law becomes more complex. In such frames, fictitious forces (like centrifugal force or Coriolis force) may need to be introduced to account for the acceleration of the frame itself.
Thus, to answer the question, the acceleration →a in Newton's second law is the acceleration of the mass m with respect to an inertial frame of reference. This means that the laws are valid only when observed from a frame that is not accelerating.
The acceleration →a in Newton's second law →F=m→a is the acceleration of the mass m with respect to an inertial frame of reference.
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBook:ALLENChapter:NEWTONS LAWS OF MOTIONExercise:EXERCISE-II
Explore 112 Videos
- NEWTONS LAWS OF MOTIONBook:ALLENChapter:NEWTONS LAWS OF MOTIONExercise:EXERCISE-III
Explore 28 Videos
- NEWTONS LAWS OF MOTIONBook:ALLENChapter:NEWTONS LAWS OF MOTIONExercise:SWOE
Explore 44 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBook:ALLENChapter:NEWTON'S LAWS OF MOTION & FRICTIONExercise:EXERCISE (JA)
Explore 4 Videos
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
Explore 24 Videos
Similar Questions
Knowledge Check
A rocket of initial mass 6000kg ejects mass at a constant rate of 16kg/s with constant relative speed of 11m/s What is the acceleration of the rocket one mnute after blast ?
A25ms−2B50ms−2C10ms−2D35ms−2
A body A mass m1 exerts a force on another body B of mass m2 . If the acceleration of B be a2 , then the acceleration (in magnitude) of A is
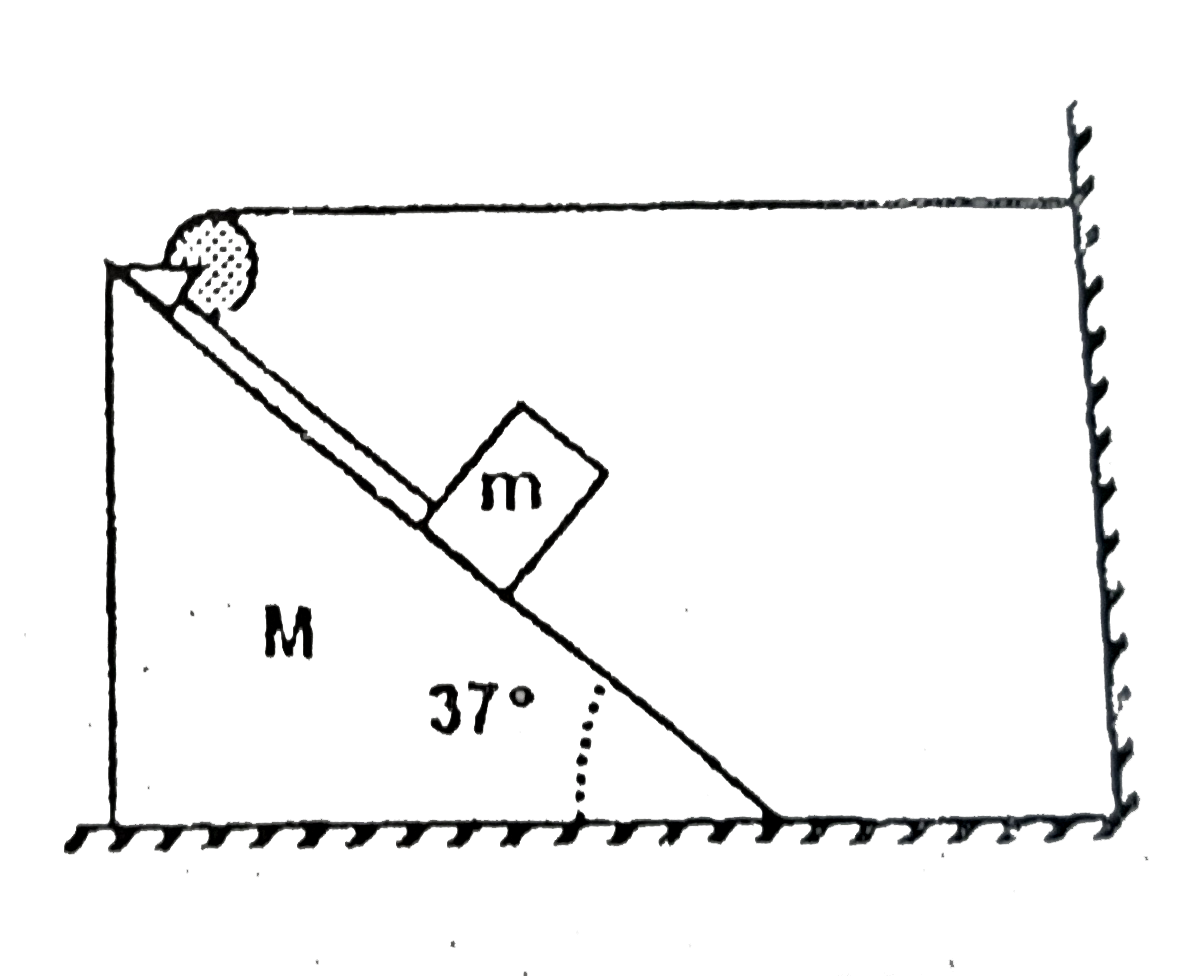
View SolutionA block of mass m=5kg is placed on the wedge of mass M=32kg as shown in the figure. Find the acceleration of wedge with respect to ground. (Neglect any type of friction. Spring and pulley are ideal)
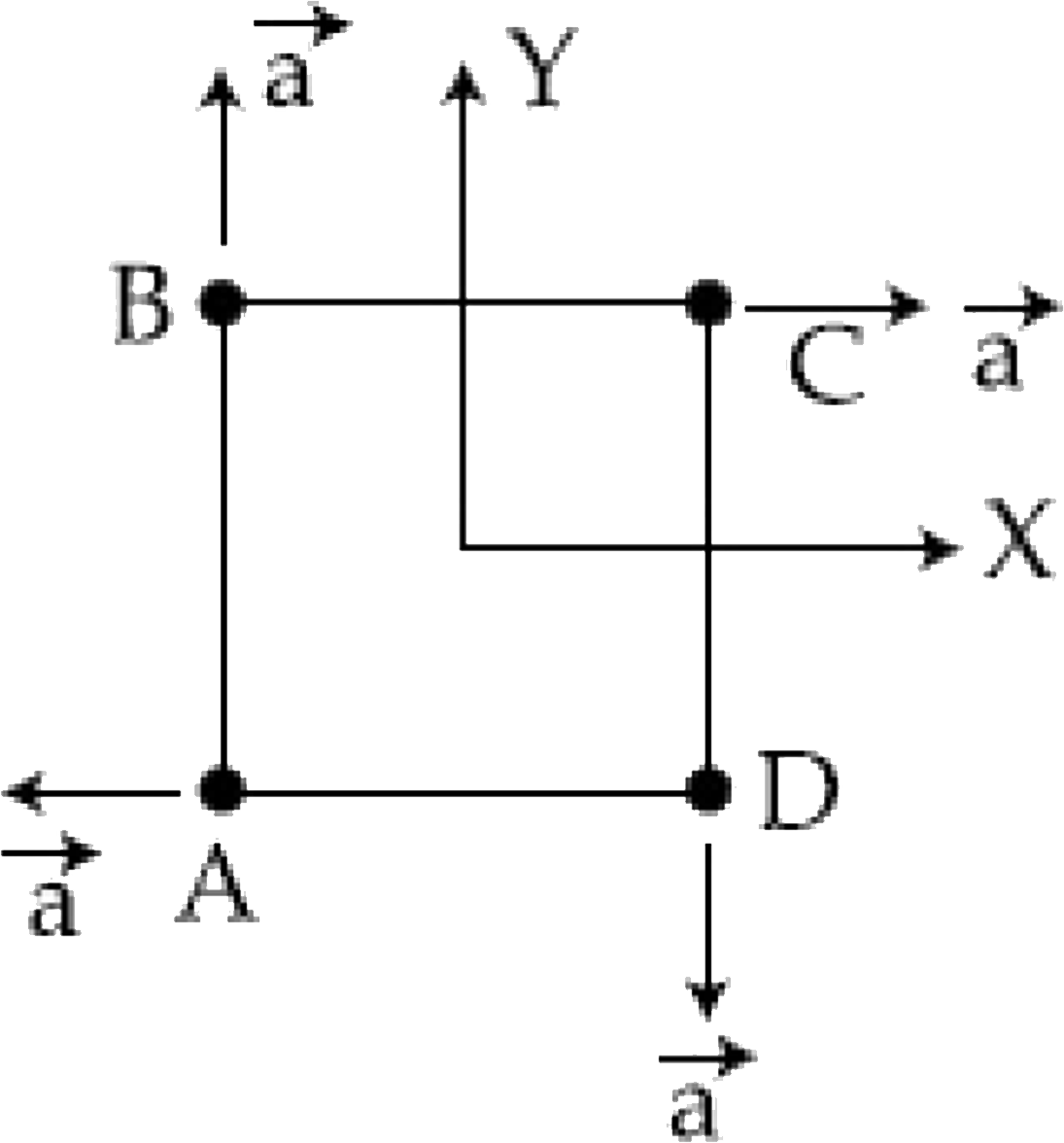
View SolutionFour particles A,B,C and D with masses mA=m,mB=2m,mC=3m and mD=4m are at the comers of a square. They have accelerations of equal magnitude with directions as shown. The acceleration of the centre of mass of the particles is :
View Solution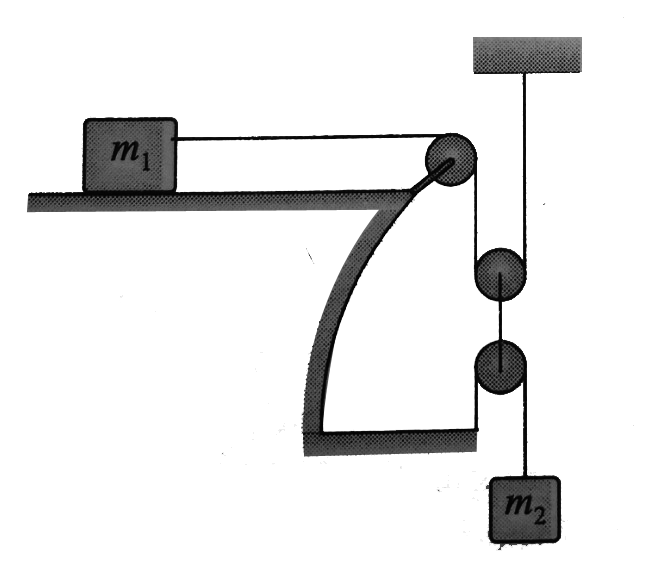
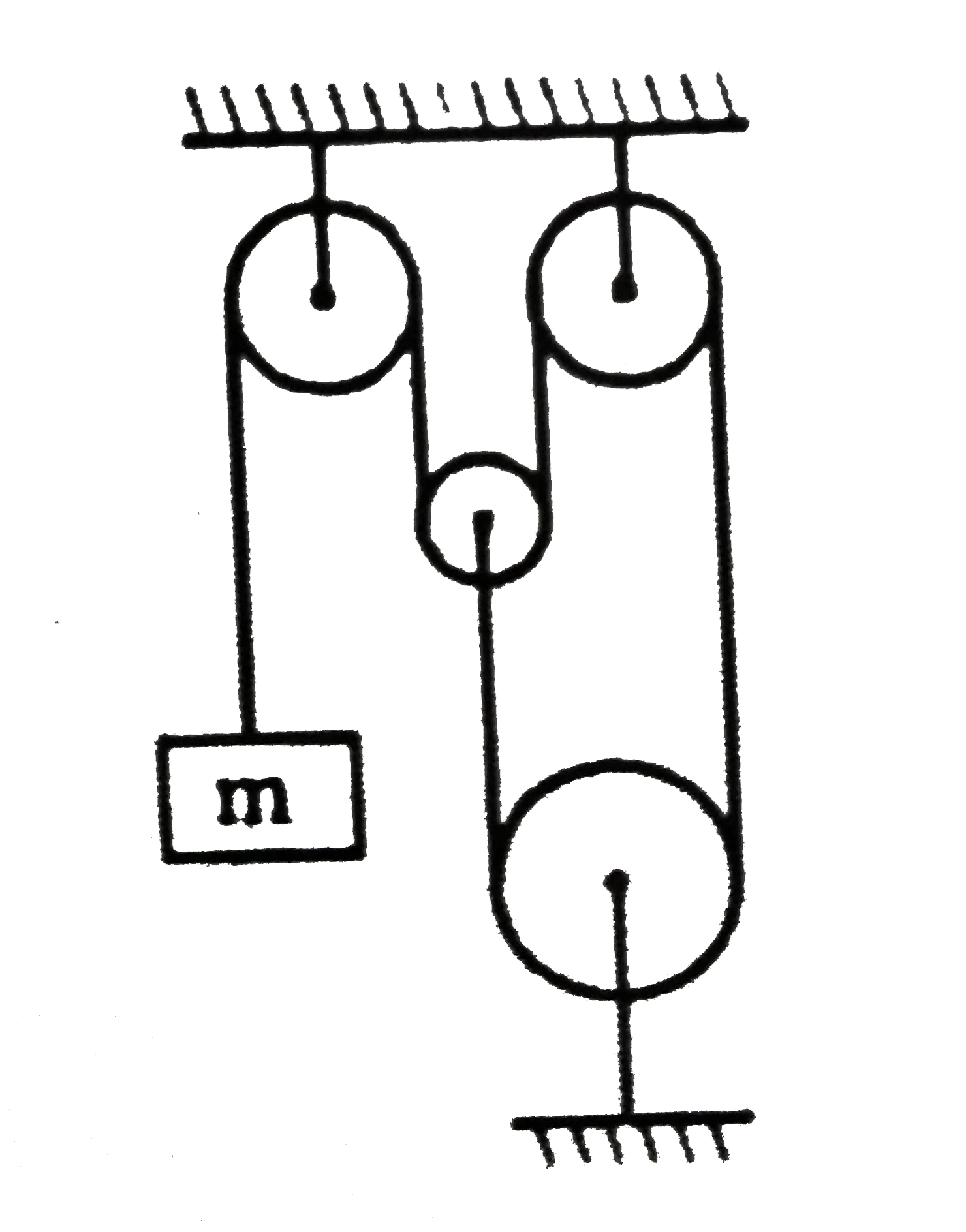
Two blocks of masses m1 and m2 are connected as shown in the figure. The acceleration of the block m2 is :
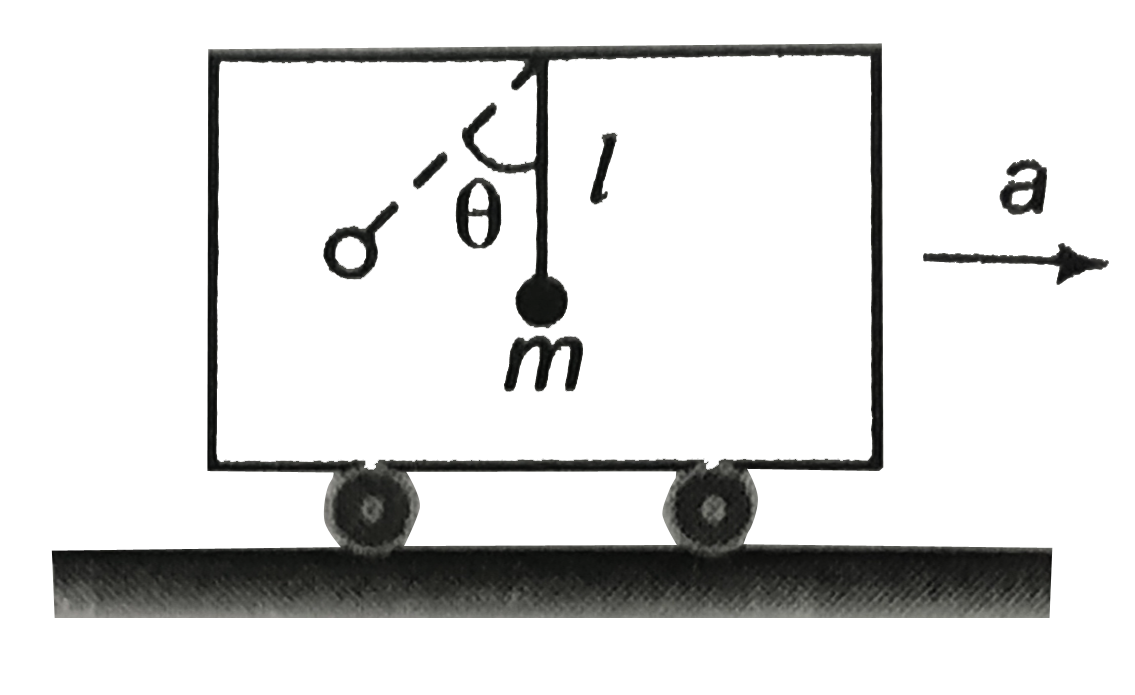
View SolutionA body of mass M is moving in +x-direction with acceleration a. Find the minimum value of μ so that a body of mass m can be held stationary with respect to M, on the vertical side of M.
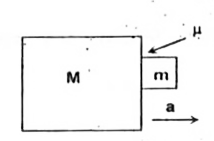
View SolutionA particle of mass m is thrown horizontally from the top of a tower and anoher particle of mass 2m is thrown vertically upward. The acceleration of centre of mass is
View SolutionA particle of mass m is thrown horizontally from the top of a tower and anoher particle of mass 2m is thrown vertically upward. The acceleration of centre of mass is
View Solution