Find the impulse experienced by a body.If the body mass M hits normally a rigid wall with velocity v and bounces back with the same speed.
MV
1.2 MV
2 MV
Zero
The correct Answer is:C
To find the impulse experienced by a body of mass M that hits a rigid wall with velocity v and bounces back with the same speed, we can follow these steps:
Step 1: Understand the Initial and Final Momentum
When the body hits the wall, its initial momentum pinitial can be calculated as:
pinitial=M⋅v
where v is the velocity of the body before hitting the wall.
Step 2: Calculate the Final Momentum
After bouncing back, the body moves in the opposite direction with the same speed. Thus, the final momentum pfinal is:
pfinal=M⋅(−v)=−M⋅v
The negative sign indicates that the direction of the velocity has reversed.
Step 3: Calculate the Change in Momentum
The impulse experienced by the body is equal to the change in momentum, which can be expressed as:
Impulse=pfinal−pinitial
Substituting the values from Step 1 and Step 2, we get:
Impulse=(−M⋅v)−(M⋅v)
Impulse=−M⋅v−M⋅v=−2M⋅v
Step 4: Interpret the Result
The impulse experienced by the body is −2M⋅v. The negative sign indicates that the impulse is in the opposite direction to the initial motion of the body.
Final Answer
Thus, the impulse experienced by the body is:
Impulse=2M⋅v
When the body hits the wall, its initial momentum pinitial can be calculated as:
pinitial=M⋅v
where v is the velocity of the body before hitting the wall.
After bouncing back, the body moves in the opposite direction with the same speed. Thus, the final momentum pfinal is:
pfinal=M⋅(−v)=−M⋅v
The negative sign indicates that the direction of the velocity has reversed.
The impulse experienced by the body is equal to the change in momentum, which can be expressed as:
Impulse=pfinal−pinitial
Substituting the values from Step 1 and Step 2, we get:
Impulse=(−M⋅v)−(M⋅v)
Impulse=−M⋅v−M⋅v=−2M⋅v
The impulse experienced by the body is −2M⋅v. The negative sign indicates that the impulse is in the opposite direction to the initial motion of the body.
Thus, the impulse experienced by the body is:
Impulse=2M⋅v
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBook:ALLENChapter:NEWTONS LAWS OF MOTIONExercise:EXERCISE-II
Explore 112 Videos
- NEWTONS LAWS OF MOTIONBook:ALLENChapter:NEWTONS LAWS OF MOTIONExercise:EXERCISE-III
Explore 28 Videos
- NEWTONS LAWS OF MOTIONBook:ALLENChapter:NEWTONS LAWS OF MOTIONExercise:SWOE
Explore 44 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBook:ALLENChapter:NEWTON'S LAWS OF MOTION & FRICTIONExercise:EXERCISE (JA)
Explore 4 Videos
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
Explore 24 Videos
Similar Questions
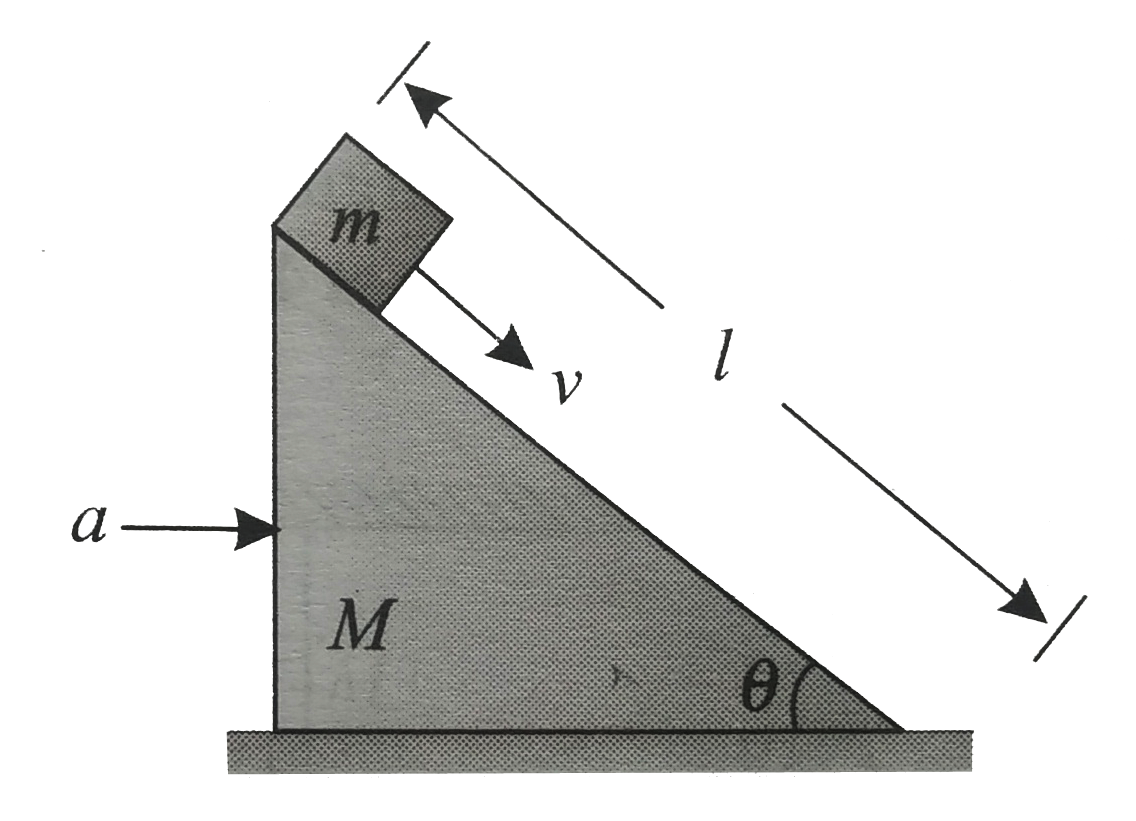
A smooth wedge of mass M is pushed with an acceleration a=>anθ and a block of mass m is projected down the slant with a velocity v relative to the wedge.
The horizontal force applied on the wedge is:
View SolutionA body of mass m collides against a wall with the velocity v and rebounds with the same speed. Its magnitude of change of momentum is
View Solution
Knowledge Check
The linear momentum of a body of mass m moving with velocity v is :
Av/mBm/vCmvD1/mvA ball of mass m strikes a rigid walJ with speed u and rebounds with the same speed. The impulse imparted to the ball by the wall is
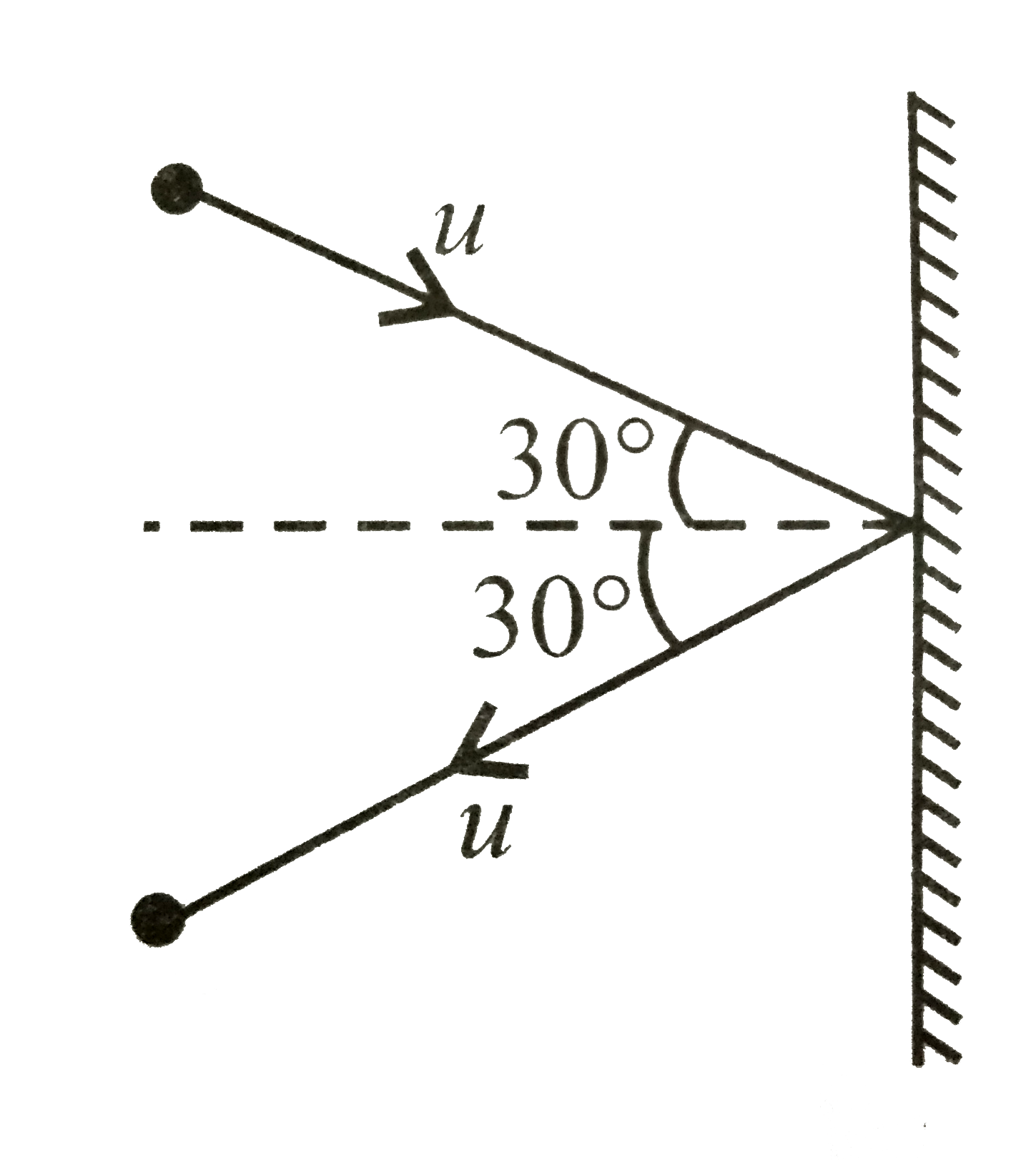 Amu sin30∘tB2mu sin30∘tCmu cos30∘tD2mu cos30∘t
Amu sin30∘tB2mu sin30∘tCmu cos30∘tD2mu cos30∘tA ball of mass m strikes a rigid walJ with speed u and rebounds with the same speed. The impulse imparted to the ball by the wall is
A2muBmuCzeroD−2mu
A ball hits a vertical wall horizontal at 10 m/s bounces back at 10 m/s
View SolutionA spherical ball of mass 10−6 kg hits a wall 1000 times per second normally with a velocity of 1000 m/s and rebounds with same velocity along the initial direction. The force experienced by the wall is
View SolutionA metal ball hits a wall and does not rebound whereas a rubber ball of the same mass on hitting the wall the same velocity rebounds back. It can be concluded that–
View SolutionFind the work done by the wall in reflecting the particle if the particle of mass m is moving horizontally with a constant velocity v towards a rigid wall that is moving in opposite direction with a constant speed u. Assuming elastic impact between the particle and wall
View SolutionA ball of mass 0.5kg moving with a velocity of 2m/s strikes a wall normally and bounces back with the same speed . If the time of contact between the ball and the wall is 1 millisecond , the average force exerted by the wall on the ball is
View Solution

