A 75kg man stands in a lift. What force does the floor exert on him when the elevator starts moving upward with an acceleration of 2ms−2 Given: g = 10ms−2.
To solve the problem of finding the force exerted by the floor on a 75 kg man in an elevator accelerating upwards at 2ms², we can follow these steps:
Step 1: Identify the forces acting on the man
When the elevator is moving upwards, two main forces act on the man:
1. The gravitational force (weight) acting downwards, which is given by Fg=mg.
2. The normal force (the force exerted by the floor on the man), which acts upwards.
Step 2: Calculate the weight of the man
The weight of the man can be calculated using the formula:
Fg=mg
Where:
- m=75kg (mass of the man)
- g=10m/s2 (acceleration due to gravity)
Calculating the weight:
Fg=75kg×10m/s2=750N
Step 3: Apply Newton's second law
When the elevator accelerates upwards, the net force acting on the man can be expressed using Newton's second law:
Fnet=ma
Where:
- a=2m/s2 (acceleration of the elevator)
The net force is also the difference between the normal force N and the weight Fg:
Fnet=N−Fg
Step 4: Set up the equation
Combining these equations, we have:
N−Fg=ma
Substituting Fg and rearranging gives:
N=Fg+ma
Step 5: Substitute the values
Now we can substitute the values into the equation:
N=750N+(75kg×2m/s2)
Calculating the additional force due to acceleration:
75kg×2m/s2=150N
Step 6: Calculate the normal force
Now, substituting back we get:
N=750N+150N=900N
Final Answer
The force that the floor exerts on the man when the elevator starts moving upward is 900N.
---
When the elevator is moving upwards, two main forces act on the man:
1. The gravitational force (weight) acting downwards, which is given by Fg=mg.
2. The normal force (the force exerted by the floor on the man), which acts upwards.
The weight of the man can be calculated using the formula:
Fg=mg
Where:
- m=75kg (mass of the man)
- g=10m/s2 (acceleration due to gravity)
Fg=75kg×10m/s2=750N
When the elevator accelerates upwards, the net force acting on the man can be expressed using Newton's second law:
Fnet=ma
Where:
- a=2m/s2 (acceleration of the elevator)
Fnet=N−Fg
Combining these equations, we have:
N−Fg=ma
Substituting Fg and rearranging gives:
N=Fg+ma
Now we can substitute the values into the equation:
N=750N+(75kg×2m/s2)
Calculating the additional force due to acceleration:
75kg×2m/s2=150N
Now, substituting back we get:
N=750N+150N=900N
The force that the floor exerts on the man when the elevator starts moving upward is 900N.
Similar Questions
In a given figure the acceleration of M is (g=10ms−2)

View SolutionThe mass of man when standing on the lift is 60 kg. The weight when the lift is moving upwards with acceration 4.9ms−2 is
View SolutionA man of mass 40kg is standing on a weighting machine kept on the floor of an elevator which is moving up with an acceleration of 2m/s2 Find the reading of the weighing maching.

View SolutionA man of mass 40kg is standing on a weighting machine kept on the floor of an elevator which is moving up with an acceleration of 2m/s2 Find the reading of the weighing maching.

View SolutionCalculate the work done in lifting a 300N weight to a height of 10m with an acceleration 0.5ms−2. Take g=10ms−2.
View SolutionWhat normal force does the floor of an elevator exert on a 90 kg person if the person / elevator system accelerates upward at 1m/s2 ?
View SolutionA man of 60kg mass is in a lift. Find the apparent weight of the man when the lift is moving (a) up with uniform acceleration 4ms−2 (b) down with uniform acceleration of 2ms−2 (g=10ms−2)
View SolutionFind the acceleration of 3kg mass when acceleration of 2kg mass is ms−2 as shwon in fig.
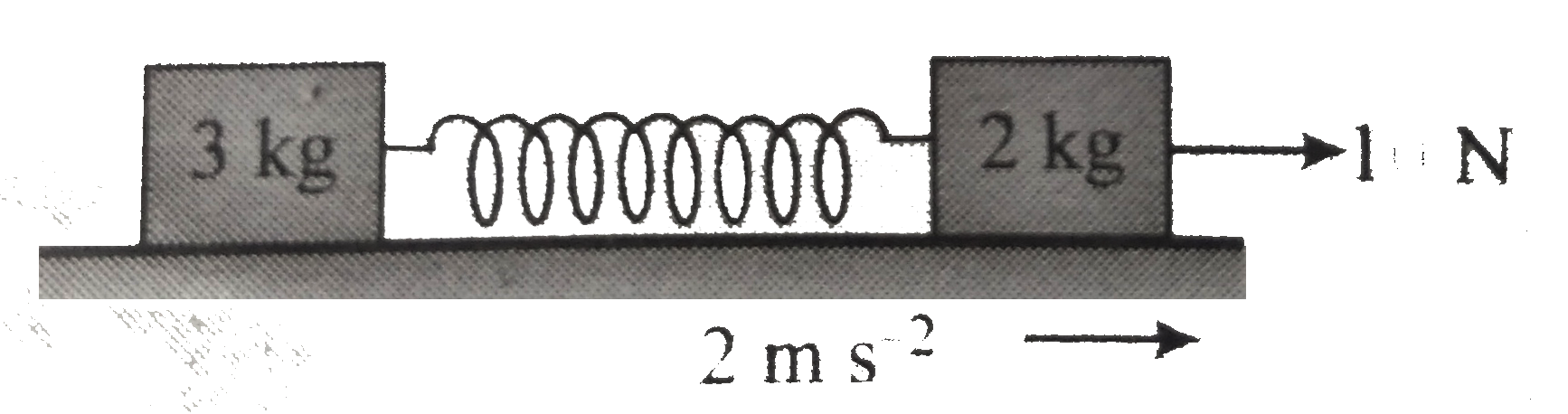
View SolutionA man is standing on a weighing machine placed in a lift. When stationary his weight is recorded as 40 kg . If the lift is accelerated upwards with an acceleration of 2m/s2 , then the weight recorded in the machine will be (g=10m/s2)
View SolutionA man, of mass 60kg, is riding in a lift. The weights of the man, when the lift is acceleration upwards and downwards at 2ms−2 are respectively.
(Taking g=10ms−2)
View Solution

